引用本文
张建山, 刘建新, 郝丽, 张君子, 孔维韬, 张成武, 张文雅. 气测曲线峰型形态定量化评价方法及其应用实例[J]. 录井工程, 2020,31(1): 12-18.
ZHANG Jianshan, LIU Jianxin, HAO Li, ZHANG Junzi, KONG Weitao, ZHANG Chengwu, ZHANG Wenya. Quantitative evaluation method of peak configuration of gas logging curve and application example[J]. Mud Logging Engineering, 2020,31(1): 12-18.
Doi:10.3969/j.issn.1672-9803.2020.01.003  
Permissions
Copyright©2020, 《录井工程》杂志社
《录井工程》杂志社 所有
气测曲线峰型形态定量化评价方法及其应用实例
张建山, 刘建新, 郝丽, 张君子, 孔维韬, 张成武, 张文雅
中国石油渤海钻探工程有限公司第二录井分公司

作者简介：张建山 工程师,1987年生,2014年毕业于中国石油大学(华东)油气田开发工程专业,现从事地质综合研究相关工作。通信地址:062552 河北省任丘市渤海钻探工程有限公司第二录井分公司地质研究评价中心。电话:(0317)2701479。E-mail:upczhjsh@126.com

摘要

气测曲线峰型形态特征可以反映储集层流体在纵向上的差异,能够有效判别储集层流体性质。但目前还不能实现定量化评价,指导意义受限。将余弦相似度原理引入到气测曲线峰型形态定量化评价中,选取不同流体类型的标准峰型形态作为原型计算余弦相似度,对每种峰型的相似度赋以不同权重系数,通过综合计算得出“峰型指数”,可以有效对气测曲线峰型形态进行定量化评价;进一步将“峰型指数”与气测全烃值特征参数、气测组分值特征参数结合构建三维解释图板,发现不同性质流体区分效果明显。经过实际应用验证可知,综合解释吻合率为82.6%(与试油结论对比),能够满足生产需求。

关键词: 气测解释; 峰型形态; 峰型指数; 余弦相似度; 定量化评价; 三维图板
中图分类号:TE132.1 文献标志码:A
Quantitative evaluation method of peak configuration of gas logging curve and application example
ZHANG Jianshan, LIU Jianxin, HAO Li, ZHANG Junzi, KONG Weitao, ZHANG Chengwu, ZHANG Wenya
No.2 Mud Logging Company, BHDC, CNPC, Renqiu, Hebei 062552, China
Abstract

The configuration characteristics of the peak shape of the gas logging curve can reflect the vertical difference of reservoir fluid, and can effectively discriminate the fluid properties of the reservoirs. But the quantitative evaluation cannot be realized at present, and the guiding significance is limited. The cosine similarity principle is introduced into the quantitative evaluation of peak configuration of gas logging curve. By selecting the configuration of the standard peak shape of different fluid types as the prototype to calculate the cosine similarity, the similarity of each peak shape is assigned with different weight coefficients, and the peak shape index is obtained by comprehensive calculation, which can effectively carry out quantitative evaluation on the configuration the peak shape of gas logging curve. Furthermore, the peak shape index was combined with the characteristic parameters of total hydrocarbon value and component value of gas logging to construct the three-dimensional interpretation chart, it is found that the boundaries of different fluid properties are obvious. It is proved by practical application that the coincidence rate of comprehensive interpretation is 82.6%(compared with the conclusion of well test), which can meet the production demands.

Keyword: gas logging interpretation; the configuration of the peak shape; peak shape index; cosine similarity; quantitative evaluation; the three-dimensional chart
0 引 言

气测录井的连续性、灵敏性优势非常明显[1], 可对钻井过程中返出钻井液中的烃类气体含量进行连续监测, 获取气测全烃值、气测组分值、全烃曲线峰型形态等信息[2], 有效反映储集层的含油气情况[3]。应用气测全烃值、气测组分值及其派生参数已能够实现定量化评价, 以此为基础建立的三角形图板解释方法、皮克斯勒图板解释方法、相对比值图板解释方法、气体湿度图板解释方法等提高了气测解释的准确性、时效性[4, 5], 并大幅降低了人为主观因素造成的不确定性。然而, 全烃曲线峰型形态信息的应用仍然停留在人工识别阶段, 完全依靠人为主观判断来定性评价, 不仅效率低下, 而且影响因素过多, 不同解释评价者、不同曲线比例尺等都会影响判断结果, 因此应用效果受到很大限制。本文首次将曲线余弦相似度原理引入全烃曲线峰型形态的评价中, 通过选取不同流体类型的标准峰型作为计算原型, 对每种峰型赋以不同权重值, 综合计算得出“ 峰型指数” , 最终实现对峰型形态的定量化评价, 以达到更好的应用效果。

1 余弦相似度基本原理

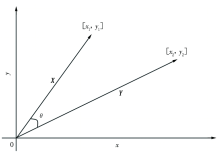
余弦相似度[6]又称余弦相似性。空间中两个向量存在一定夹角, 夹角越小说明指向越相近, 相似度也就越高。因此, 可以利用该夹角的余弦值大小来判别这两个向量的相似性。例如, 在二维坐标系中, 坐标分别为[x1, y1]、[x2, y2]的两个向量X、Y, 它们之间的夹角为θ , 如图1所示。

图1 二维向量夹角示意图

根据余弦定理, 可以计算两个向量X、Y间夹角θ 的余弦值为:

cosθ = x1x2+y1y2x12+y12×x22+y22(1)

余弦取值为-1~1。如果cosθ =1, 则两者相似度为1, 说明这两个向量之间的夹角为0° , 指向完全相同, 相似度最好; 如果cosθ =0, 则相似度为0, 两个向量之间的夹角为90° , 指向垂直, 相似度一般; 如果cosθ =-1, 则相似度为-1, 两个向量之间的夹角为180° , 指向完全相反, 相似度最差。

余弦相似度也可以用于判别两个多维向量之间的相似性[7]。假定空间中存在两个n维向量, 其夹角为θ , 其中向量A为[a1, a2, …, an], 向量B为[b1, b2, …, bn], 则两个多维向量夹角的余弦值为:

cos(A, B)= ∑i=1n(ai×bi)∑i=1nai2×∑i=1nbi2(2)

同理, 可利用n维向量夹角的余弦值来判别这两个向量之间的相似性。需要说明的是, 当向量起点为0时, 余弦相似度仅仅与两个向量的变化趋向有关, 而与它们的绝对值大小无关。例如, 向量A为[0, 1, 2, 3, 4, 5], 向量B为[0, 2, 4, 6, 8, 10], 尽管两个向量的绝对值不同, 但其变化趋向完全一致, 表明二者相似度为1。

气测曲线由一系列与深度值相对应的全烃值数据组成, 某一井段内的气测曲线全烃值可视为一个n维向量。通过与标准曲线对比, 计算两者之间的余弦相似度, 便可以判断二者的相似程度, 因此利用余弦相似度进行气测曲线峰型形态的定量化评价是可行的。

2 利用余弦相似度计算峰型指数
2.1 概念的引入

气测曲线不同的峰型形态代表储集层流体在纵向上的差异。通常, 气测峰型越饱满、均匀, 含油的可能性越大, 即两者之间呈正相关性。基于两者之间的这种相关性, 为了更加明确地反映储集层流体的这种特性, 本文引入“ 峰型指数” 的概念。

“ 峰型指数” 主要依据余弦相似度来计算。但是, 如果直接将余弦相似度作为“ 峰型指数” , 计算结果必然不够精确, 因为不同性质流体有着不同的峰型, 而且不同形状的峰型可能具有相同的余弦相似度。为此, 必须选取不同类型流体的标准峰型作为计算原型, 并对其他每种峰型赋以不同权重系数, 经综合计算求得其“ 峰型指数” 。

2.2 典型峰型形态特征

总结饶阳凹陷肃宁-大王庄构造带东营组地层中油层、油水同层、含油水层气测曲线峰型形态特征, 选取最典型峰型作为标准峰型, 如图2所示。

图2 饶阳凹陷肃宁-大王庄构造带不同流体性质气测曲线峰型形态特征

油层:全烃曲线形态为饱满型。全烃值上升速度快、幅度大, 之后趋于平直, 最后回落到基值, 气测异常厚度与储集层厚度相当, 峰型跨度较大, 峰型饱满, 形如一“ 箱体” 。

油水同层:全烃曲线形态为欠饱满型。与油层形态不同的是, 气测异常厚度比储集层厚度要小, 高点位于曲线中上部, 回落相对较慢。

含油水层:全烃曲线形态为倒三角形。曲线前沿上升快, 后沿回落缓慢, 呈明显“ 拖尾” 现象, 高点在上部。

需要说明的是, 在此之所以未考虑标准水层的峰型形态, 是因为水层气测异常普遍较低甚至无异常, 计算结果代表性差。

2.3 对典型峰型形态进行数字化赋值

仅仅依靠曲线形态无法进行数学计算, 需对每种典型峰型形态进行数字化赋值。在赋值过程中, 由于不同井段井深、厚度、全烃值差异较大, 在此必须进行归一化处理:将深度数值归一为0~10 m, 全烃最高值归一为10%, 依此统一标准, 建立11维空间如表1所示。其中, 不同峰型归一化后向量值分别为:

油层:A油层=[0, 8.1, 9.7, 10, 10, 10, 10, 10, 9.7, 8.1, 0]

油水同层:A油水同层=[0, 8.1, 9.7, 10, 9.7, 7.5, 5, 2.5, 1.25, 0.5, 0]

含油水层:A含油水层=[0, 8.1, 10, 6.25, 3.1, 1.9, 1.25, 0.75, 0.4, 0.2, 0]

表1 不同典型峰型归一化数值
2.4 划分气测异常井段

根据实际气测全烃数据、测井数据及岩性数据, 划分气测异常层段。对于井深数值, 必须进行差值处理, 地层厚度归一为10 m, 以达到与标准峰型数值统一为11维空间。对于全烃数值, 由前面的分析可知, 两个向量起点为0时, 余弦相似度与两个向量的绝对值大小无关, 因此无须归一化, 但需要扣除基值, 以便达到向量起点为0, 与标准峰型起点一致。例如, 某井在井段3 364~3 372 m见气测异常, 此时地层厚度为8 m, 全烃值有9个数值, 与标准峰型不一致, 因此必须进行差值计算, 达到11维空间。归一化后气测数值如表2所示。气测异常井段归一化后的全烃向量值为:

B=[0, 2.608, 4.892, 5.812, 4.864, 2.08, 1.008, 0.41, 0.142, 0.06, 0.02]

表2 某井归一化后数据
2.5 计算峰型指数

利用归一化后的全烃数值, 根据余弦相似度原理分别计算该层段与标准油层、标准油水同层、标准含油水层的余弦相似度, 记为cos(θ )油层、cos(θ )油水同层、cos(θ )含油水层。

最后, 计算该层段峰型指数:

Kf=φ 油层× cos(θ )油层+φ 油水同层× cos(θ )油水同层+φ 含油水层× cos(θ )含油水层 (3)

cos(θ )油层=cos(A油层, B)(4)

cos(θ )油水同层=cos(A油水同层, B) (5)

cos(θ )含油水层=cos(A含油同层, B)(6)

式中:φ 油层为油层权重系数, 肃宁-大王庄构造带取100; φ 油水同层为油水同层权重系数, 肃宁-大王庄构造带取40; φ 含油水层为含油水层权重系数, 肃宁-大王庄构造带取5; cos(θ )油层为与标准油层峰型形态的余弦相似度; cos(θ )油水同层为与标准油水同层峰型形态的余弦相似度; cos(θ )含油水层为与标准含油水层峰型形态的余弦相似度。

余弦相似度计算结果如下:油层为0.77, 油水同层为0.96, 含油水层为0.88; 峰型指数为119.8。对于权重系数, 不同地区取值不同, 遵循的原则是:油层取值最高, 油水同层次之, 含油水层取值最低。所以, 越接近油层峰型指数就会越高, 越接近含油水层峰型指数就会越低。

3 建立三维解释图板

虽然峰型指数为解释油气水层提供了非常重要的依据, 但仅仅依靠峰型指数还不能满足生产需求, 必须结合其他气测参数进行综合评价。由前面的分析可知, 气测录井的有效信息可分为3类, 即气测全烃值信息、气测组分值信息、全烃曲线峰型形态信息, 因此将这3类特征参数分别作为X、Y、Z坐标轴, 建立三维立体解释图板。

统计饶阳凹陷肃宁-大王庄构造带东营组地层近几年共计52口井、73个试油层的试油、气测数据, 以其中50层作为源数据进行分析研究, 以另外23层用于验证。首先, 总结饶阳凹陷肃宁-大王庄构造带不同流体类型的气测响应特征。

油层:气测值较高, 多数大于2%; 组分齐全, C1相对含量相对较低, 多数介于50%~75%之间, C3/C2比值普遍大于1.2; 全烃曲线形态为饱满型, 峰型指数普遍大于130。

油水同层:气测值低于油层, 多数介于1%~7.5%之间; 组分较为齐全, C1相对含量略高于油层, 多数在60%~85%之间, C3/C2比值普遍介于1.0~1.5之间; 全烃曲线形态为欠饱满型, 峰型指数普遍介于125~135之间。

水层、含油水层:气测值较低, 多数小于3%; 组分不齐全, C1相对含量较高, 多数大于75%, C3/C2比值普遍小于1.2; 全烃曲线形态分为两种情况, 一是气测值几乎无异常, 二是存在明显气测异常, 但全烃曲线形态为倒三角形, 峰型指数小于125。

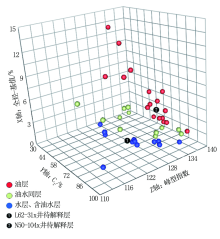
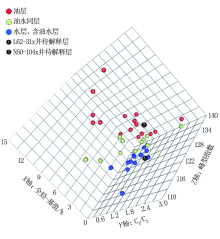
以此为依据构建三维解释图板, 其中:X轴为全烃值特征, 在此取全烃值与基值的差值; Y轴为气测组分值特征, 在此取C1相对百分含量值或C3与C2相对百分含量比值; Z轴为全烃曲线峰型形态特征, 在此取峰型指数。用以上3类参数分别作为坐标轴, 构建三维气测解释图板(图3、图4)。从这两幅图板可以看出, 不同性质流体之间区分效果好, 分界较为明显。

图3 全烃基值、C1、峰型指数三维解释图板

图4 全烃基值、C3/C2、峰型指数三维解释图板

4 应用效果分析

以该区23层试油数据作为验证层来进行应用效果分析, 综合吻合率为82.6%(表3), 能够满足生产需求。以L 62-31x井、N 50-104x井为例, 对应用效果进行分析说明。

表3 应用效果分析统计
4.1 L 62-31x井

L 62-31x井是部署在饶阳凹陷大王庄油田L 62断块的一口开发井, 实钻过程中在东营组2 915~2 920 m井段见到良好油气显示(图5)。该井段全烃、组分值数据特征(表4)介于油水同层、含油水层之间, 仅靠全烃、组分数据难以区分。通过计算, 峰型指数为124.58(表3), 符合含油水层特征, 三维解释图板均位于水层、含油水层区域(图3、图4), 因此综合解释为含油水层。对相应井段进行试油, 采用抽汲方式, 产油0.1 m3/d, 产水13.59 m3/d; 累计产油0.96 m3, 累计产水104.92 m3, 证实为含油水层。

图5 L 62-31x井录井综合图

表4 L 62-31x井气测异常数据
4.2 N 50-104x井

N 50-104x井是部署在饶阳凹陷肃宁油田N 9断块的一口开发井, 实钻过程中在东营组3 259~3 268 m井段见到良好油气显示(图6、表5)。该井段峰型形状介于饱满、欠饱满之间, 主观上难以判定。通过计算, 峰型指数为134.04(表3), 呈油层特征, 三维解释图板位于油层区域(图3、图4), 综合解释为油层。

图6 N 50-104x井录井综合图

表5 N 50-104x井气测异常数据

相应井段直接投产, 产油11.8 m3/m, 无产水, 证实为油层。

5 结论与建议

全烃曲线形态特征可以有效反映储集层流体信息, 但其应用仍然停留在人工识别阶段, 无法实现定量化评价。

本文将余弦相似度原理引入到气测曲线峰型形态的判别中, 选取不同类型流体的标准峰型作为计算原型, 并对每种峰型赋以不同权重系数, 综合计算得出“ 峰型指数” ; 进一步将“ 峰型指数” 与气测全烃、组分数据结合, 构建三维气测解释图板, 可以有效判别流体性质。通过实际应用验证可知, 其效果良好, 能够满足生产需求。

“ 峰型指数” 的提出与应用, 有效解决了气测曲线无法定量化评价的难题, 提高了评价精度与效率。然而, 这仅仅是气测曲线定量化评价的首次尝试, 还需要进行后续研究来进一步完善。对于下步研究方向, 笔者有以下建议:

(1) 综合应用多种评价方法。评价曲线相似度的方法多种多样, 例如弗雷歇距离法、欧氏距离法、皮尔逊系数法等, 每种评价方法都具有各自的优缺点, 将这些方法综合运用, 可以取得更好的评价效果。

(2) 与气测值校正方法相结合。气测值的影响因素较多, 如钻时、钻井液参数等, 这些因素往往产生非真实的气测曲线形态。这种情况下, 首先需要对气测值进行校正, 在此基础上进行形态评价。

(3) 应用深度学习算法进行曲线识别。当前图像识别、人脸识别技术发展迅速, 与之相比, 气测曲线形态简单, 更易于识别与判断。利用计算机对曲线进行处理, 在此基础上加入气测解释相关理论进行分析, 利于达到自动评价的目的。

(编辑 姜萍)

参考文献
[1] 宋立春. 油气层录井的精细解释方法——以吉林探区为例[J]. 世界地质, 2009, 28(1): 92-97.
SONG Lichun. Precise logging interpretation methods for oil and gas layer in Jilin prospecting area[J]. Global Geology, 2009, 28(1): 92-97. [本文引用:1]
[2] 吴思仪, 司马立强, 袁龙, 等. 苏北盆地致密砂岩油藏气测录井评价方法[J]. 录井工程, 2014, 25(3): 41-45.
WU Siyi, SIMA Liqiang, YUAN Long, et al. Gas logging evaluation method for tight sand stone reservoirs in Subei Basin[J]. Mud Logging Engineering, 2014, 25(3): 41-45. [本文引用:1]
[3] 方锡贤, 程岩, 熊玉芹, 等. P2井特殊烃组分气测异常显示层探讨[J]. 录井工程, 2006, 17(1): 43-46.
FANG Xixian, CHENG Yan, XIONG Yuqin, et al. Discussion on gas logging abnormal show zone with the special hydrocarbon components in P2 well[J]. Mud Logging Engineering, 2006, 17(1): 43-46. [本文引用:1]
[4] 王斌, 张达清, 谌飞雁, 等. 彩南地区气测解释交汇图版的研制与应用[J]. 录井工程, 2005, 16(1): 9-12.
WANG Bin, ZHANG Daqing, SHEN Feiyan, et al. Development and application of intersection chart for gas logging interpretation in Cainan area[J]. Mud Logging Engineering, 2005, 16(1): 9-12. [本文引用:1]
[5] 吴文明, 杨瑞宝, 李雪瑞, 等. 红台地区西山窑组低饱和度油气藏气测解释评价方法[J]. 录井工程, 2017, 28(2): 89-94.
WU Wenming, YANG Ruibao, LI Xuerui, et al. Gas logging interpretation and evaluation method for low-saturation reservoirs of Xishanyao Formation in Hongtai area[J]. Mud Logging Engineerin, 2017, 28(2): 89-94. [本文引用:1]
[6] Wen C L, Wang Y C, Xu X B. Fuzzy information fusion algorithm of fault diagnosis based on similarity measure of evidence[M]∥Advances in Neural Networks - ISNN 2008. Springer Berlin Heidelberg, 2008. [本文引用:1]
[7] LAHITANI A R, PERMANASARI A E, SETIAWAN N A . Cosine similarity to determine similarity measure: Study case in online essay assessment[C]∥2016 4th International Conference on Cyber and IT Service Management. IEEE, 2016: 205-210. [本文引用:1]