引用本文
胡廷惠, 刘东, 于登飞, 付蓉, 章威.底水稠油油藏水平井生产规律实验研究及应用[J]. 录井工程, 2020,31(1): 132-138.
HU Tinghui, LIU Dong, YU Dengfei, FU Rong, ZHANG Wei. Experimental study and application of horizontal well production law in heavy oil reservoirs with bottom water[J]. Mud Logging Engineering, 2020,31(1): 132-138.
Doi:10.3969/j.issn.1672-9803.2020.01.024  
Permissions
Copyright©2020, 《录井工程》杂志社
《录井工程》杂志社 所有
底水稠油油藏水平井生产规律实验研究及应用
胡廷惠, 刘东, 于登飞, 付蓉, 章威
中海石油(中国)有限公司天津分公司

作者简介：胡廷惠 工程师,1985年生,2010年硕士毕业于中国石油大学(北京),现主要从事海上油田提高采收率技术的实施工作。通信地址:300459 天津市滨海新区海川路2121号渤海石油管理大厦A座1811室。电话:15822675948。E-mail:huth2@cnooc.com.cn

基金: “十三五”国家科技重大专项“渤海油田高效开发示范工程”(编号:2016ZX05058)
摘要

针对底水稠油油藏水平井开发油水运动复杂,高含水期生产时间长,后期调整挖潜困难的问题,开展了底水稠油油藏不同影响因素的油水运动规律和水平井生产特征研究。研发了物理模拟实验装置,并以渤海Q底水稠油油藏为原型,利用相似原理,开展三种不同粘度的原油在不同压差条件下进行水驱油的物理模拟实验,测定了产油量、产水量、含水率等参数随时间的变化关系,对比分析了不同生产压差、原油粘度时见水时间、无水期采收率、含水率上升速度等油田开发关键参数的变化规律。现场利用实验成果实施水驱,可提高采收率12%,该成果可用于指导底水稠油油藏优化水平井注采井网、注采井距以及合理生产压差指标选择。

关键词: 稠油; 水平井; 水驱规律; 生产压差
中图分类号:TE132.1 文献标志码:A
Experimental study and application of horizontal well production law in heavy oil reservoirs with bottom water
HU Tinghui, LIU Dong, YU Dengfei, FU Rong, ZHANG Wei
Tianjin Branch of CNOOC(China) Co., Ltd.,Tianjin 300459, China
Abstract

Aiming at the problems of complex oil-water movement, long production time in high water-cut periods, and difficulty in adjusting and tapping potential in later stages in the development of horizontal wells in heavy oil reservoirs with bottom water, the oil-water movement laws of different influencing factors in heavy oil reservoirs with bottom water and horizontal well production characteristics were studied. A physical simulation experimental apparatus was developed. Taking Bohai Q heavy oil reservoir with bottom water as a prototype, physical simulation experiments of water flooding of three types of crude oil with different viscosity under different pressure differences were carried out by using similar principles, and changes in parameters such as oil production, water production rate and water cut with time were measured. Variation law of the key parameters of oilfield development such as water breakthrough time, breakthrough recovery, and ascending velocity of water cut in different producing pressure difference and oil viscosity were comparatively analyzed. Water flooding on site with the experimental results can increase the recovery efficiency by 12%. The results can be used to guide the optimization of indexes of injection-production pattern, producer-injector spacing and reasonable differential pressure of production for horizontal wells in heavy oil reservoirs with bottom water.

Keyword: heavy oil; horizontal well; water flooding law; differential pressure of production
0 引 言

研究和实践表明, 底水油藏在国内外油田中分布广泛, 借助水平井可有效开发底水油藏, 其中油水运动规律研究是关键[1, 2, 3]。主要原因在于水平井与油藏接触面积大, 因而渗流阻力小, 可降低底水的锥进速度, 延长无水采油期, 从而提高油井的产量和采收率[4, 5, 6, 7]。目前, 底水稠油油藏的见水机理和规律的研究仍然是一个难题, 普遍认为水平井合理生产压差的确定和防堵水更是困难[8, 9, 10, 11, 12]。很多学者对该类油藏的油井产能及水锥特性展开了大量研究, 但由于底水锥进问题定解条件的非线性, 使得该问题难以进行解析求解[13, 14, 15, 16, 17, 18, 19, 20]。目前对于水平井多是将三维问题转化为二维平面问题处理, 直井则多利用等值渗流阻力法将油藏中流体的流动划分为符合不同流动规律的流动区域, 然后利用各流动区域所符合的流动规律进行近似计算[21, 22]。无论水平井和直井, 都缺乏底水稠油油藏水驱油机理的实验资料。

为直观地反映底水稠油油藏油水运动规律和水平井生产特征, 研发了底水稠油油藏水平井物理模拟实验装置, 并以渤海Q底水稠油油藏为原型, 利用相似原理, 对不同粘度的模拟原油在不同压差条件下进行水驱油的物理模拟实验, 探索影响底水稠油油藏生产关键参数的变化规律, 以期为该类油藏的科学开发提供借鉴和指导。

1 物理模拟实验设计
1.1 实验装置

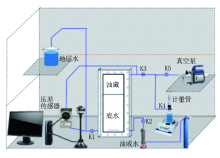
整套实验装置主要由平板油藏模型、氮气瓶、真空泵、水源、压力传感器、天平、油水分离计量装置、计算机及数据自动采集系统组成(图1)。平板油藏模型是可视的, 在实验过程可以用相机实时观测并记录驱替现象的变化, 以及观察底水稠油油藏水平井开发的见水规律。

图1 底水油藏水驱实验装置

1.2 相似准则生产压差研究

相似准则是物理模拟的基础, 通过一系列的相似准数(表1)可以将油田现场的单井模型按比例转换为能在实验室进行实验的小模型, 并使物理实验结果更加可信。相似准则研究基本假设如下:(1)油藏水平等厚; (2)油藏中的流体流动过程按油、水两相处理, 且油水不相容; (3)整个开采过程为等温开采; (4)油水粘度保持不变; (5)渗流介质为多孔介质, 且具有各向同性; (6)流体在油藏中的流动满足达西定律。井距、原油密度、重力加速度相似准数分别为694.444、1.047、1。

表1 相似准则参数

根据相似准则以及油田实际的生产压差, 计算出实验室条件下与之对应的压差, 并验证相似准数, 具体参数见表2。

表2 不同压差相似准则参数

表2说明本实验模型的生产压差满足相似准则, 实现了油田现场原型与物理模型之间生产压差的相互换算。渤海Q底水稠油油藏水平井生产压差范围0.4~2.5 MPa, 注采井距250~300 m。实验中选取不同生产压差(0.8、1.0、1.2、1.5、2.0、3.0、5.0 MPa)进行研究, 由此计算得到压力梯度最大为5 MPa/250 m(即0.02 MPa/m), 用此压力梯度计算得到实验室条件下的最大注采驱替压差约为0.02 MPa/m× 0.36 m(即0.007 2 MPa)。

1.3 实验步骤

水驱油实验有稳态法和非稳态法两种。稳态法通过测量稳态驱替下的压差和流量, 并直接用达西公式计算出相对渗透率曲线, 因此其结果精确度主要取决于实验过程的稳定性和参数计量的精确性。稳态法的优点是精确度高, 最大的缺点是测量周期太长。非稳态法的实验时间比较短, 流体的流动过程与实际油藏基本相同, 因此采用非稳态法进行水驱油实验。

实验步骤:(1)连接好装置, 如图1所示, 计量管倒放(里面盛水), 开启压差传感器及数据采集系统; (2)放置好天平, 天平通电15 min后, 在天平上放置干净的烧杯; (3)用水头压力来测试和校正压差传感器, 确定不同水头压力对应的驱替压差(压差传感器量程选用要对应), 其值为4.4、4.7、5.0、5.4、6.1、7.5、10.3 kPa; (4)利用水头压力, 将水注入模型, 打开阀门K1、K3、K4, 关闭K5, 开始水驱油实验; (5)调节驱替压差至指定值, 待其稳定后, 油进入计量管时, 确定起始时刻; (6)需读取数据包括:时间、天平读数、计量管油水界面读数、驱替压差; (7)从起始时刻开始, 根据计量管中油水界面的变化(初期变化大, 后期变化小, 记录间隔为2 mL), 确定记录时间, 反复读数, 注意出口管线中的液体, 当出现一个水滴时, 记录其进入计量管的时刻, 即为见水时间, 见水后根据产油量, 按需加密记录, 直至油水界面不变化; (8)含水率达到98%的时候, 测定残余油条件下不同流速时水相有效渗透率; (9)稳定时间间隔, 记录天平读数, 驱替压差; (10)连续测量三次, 相对误差小于3%; (11)撤离计量管与天平上的烧杯; (12)实验结束, 关闭阀门K2、K3、K4。

2 实验结果与分析
2.1 渗透率的影响

图2是渗透率为2.82× 103 mD时水驱油的饱和度图(红色为原油, 白色为水, 水平井部署在模型底部)。由图2可知, 水驱油过程以平行推进为主, 见水时间长, 无水采收率高。

图2 渗透率为2.82× 103 mD时水驱油饱和度

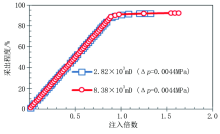
图3是原油粘度为22 mPa· s且生产压差为0.004 4 MPa时, 渗透率为2.82× 103 mD与8.38× 103 mD的采出程度与注入倍数的关系曲线。由图3可知, 在不同渗透率下, 采出程度与注入倍数的关系曲线重合, 可见水驱油实验对渗透率并不敏感, 所以后续的实验将采用渗透率2.82× 103 mD。

图3 不同渗透率条件下采出程度与注入倍数对比

2.2 生产井井型的影响

图4是粘度为74 mPa· s、压差为0.005 4 MPa时水平井与定向井注水的水驱油饱和度变化图(左为水平井注水, 右为定向井注水)。水平井注水与定向井注水都可见到锥进现象, 但定向井注水驱替见水时间更快。定向井注水时实验前期是从裂缝中间部分开始驱替, 见水后再向两边延伸驱替; 水平井注水时实验前期是先从两边开始驱替, 见水后再向中间延伸驱替。

图4 粘度为74 mPa· s时不同时刻水驱油饱和度

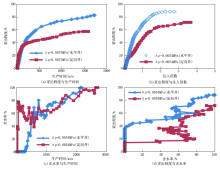
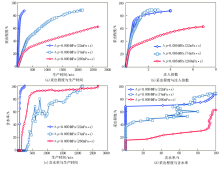
对水平井与定向井注水时粘度为74 mPa· s水驱油实验各七组不同压差下的数据进行对比与分析, 并计算与绘制七组实验采出程度与生产时间的关系曲线、采出程度与注入倍数的关系曲线、含水率与生产时间、采出程度与含水率的关系曲线, 如图5所示。由图5可知, 在相同压差下水平井注水驱替效率比定向井注水驱替效率高, 且在相同注入倍数下水平井注水驱替的采出程度比定向井要高, 而水平井注水驱替的含水率比定向井要低; 说明对粘度为74 mPa· s的底水稠油油藏, 水平井注水比定向井注水开发效果好。

图5 压差为0.005 4 MPa水平井与定向井生产曲线对比

2.3 生产压差的影响

当原油粘度为22 mPa· s时, 进行水平井注水不同压差下的水驱油实验, 发现压差为0.003 6、0.003 9、0.004 4、0.004 7、0.005 0、0.005 4 MPa时, 前期出现小范围的锥进现象, 后期以平行推进为主, 驱替效率较高; 而压差为0.006 1、0.007 5、0.010 3 MPa的水驱油实验, 整个驱替过程都有一定的锥进现象, 驱替效率比前几个压差实验的低(图6, 左为压差0.004 4 MPa, 右为压差0.006 1 MPa)。表3是原油粘度为22 mPa· s时, 不同压差下的水平井注水实验数据。由表3可知, 生产压差越小, 最终产油量越大, 无水采油期越长, 无水采收率越大, 产水量越小, 驱替效率越高; 说明在相同注入倍数下, 采出程度越高。

图6 粘度为22 mPa· s时不同时刻水驱油饱和度

表3 粘度为22 mPa· s水平井注水时不同压差下水驱油数据
2.4 原油粘度的影响

图7是22、74、260 mPa· s三个粘度在压差为0.005 4 MPa条件下进行水平井注水驱油的实验对比。可以看出, 当注入倍数小于1.5时, 粘度为260 mPa· s的采出程度最低, 粘度为22 mPa· s的采出程度最高; 当注入倍数超过1.5时, 粘度为260 mPa· s的采出程度最低, 粘度为74 mPa· s的采出程度最高。可见提高注入倍数可以提高稠油采出程度, 即在稠油油田通过增注提液等措施可以改善开发效果。

图7 压差为0.005 4 MPa不同粘度水平井注水生产曲线对比

3 矿场应用

渤海Q底水油藏油柱高度6~20 m, 储集层具有高孔、高渗的物性特征, 垂向韵律为正韵律; 地层原油粘度为22、74、260 mPa· s; 底水能量较强, 水体倍数为30~50倍。底水油藏调整前采用定向井开发, 综合含水率达90%左右, 采出程度仅10%。为了提高底水油藏的储量动用程度和水驱采收率, 根据实验研究成果, 开展了调整方案研究, 优化了水平井注采井距、注采井网以及水平井合理生产压差(表4), 并改善了开发效果, 采油速度由0.8%提高到1.5%, 水驱采收率由18%提高到30%。

表4 渤海Q底水油藏水平井布井参数优化结果与实施效果统计
4 结论与建议

通过相似准则, 实现了油田现场原型与物理模型之间生产压差的相互换算, 现场实践证明, 实验结果可有效指导生产。

(1)原油粘度为22 mPa· s水平井注水的驱替实验随着压差的增加, 见水时间越快, 无水期采收率越低; 原油粘度为74 mPa· s水平井与定向井注水的驱替实验在压差为0.005 4 MPa时见水时间最长, 无水采收率最高; 原油粘度为260 mPa· s水平井注水的驱替实验随着压差的增加, 见水时间越快, 无水采收率越低; 原油粘度为260 mPa· s定向井注水的驱替实验也是在压差为0.005 4 MPa时见水时间最长, 无水采收率最高。

(2)在同一压差下, 水平井注水驱替的实验粘度为22 mPa· s的无水采油期最长, 无水采收率最高; 实验粘度为260 mPa· s的无水采油期最短, 无水采收率最低; 定向井注水驱替的实验粘度为74 mPa· s的无水采油期比粘度为260 mPa· s的要长, 无水采收率要高。

(3)在同一粘度同一压差下, 水平井注水的见水时间比定向井注水更长, 无水采收率更高。

(编辑 棘嘉琪)

参考文献
[1] 李传亮. 油藏工程原理[M]. 北京: 石油工业出版社, 2005.
LI Chuanliang. Fundamentals of reservoir engineering[M]. Beijing: Petroleum Industry Press, 2005. [本文引用:1]
[2] 何鲁平, 陈素珍, 俞启泰. 底水驱油藏水平井数值模拟研究[J]. 大庆石油地质与开发, 1995, 14(2): 26-30.
HE Luping, CHEN Suzhen, YU Qitai. Numerical simulation of horizontal well in bottom water drive reservoir[J]. Petroleum Geology & Oilfield Development in Daqing, 1995, 14(2): 26-30. [本文引用:1]
[3] 陈明, 沈燕来, 杨寨. 底水油藏水平井合理位置的确定方法研究[J]. 西南石油学院学报, 2003, 25(6): 31-34.
CHEN Ming, SHEN Yanlai, YANG Zhai. Method of determining optimum well location for horizontal well in bottom-water reservoir[J]. Journal of Southwest Petroleum Institute, 2003, 25(6): 31-34. [本文引用:1]
[4] 何冠军. 底水油气藏的经营管理研究[D]. 成都: 西南石油学院, 2002.
HE Guanjun. Management research of bottom-water reservoir[D]. Chengdu: Southwest Petroleum Institute, 2002. [本文引用:1]
[5] 葛丽珍, 张鹏. 秦皇岛32-6 油田含水率上升快原因分析[J]. 中国海上油气, 2005, 17(6): 394-397.
GE Lizhen, ZHANG Peng. An analysis of causes for rapidly-increasing water cut in QHD32-6 oilfield[J]. China Offshore Oil and Gas, 2005, 17(6): 394-397. [本文引用:1]
[6] 孙召勃, 贾晓飞, 李彦来, 等. 有限水体底水油藏水平井压力动态分析模型[J]. 大庆石油地质与开发, 2018, 37(6): 49-53.
SUN Zhaobo, JIA Xiaofei, LI Yanlai, et al. Analyzing model of the pressure dyanmics of the horizontal well in the bottom-water oil reservoir with finite water bodies[J]. Petroleum Geology & Oilfield Development in Daqing, 2018, 37(6): 49-53. [本文引用:1]
[7] 赵燕, 陈向军. 底水油藏水锥回落高度预测模型[J]. 断块油气田, 2018, 25(3): 367-370.
ZHAO Yan, CHEN Xiangjun. Prediction models of water cone falling height for bottom water reservoirs[J]. Fault-Block Oil & Gas Field, 2018, 25(3): 367-370. [本文引用:1]
[8] 陈军, 刘太雷. 底水气藏气井水锥动态模拟及见水时间预测[J]. 大庆石油地质与开发, 2019, 38(1): 84-88.
CHEN Jun, LIU Tailei. Modeling of the water coning dynamics and the prediction of the water breakthrough time for the gas well in bottom-water gas reservoirs[J]. Petroleum Geology & Oilfield Development in Daqing, 2019, 38(1): 84-88. [本文引用:1]
[9] 侯亚伟. 基于动态数据的底水油藏水平井水脊增长模型[J]. 大庆石油地质与开发, 2018, 37(2): 79-82.
HOU Yawei. Growth model of the horizontal-well water crest in the bottom-water oil reservoir based on the dynamic data[J]. Petroleum Geology & Oilfield Development in Daqing, 2018, 37(2): 79-82. [本文引用:1]
[10] 蒋平, 张贵才, 何小娟, 等. 底水锥进的动态预测方法[J]. 钻采工艺, 2007, 30(2): 71-73.
JIANG Ping, ZHANG Guicai, HE Xiaojuan, et al. A dynamic prediction method for bottom water coning[J]. Drilling & Production Technology, 2007, 30(2): 71-73. [本文引用:1]
[11] 蒋平. 底水锥进预测及底水治理决策技术研究[D]. 东营: 中国石油大学(华东), 2006.
JIANG Ping. The study of prediction of water coning and decision-making technique for water shutoff for bottom-water reservoir[D]. Dongying: China University of Petroleum(east china), 2006. [本文引用:1]
[12] 唐人选. 底水油藏水锥动态模拟及见水时间预测[J]. 新疆石油地质, 2003, 24(6): 572-573.
TANG Renxuan. Simulation of water coning performance and prediction of water breakthrough time in bottom-water reservoirs[J]. Xinjiang Petroleum Geology, 2003, 24(6): 572-573. [本文引用:1]
[13] 李传亮. 水锥形状分析——与朱圣举先生商榷[J]. 新疆石油地质, 2002, 23(1): 74-75.
LI Chuanliang. Shape analysis of water coning: A discussion with Mr. Zhu Shengju[J]. Xinjiang Petroleum Geology, 2002, 23(1): 74-75. [本文引用:1]
[14] 侯君, 程林松. 常规底水油藏水锥高度计算方法研究[J]. 西安石油大学学报(自然科学版), 2006, 21(3): 23-26.
HOU Jun, CHENG Linsong. Calculation method for the water cone height of bottom-water reservoir[J]. Journal of Xi'An Shiyou University(Natural Science Edition), 2006, 21(3): 23-26. [本文引用:1]
[15] 谢林峰, 李相方. 底水气藏水锥高度与形状计算新方法[J]. 天然气工业, 2004, 24(4): 54-56.
XIE Linfeng, LI Xiangfang. New calculating method of highness and shape of water cone for gas pool driven by botton water[J]. Natural Gas Industry, 2004, 24(4): 54-56. [本文引用:1]
[16] 姜汉桥, 姚军, 姜瑞忠. 油藏工程原理与方法[M]. 东营: 石油大学出版社, 2003.
JIANG Hanqiao, YAO Jun, JIANG Ruizhong. Reservoir engineering principle and method[M]. Dongying: University of Petroleum Press, 2003. [本文引用:1]
[17] 李传亮. 修正DUPUIT 临界产量公式[J]. 石油勘探与开发, 1993, 20(4): 91-95.
LI Chuanliang. Correction DUPUIT critical production formula[J]. Petroleum Exploration and Development, 1993, 20(4): 91-95. [本文引用:1]
[18] 黄炳光, 刘蜀知. 实用油藏工程与动态分析方法[M]. 北京: 石油工业出版社, 1998.
HUANG Bingguang, LIU Shuzhi. Practical reservoir engineering and dynamic analysis method[M]. Beijing: Petroleum Industry Press, 1998. [本文引用:1]
[19] 窦宏恩. 水平井开采底水油藏临界产量的计算[J]. 石油钻采工艺, 1997, 19(3): 70-75.
DOU Hongen. Calculation of critical yield of bottom water reservoir in horizontal well production[J]. Oil Drilling & Production Technology, 1997, 19(3): 70-75. [本文引用:1]
[20] 程林松, 郎兆新, 张丽华. 底水驱油藏水平井锥进的油藏工程研究[J]. 石油大学学报(自然科学版), 1994, 18(4): 43-47.
CHENG Linsong, LANG Zhaoxin, ZHANG Lihua. Reservoir engineering research on horizontal well coning in bottom water drive reservoir[J]. Journal of the Univeristy of Petroleum(Natural Science Edition), 1994, 18(4): 43-47. [本文引用:1]
[21] 范子菲, 林志芳. 底水驱动油藏水平井临界产量公式及其变化规律研究[J]. 石油勘探与开发, 1994, 21(1): 65-70.
FAN Zifei, LIN Zhifang. Study on critical production formula of horizontal well in bottom water driven reservoir and its variation law[J]. Petroleum Exploration and Development, 1994, 21(1): 65-70. [本文引用:1]
[22] 朱圣举. 预测无隔板底水油藏油井见水时间的修正式[J]. 新疆石油地质, 1999, 18(3): 56-57, 75.
ZHU Shengju. A modified formula for predicting water breakthrough time of oil wells in bottom water reservoirs with no barrier[J]. Xinjiang Petroleum Geology, 1999, 18(3): 56-57, 75. [本文引用:1]