基于录井数据计算地层漏失压力的方法

引用本文

方俊伟, 杨涪杰, 贾晓斌, 邓明毅. 基于录井数据计算地层漏失压力的方法[J]. 录井工程, 2020,31(1): 7-11.
FANG Junwei, YANG Fujie, JIA Xiaobin, DENG Mingyi. Method of calculating formation leakage pressure based on mud logging data[J]. Mud Logging Engineering, 2020,31(1): 7-11.
Doi:10.3969/j.issn.1672-9803.2020.01.002 复制到剪切板

Permissions

《录井工程》杂志社所有

基于录井数据计算地层漏失压力的方法

方俊伟^①,^②, 杨涪杰^③, 贾晓斌^①,^②, 邓明毅^③

①中石化西北油田分公司石油工程技术研究院

②中国石化缝洞型油藏提高采收率重点实验室

③西南石油大学

作者简介：方俊伟副研究员,1986年生,2011年获西南石油大学海洋油气工程专业硕士学位,现在从事钻井完井液及储集层保护技术研究工作。通信地址:830011 新疆乌鲁木齐长春南路466号西北石油局。E-mail:fangjunwei555@126.com

基金: 中国石油化工股份有限公司重大科技项目群“顺北油气田一区优快钻井技术研究”(编号:P18021-2)

摘要

钻进过程中突发井漏会导致大量钻井液漏失,严重的会影响正常钻进周期甚至使整口井报废,因而提前确定易漏失层位的漏失压力并进行相应的钻井液密度设计是高效防漏堵漏作业的前提,同时也是同一区块其他井地质工程设计的重要依据。为此,研发了一种基于录井数据计算地层漏失压力的方法。首先构建一套判别模型,通过实钻录井数据对钻遇的致漏裂缝类型进行识别,然后基于统计法,结合现场收集的目标井的井漏数据,构建漏失压差与漏失流量的相关性,最后拟合求取地层漏失压力。现场应用表明,该方法可以有效地指导相关堵漏作业与钻井液密度设计,实例校验证明,应用该模型计算漏失压力优于传统的统计法。

关键词: 录井数据; 裂缝性地层; 砂泥岩混层; 漏失压力; 统计法

中图分类号:TE132.1 文献标志码:A

Method of calculating formation leakage pressure based on mud logging data

FANG Junwei^①,^②, YANG Fujie^③, JIA Xiaobin^①,^②, DENG Mingyi^③

①Sinopec Research Institute of Petroleum Engineering of Northwest Oilfield Company, Urumqi, Xinjiang 830011, China

②Sinopec Key Laboratory for EOR of Fractured-Vuggy Reservoirs, Urumqi, Xinjiang 830011, China

③Southwest Petroleum University, 610500, China

Abstract

Sudden lost circulation during drilling will cause vast loss of drilling fluid, which will seriously affect the normal drilling cycle and even make the whole well scrapped. Therefore, to determine the leakage pressure of lost-circulation zones, and to design the corresponding drilling fluid density in advance are preconditions for high efficient preventing and treating lost circulation, and they are also important bases for the geological engineering design of other wells in the same block. To this end, a method for calculating formation leakage pressure based on mud logging data has been developed. First, a set of discriminant models are constructed, and the types of fractures causing leakage during drilling are identified by mud logging data of actual drilling. Then, based on the statistical method and combined with the lost circulation data of the target well collected on site, the correlation between leakage pressure difference and leakoff flow rate is constructed. Finally, the formation leakage pressure is obtained by fitting. Field application shows that this method can effectively guide related dental work and drilling fluid density design. The verification of examples proved that application of this model to calculate the leakage pressure is superior to the traditional statistical method.

Keyword: mud logging data; fractured formation; sandstone and mudstone interbedding; leakage pressure; statistical method

文章图片

0 引言

井漏是钻井施工中的重大技术难题, 钻遇裂缝则是造成井漏的主要原因, 针对钻遇裂缝的相关研究有很多。1964年Drummond^[1]提出可利用天然裂缝性储集层的大量钻井液漏失资料来确定地层岩石孔隙度; 1988年 Pouisen^[2]基于钻井流体漏失形态呈线性并平行于裂缝面、流体漏失服从达西定理、漏失流体是不可压缩的和储集层是无限平行于裂缝面4个假设前提推导出了描述水力裂缝中流体漏失的通用公式; 1990年N.Morita^[3]提出了漏失压力理论, 分析了漏失压力影响因素; 1992年 Dyke等^[4]详细论述了钻井过程中的钻井液漏失响应, 对钻井液漏失控制给出了合理的建议; 2004年Alexandre Lavtov^[5]提出了裂缝性地层的漏失模型, 描述了钻井液在径向单裂缝中的漏失机理, 定量描述了钻井液实时漏失曲线; 同年, Lavtov^[6]等提出假设钻井液为幂律流体, 裂缝为有限长的平面圆盘状, 裂缝宽度随压力线性变化, 建立了单条裂缝的径向漏失模型; 2007年金衍等^[7]通过现场漏失井深、工况、发生率、漏失通道进行统计分析, 构建了统计法计算漏失压力的模型; 2008年朱亮等^[8]将统计法建立的漏失压力计算模型与力学计算模型进行了比较, 证明统计法要优于力学计算法。结合前人研究, 本文提出了一种基于录井数据的裂缝类型识别方法, 使用某区块的实钻资料对该方法的准确性进行校核。结果证明裂缝区分后计算的漏失压力的结果更符合现场实际, 并通过该方法建立了目标层的诱导裂缝地层漏失压力方程, 为该区块防漏堵漏提供了理论依据与数据支持。

1 基于录井参数的裂缝漏失压力理论分析

1.1 录井数据计算漏失流量

在钻井过程中, 因为存在自然渗漏和填充井中的新钻空间等不确定因素, 所以钻井液的出口流量一直是波动的(一般为进口流量的20%~30%)。这个特点导致现场只能通过对钻井液池液面变化的记录获得钻井液在一段时间内的总漏失量, 进而计算出漏失流量, 往往难以获得单次井漏过程中钻井液漏失流量的动态变化, 这将直接掩盖有价值的漏失流量的变化点与整体变化趋势。针对这一问题, 本文提出借助现场数据与漏失发生后的录井参数对漏失发生后漏失流量的实时变化进行计算。

在正常钻进的前提下, 可以认为进出口流量之比C是定值, 井漏发生后现场工程师通过钻井液池液面变化来统计一段时间内的总漏失量Q_L。因此, 通过总漏失量Q_L和进出口流量的比值C即可获得每个时刻的钻井液漏失量, 即漏失流量V_L, 再绘制相应的散点图, 进而得出井漏过程每一时刻的漏失流量。

进出口流量比值C:

C= $\frac{Q_{O} + Q_{L}}{Q_{I}}$ (1)

式中:C为进出口流量比, 无量纲; Q_O为一段时间内出口流量的和, m³; Q_I为一段时间内入口流量的和, m³; Q_L为记录的钻井液总漏失量, m³。

某时刻的钻井液漏失流量V_L:

V_L=CV_I-V_O(2)

式中:V_L为某时刻的漏失流量, m³/s; V_I为入口流量, m³/s; V_O为出口流量, m³/s。

1.2 漏失压力计算

表示钻井液循环当量密度(Equivalent Circulating Density, 简称ECD)计算模型定义为钻井液的当量静态密度(ESD)与钻井液流动造成的环空压耗当量密度之和。漏失压力p_L和循环当量密度ECD的计算分别为:

p_L=ECD× g× H(3)

ECD=ρ (1-C_a)+ρ _sC_a+ $\frac{p_{a}}{0.00981 H}$ (4)

式中:ρ 为钻井液密度, g/cm³; ρ _s为岩屑密度, g/cm³; C_a为环空岩屑浓度, %; p_a为环空压耗, MPa; g为重力加速度; H为井深, m。

其中环空岩屑浓度计算式为:

C_a= $\frac{t}{3600 (v_{c} - v_{s}) (1 - {d_{0}}^{2} / d^{2})}$ (5)

式中:t为钻速, m/h; d₀为钻杆外径, cm; d为井眼内径, cm; v_c为钻井液环空返速, m/s; v_s为岩屑沉降速度, m/s。

当流态为紊流时, 井段环空压耗^[9]为:

p_a= $\frac{2.04 fρ {v_{c}}^{2} L}{d - d_{0}}$ (6)

式中:L为钻杆长度, m; f为摩阻系数, 无量纲。

在公式(6)中的参数除摩阻系数f以外均可通过现场设计资料获得, 而摩阻系数 f 采用 Dodge 和 Metzner 推导出的半经验公式^[10]来计算:

$\frac{1}{\sqrt[]{f}}$ = $\frac{4}{n^{0.75}}$ lg[N_Re(f)^(1-0^.⁵ⁿ⁾]- $\frac{0.395}{n^{1.2}}$ (7)

式中:N_Re为紊流的常规雷诺系数; n为流动参数, 由公式(8)确定。

n= $\frac{d [\lg (d_{0} p_{a} / 4 L)]}{d [\lg (8 V_{L} / d_{0})]}$ (8)

通过ECD和漏失井的水力学参数设计便可以求得单次漏失发生时的具体时间点的井底漏失压力数据。

1.3 裂缝导流能力计算

基于单次漏失的录井数据, 可以全面分析该裂缝在漏失压力变化下, 钻井液漏失能力的变化率, 即裂缝的导流能力。通过对裂缝导流能力的定量分析可以得出该条裂缝对漏失压力的敏感性, 并指导该井后续堵漏作业及同区块中相邻井的钻井液当量密度设计与工艺参数设计。选取时刻1和时刻2, 在计算时可以认为这一次井漏发生后截取的这一段时间内钻遇裂缝的地层孔隙压力p_o为不变的, 则该次井漏裂缝的导流能力可以通过漏失流量与漏失压力曲线的变化趋势来表示, 即裂缝导流能力K:

K= $\frac{V_{1} - V_{2}}{(p_{1} - p_{o}) - (p_{2} - p_{o})}$ = $\frac{V_{1} - V_{2}}{p_{1} - p_{2}}$ (9)

式中:V₁为时刻1的漏失流量, m³/s; V₂为时刻2的漏失流量, m³/s; p₁为时刻1的漏失压力, MPa; p₂为时刻2的漏失压力, MPa; p_o为地层孔隙压力, MPa。

将漏失裂缝的导流能力和漏失压力的关系进行构图, 得到了裂缝导流能力与漏失压力的平面曲线图, 再对该曲线进行微分便得到了该条裂缝在漏失压力变化下, 导流能力的变化。

2 致漏裂缝类型的识别

通过某井井漏时现场实时录井数据进行分析, 绘制漏失流量和漏失压力的数据平面散点图, 再对散点图拟合, 然后对拟合曲线进行微分得到裂缝导流能力-漏失压力曲线图。对裂缝导流能力-漏失压力曲线图拟合后得到裂缝导流能力和漏失压力的变化趋势图, 再通过裂缝导流能力的变化趋势图对钻遇裂缝的性质进行识别与分类。

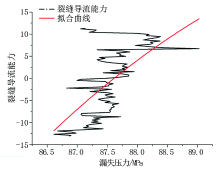
使用上述模型计算的某油田现场某井的两次井漏的裂缝导流能力-漏失压力曲线图见图1、图2。

	Figure Option View Download New Window
	图1 某井5 571 m漏失的导流能力-漏失压力曲线

	Figure Option View Download New Window
	图2 某井5 625 m漏失的导流能力-漏失压力曲线

(1)图1实例为某井5 571 m处发生的漏失。从图1可以看出, 随着漏失压力的下降, 裂缝的导流能力整体变化趋势为持续降低。当漏失压力大于87.6 MPa时裂缝导流能力为正数, 即随着漏失压力下降, 钻井液的漏失流量一直在增加。而当漏失压力小于87.6 MPa时裂缝导流能力变为负数, 即随漏失压力下降, 漏失流量也在持续下降。针对该裂缝, 其导流能力变化的临界点为漏失压力87.6 MPa, 并存在达到临界点前裂缝随着漏失压力下降漏失流量增加, 当低于临界点时裂缝又随漏失压力下降漏失流量显著下降的现象。可以认为发生这一现象的原因是当漏失压力小于临界点时, 裂缝的闭合开始成为影响裂缝漏失流量的主要因素, 从而导致漏失流量下降。我们把这一类型裂缝定义为诱导致漏裂缝。

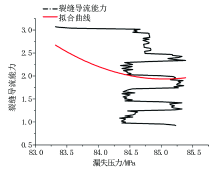
(2)图2实例为同一口井5 625 m处发生的漏失。在图2中, 随着漏失压力的下降, 裂缝的漏液能力变化不显著, 并且整个漏失过程中也不存在导流能力正负变化的临界点。可以认为漏失压力变化在整个漏失过程中对裂缝的漏失流量不产生主要影响, 因此这一类型裂缝可以被定义为自然致漏裂缝。

图1的拟合曲线为:

K=-0.96 ${p_{L}}^{2}$ +179.3p_L-8 331.17

图2的拟合曲线为:

K=0.25 ${p_{L}}^{2}$ -41.77p_L+1 778.05

3 实例校验

对某油田某区块7口井的51次井漏数据进行统计, 见表1。

表1 某油田现场7口井漏失裂缝性质判断

基于致漏裂缝类型识别方法对51次井漏进行区分, 其中31次为诱导致漏裂缝, 20次为自然致漏裂缝。在现场防漏堵漏作业中封堵的主要难题为诱导致漏裂缝。而诱导致漏裂缝的应力敏感性较好, 极易受到设置的工艺参数的影响, 因此需要对致漏类型进行区分。将诱导致漏裂缝类型区分出来之后, 再通过统计法计算该区块诱导致漏裂缝的漏失压差与漏失流量的关系曲线, 从而可以更好地指导现场防漏堵漏作业。

依照上文可以得到51组数据的全结果及31次诱导致漏结果, 将两个结果进行比对, 从而进行准确性验证。

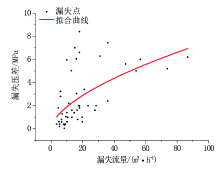
对7口井所有致漏裂缝的漏失数据(51次)进行拟合(图3), 拟合得出漏失方程为:

Δ p=0.479 33 ${V_{L}}^{0.5986}$ (10)

	Figure Option View Download New Window
	图3 某油田区块51次漏失压差与漏失流量的关系

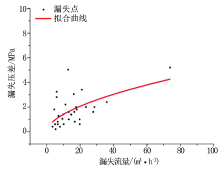
对裂缝进行分类后只对诱导致漏裂缝(31次)漏失数据进行拟合(图4), 得出漏失方程为:

Δ p=0.964 54 ${V_{L}}^{0.3412}$ (11)

	Figure Option View Download New Window
	图4 某油田区块31次漏失压差与漏失流量的关系

漏失压力为孔隙压力与漏失压差之和, 则潜山地层漏失压力为:

p_L=p_o+Δ p(12)

裂缝分类前后的漏失压力计算结果分别为:

p_L=p_o+0.479 33 ${V_{L}}^{0.5986}$ (13)

p_L=p_o+0.964 54 ${V_{L}}^{0.3412}$ (14)

选取数据样本中的一口井的一次漏失为例进行校验, 该井在5 820 m处发生了井漏。漏失发生时工况为钻进, 此时泵压为15.7 MPa, 泵冲为86冲, 钻井液密度为1.34 g/cm³, 漏失流量为54 m³/h。

结合现场资料由漏失方程公式(10)计算51次漏失得出的漏失压差为5.22 MPa, 而由漏失方程公式(11)计算31次一类漏失得到的漏失压差为3.76 MPa, 依据钻井工程设计方案, 该井5 420~7 556 m层段的地层孔隙压力当量密度为1.19~1.22 g/cm³。依据漏失压力方程公式(12), 计算出该层段的漏失压力为73.09~74.8 MPa(51次漏失)和71.63~73.34 MPa(31次漏失)。根据钻井工程设计的参数, 由公式(5)(6)(7)计算出环空压耗为5.15 MPa, 钻井液当量密度为1.39 g/cm³, 可以计算出漏失工况钻进时井底压力为74.13 MPa。

由51次漏失数据计算的漏失压力73.09 MPa< 74.13 MPa < 74.8 MPa, 即钻进时井底压力处于预测漏失压力的区间。而31次漏失数据计算的漏失压力71.63~73.34 MPa小于井底压力74.13 MPa, 说明钻进时井底压力大于预测漏失压力进而导致漏失。通过校核, 将裂缝类型识别并区分再进行漏失压力计算, 计算结果准确度更高、更符合现场的工程实际。

4 结论

(1)新型统计法分析诱导致漏裂缝的漏失压力和旧有的统计法相比具有更高的准确性。方法更符合工程实际, 能更好地指导今后的钻进工作及区块工艺参数和水力参数设计。

(2)在现场和钻井研究领域, 都缺乏结合现场实时钻进数据库进行的分析研究, 从而导致了部分理论研究脱离了工程实际, 不能很好地指导现场钻进工作。后续研究者可以尝试建立方法将二者紧密结合起来。

(编辑王丽娟)

参考文献

文献列表

[1]	DRUMMOND J M. An appraisal of fracture porosity[J]. Bulletin of Canadian Petroleum Geology, 1964, 12: 226-245. [本文引用:1]
[2]	POUISEN D K. A comprehensive theoretical treatment of fracturing fluid loss[R]. SPE 18 262, 1988. [本文引用:1]
[3]	MORITA N, BLACK A D, GUH G F. Theory of lost circulation pressure[R]. SPE 20 409, 1990. [本文引用:1]
[4]	DYKE C G, WU B, MILTON-TAYLER D. Advances in characterising natural fracture permeability from mud log data[J]. SPE Formation Evaluation, 1995, 10(3): 160-166. [本文引用:1]
[5]	LAVTOV A, TRONVOLL J. Modeling mud loss in fractured formation[R]. SPE88 700, 2004. [本文引用:1]
[6]	LAVTOV A, TRONVOLL J. Mud loss into a single fracture during drilling of petroleum wells: Modeling approach[C] ∥Proceedings of 6th International Conference on Analysis of Discontinuous Deformation. Trondheim, Norway: International Society for Rock Mechanics, 2003: 189-198. [本文引用:1]
[7]	金衍, 陈勉, 刘晓明, 等. 塔中奥陶系碳酸盐岩地层漏失压力统计分析[J]. 石油钻采工艺, 2007, 29(5): 82-84. JIN Yan, CHEN Mian, LIU Xiaoming, et al. Statistic analysis of leakage pressure of Ordovician carbonate formation in middle Tarim Basin[J]. Oil Drilling &Production Technology , 2007, 29(5): 82-84. [本文引用:1]
[8]	朱亮, 张春阳, 楼一珊, 等. 两种漏失压力计算模型的比较分析[J]. 天然气工业, 2008, 28(12): 60-61, 67. ZHU Liang, ZHANG Chunyang, LOU Yishan, et al. Comparative analysis between the mechanics based and statistics based calculation models for leakage pressure[J]. Natural Gas Industry, 2008, 28(12): 60-61, 67. [本文引用:1]
[9]	封卫强, 李琪, 孙腾飞. 钻井液循环当量密度影响因素分析[J]. 价值工程, 2012, 31(4): 22-23. FENG Weiqiang, LI Qi, SUN Tengfei. The ECD analysis of influencing factors[J]. Value Engineering, 2012, 31(4): 22-23. [本文引用:1]
[10]	DODGE D W, METZNER A B. Turbulent flow of non-newtonian systems[J]. Aiche Journal, 1959, 5(2): 189-204. [本文引用:1]

1964

0.0

... 1964年Drummond^[1]提出可利用天然裂缝性储集层的大量钻井液漏失资料来确定地层岩石孔隙度 ...

1988

0.0

... 1988年 Pouisen^[2]基于钻井流体漏失形态呈线性并平行于裂缝面、流体漏失服从达西定理、漏失流体是不可压缩的和储集层是无限平行于裂缝面4个假设前提推导出了描述水力裂缝中流体漏失的通用公式 ...

1990

0.0

... Morita^[3]提出了漏失压力理论, 分析了漏失压力影响因素 ...

1995

0.0

... 1992年 Dyke等^[4]详细论述了钻井过程中的钻井液漏失响应, 对钻井液漏失控制给出了合理的建议 ...

2004

0.0

... 2004年Alexandre Lavtov^[5]提出了裂缝性地层的漏失模型, 描述了钻井液在径向单裂缝中的漏失机理, 定量描述了钻井液实时漏失曲线 ...

2003

0.0

... 同年,Lavtov^[6]等提出假设钻井液为幂律流体,裂缝为有限长的平面圆盘状,裂缝宽度随压力线性变化,建立了单条裂缝的径向漏失模型 ...

2007

0.0

... 2007年金衍等^[7]通过现场漏失井深、工况、发生率、漏失通道进行统计分析,构建了统计法计算漏失压力的模型 ...

2008

0.0

朱亮, 张春阳, 楼一珊, 等. 两种漏失压力计算模型的比较分析[J]. 天然气工业, 2008, 28(12): 60-61, 67.

ZHU

Liang

, ZHANG

Chunyang

, LOU

Yishan

, et al. Comparative analysis between the mechanics based and statistics based calculation models for leakage pressure[J]. Natural Gas Industry, 2008, 28(12): 60-61, 67.

Drilling fluid leakage is affected by many factors during drilling, which makes it more difficult to determine the value of leakage pressure. Based on analysis of two main causes leading to drilling fluid leakage, the mechanicsbased and statisticsbased calculation models for leakage pressure were set up respectively. A calculation example has been performed by these two models .The result shows that the calculation results which deduced from statisticsbased calculation model was more tally with the actual situation than the mechanicsbased calculation model and can give a precise description of the high relevancy between leakage pressure and pressure difference, thus can be widely used in fields.

1.Hubei Province Key Laboratory for Petroleum Engineering, Yangtze University; 2.Petroleum Engineering College, Yangtze University; 3.Development & Production Department, CNOOC Ltd.; 4.Energy Technology & Services-Supervision & Technology Co., CNOOC Oil Base Group

钻井液发生漏失是多因素共同作用下的复杂问题，如何采用合适的计算模型来确定漏失压力的值一直以来都是一个难题。为解决此问题，在分析两种漏失种类的基础上，分别建立了漏失压力的力学模型和基于统计的漏失压力计算模型，并就两种模型的计算结果进行了实例计算分析，认为漏失压力的大小与压差有比较明显的关联性，压差越大，漏失速率越大。利用基于统计的漏失压力计算模型比漏失压力的力学模型得到的结果好，与现场实测数据相符合，具有较强的实用性。

... 2008年朱亮等^[8]将统计法建立的漏失压力计算模型与力学计算模型进行了比较,证明统计法要优于力学计算法 ...

2012

0.0

... 当流态为紊流时,井段环空压耗^[9]为: ...

1959

0.0

... 在公式(6)中的参数除摩阻系数f以外均可通过现场设计资料获得,而摩阻系数 f 采用 Dodge 和 Metzner 推导出的半经验公式^[10]来计算: ...