大港油田位于天津市与河北省境内, 其歧口凹陷探明的天然气资源量相当丰富, 主要分布在板桥、大张坨、千米桥等地区, 以板桥地区为主, 其他地区主要为零星分布的小规模气藏或出气点。天然气探明储量属沙河街组最高, 但其埋藏较深, 地震主频较低、分辨率差, 且目前气层钻遇率不高, 预测难度较大。近年来, 前人基于不同的时频分析方法在含气性检测方面做了大量的研究^{[1, 2, 3]}, 主要使用的方法是短时窗傅立叶变换、Cohen类的Wigner-Ville分布以及小波变换等时频分析方法^{[4, 5, 6]}; Castagna等^[7]阐述小波变换和匹配追踪两种分频技术指示油气的方法; 才巨宏等^[8]应用S变换时频技术预测孔洞缝储集层; 王飞等^[9]利用Hilbert-Huang变换联合平滑伪Wigner-Ville时频分布揭示信号在时间分布和频率分布上的差异进行流体性质识别; 李丛等^[10]应用平滑Wigner-Ville谱分解技术, 结合含气地层“ 高频能量衰减、低频能量增强” 的特点预测油气分布。尽管Wigner-Ville时频分布不受窗函数和窗函数长度选择的影响, 且时频局域性最好, 分辨率高, 但存在交叉项干扰, 限制了其应用^{[11, 12, 13]}。本文将模糊函数应用于Wigner-Ville时频分布, 在模糊函数域加Choi-Williams核函数, 可以有效地抑制交叉项, 较好地保持Wigner-Ville时频分布原有的时频局域性和分辨率, 将其应用于大港油田板桥地区沙河街组的含气性检测, 具有一定的效果。

Wigner-Ville时频分布是一种最基本的非线性表示^[14]。这种分布最初是由Wigner在量子力学研究中提出的, 信号x(t)的Wigner-Ville分布表示为:

W_x(t, ω )=∫ -∞∞x(t+ τ2)x^* (t- τ2)e^{-jω τ} dτ (1)

其中x^* 为x的共轭, 表达式(1)可以看作是某种能量分布特征函数的Fourier变换。式中t为时间变量, ω 为频率变量, τ 为时间滞后量(时延)。

当信号为x和y两复谐波信号叠加时, Wigner-Ville时频分布表达式为:

W_x+y(t, ω )=W_x (t, ω )+W_y (t, ω )+W_{x, y} (t, ω )+W_{y, x} (t, ω )(2)

其中:

W_{x, y}(t, ω )=∫ -∞∞x(t+ τ2)y^* (t- τ2)e^{-jω τ} dτ (3)

W_{y, x}(t, ω )=∫ -∞∞y(t+ τ2)x^* (t- τ2)e^{-jω τ} dτ (4)

式(3)与式(4)互为Wigner-Ville时频分布, 其中W_{x, y}(t, ω )=W^* _{y, x}(t, ω ), W_{x, y} (t, ω )+W_{y, x} (t, ω )为实数, 表达式(2)可以改写成表达式(5)。

W_x+y(t, ω )=W_x (t, ω )+W_y(t, ω )+2Re[W_{x, y}(t, ω )](5)

表达式(5)说明, 两信号和的Wigner-Ville时频分布不是它们各自的Wigner-Ville时频分布的和, 除了两个自项外, 还包含一个互项, 即交叉项。W_x(t, ω )和W_y(t, ω )称为信号项, 2Re[W_{x, y}(t, ω )]为交叉项。推广到具N个信号成分的Wigner-Ville时频分布, 也有类似的结论。

图1给出50 Hz和150 Hz两调制高斯叠加信号及其Wigner-Ville时频分布, 从信号的Wigner-Ville时频分布可以看出, 叠加信号中50 Hz和150 Hz两调制高斯信号在时频剖面上位于正确的位置, 而交叉项在这两信号之间。

图1

	Figure Option ViewDownloadNew Window
	图1 两个调制高斯信号的Wigner-Ville分布

在非平稳信号处理中, 模糊函数可以定义为:对瞬时相关函数作关于时间t的Fourier反变换, 而不是Fourier变换, 即:

A_x(τ , ν )= Ft→ν-1[R_x (t, τ )] =∫ -∞∞x(t+ τ2)x^* (t- τ2)e^{jν τ} dt(6)

式中ν 为频偏。

模糊函数式(6)和Wigner-Ville分布表达式(1)都是信号的双线性变换或瞬时相关函数R_x(t, τ )的某种线性变换。Wigner-Ville变换到时频域, 表示能量分布, 为能量域; 而模糊函数则变换到时延-频偏域, 表示相关, 为相关域。由式(1)和式(6)容易证明:

W_x (t, ω )= 12π∫ -∞∞∫ -∞∞A_x (τ , ν )e^{-j(ν t+ω τ )}dν dτ (7)

可见Wigner-Ville分布与模糊函数的Fourier二维变换等价, 只是相差一个常数因子1/2π 。

本文采用在模糊函数域加Choi-Williams核函数Φ (τ , ν )=exp[-α (τ ν )²]窗, 再进行Fourier二维变换到Wigner-Ville分布方式进行交叉项抑制^{[15, 16]}。

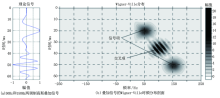
图2为50 Hz和150 Hz两调制高斯叠加信号在模糊函数域分布对其加Choi-Williams核函数窗抑制交叉项, 进而求取Wigner-Ville时频分布。图2a为叠加信号在模糊函数域内分布图, 各频率信号分量都以原点(0, 0)为中心混合在一起, 从这个意义上说, 模糊函数对各频率信号是模糊的, 而交叉项远离原点。图2b为Choi-Williams核函数窗, 其在原点(0, 0)的权系数为1, 向外逐渐趋于0。图2c为在模糊函数域加核函数窗抑制交叉项后的Wigner-Ville时频分布剖面。与图1b对比可以看出, 加核Wigner-Ville时频分布有效抑制了交叉项, 且能保持原有的时频局域性和分辨率。

图2

	Figure Option ViewDownloadNew Window
	图2 叠加信号在模糊函数域分布及核函数窗和加核Wigner-Ville时频分布

地震记录可以看作地震子波与反射系数褶积的结果, 用不同主频的雷克子波合成的信号更能检验不同时频分析方法在实际地震资料中的分辨能力。图3为由不同主频子波合成地震信号。在50 ms附近为一个40 Hz子波, 350 ms附近是10 Hz和40 Hz子波同向叠加, 500 ms附近是两个30 Hz子波时间上错位同向叠加, 650 ms附近是两个30 Hz和两个20 Hz子波时间上错位同向叠加, 900 ms附近是三个30 Hz子波时间上错位叠加其中一个反向叠加, 具体叠加方式如图3。图3a~图3d为不同时频分析方法对应的时频剖面图, 从图中可以看出, 核函数窗Wigner-Ville分布在650 ms附近能识别两个层、900 ms附近能识别三个层, 其分辨能力明显优于其他方法, 具有较高的时间和频率分辨率。

图3

	Figure Option ViewDownloadNew Window
	图3 不同主频子波叠加信号模型及其对应不同时频分析方法的时频剖面图

歧口凹陷板桥地区的天然气藏或出气点主要位于沙河街组, 平均埋深约4 700 m。由于气藏埋藏较深, 钻穿井少, 且目前对深层的烃源岩质量及规模认识不足, 资源潜力尚不落实, 这给深层气的预测带来很大困难。图4为B 1井录井测试成果图对应合成记录标定及井旁地震道加核Wigner-Ville时频分析剖面。图4a为B 1井录井测试成果图, 图中③和④处试油解释为水层, ②处试油解释为油层, ①处试油解释为气层, 产气约20 000 m³/d, 为本文研究的目标层。图4b为B 1井合成记录标定, 图中红色的合成记录叠合在地震剖面之上, 目标层位于沙河街组Es3²油组内。图4c为B 1井井旁地震道加核Wigner-Ville时频分析剖面, 总体来看沙河街组地震波峰值频率较低约为15 Hz, 从上往下地震峰值频率有明显向低漂移的趋势, 气层峰值频率明显降低且频带变窄。

图4

	Figure Option ViewDownloadNew Window
	图4 B 1井录井测试成果图对应合成记录标定及井旁地震道加核Wigner-Ville时频分布剖面

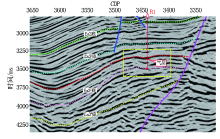
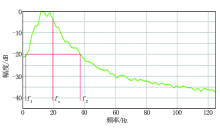
现将加核Wigner-Ville时频分布方法用于过B 1井地震剖面, 验证该方法的可行性。图5为研究区过B 1井地震剖面, 图中红色框标明B 1井的产气层并进行了解释, 红线表示气层顶界。图6为目的层附近的频谱(与图5中黄色矩形区域对应的频谱), 中心频率f_c为20 Hz, 峰值频率幅值衰减至20 dB时, 低频端频率f₁为3 Hz, 高端频率f₂为37 Hz。对该剖面进行加核Wigner-Ville时频分布方法计算, 并提取单一频率剖面, 寻找气层预测的优势频率。图7为采用加核Wigner-Ville时频分布方法计算后提取的10 、15、20、25 Hz的频率剖面。对比这4幅图可以看出, 在10 Hz的频率剖面中, 在B 1井的产气层出现相对的强能量团, 而浅层能量相对弱。随着频率增高, 单频剖面图中产气层强能量团逐渐减弱, 而浅层能量增强, 表明高频能量被气层吸收, 含气层的主频向低频移动, 出现了低频异常现象。

图5

	Figure Option ViewDownloadNew Window
	图5 过B1井地震剖面

图6

	Figure Option ViewDownloadNew Window
	图6 目的层附近的频谱图

图7

	Figure Option ViewDownloadNew Window
	图7 采用加核Wigner-Ville时频分布方法提取的不同单一频率的频率剖面

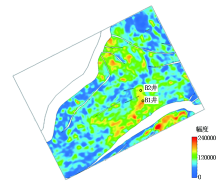
通过上述各个单频体分析, 10 Hz的单一频率体可以作为板桥区块Es3²油组含气性预测的优势频率, 沿图7a中红线(气层)开时窗提取振幅属性作为含气性预测图(图8)。

图8

	Figure Option ViewDownloadNew Window
	图8 板桥区块Es32含气性预测图

图8为沿层在10 Hz单频体上提取的均方根振幅属性图, 图中暖色调表示低频强能量含气有利区。综合地质认识和含气性预测, 在B 1井东北方向部署了B 2井兼探Es3²气层, B 2井试油解释为气层, 产气约16 800 m³/d。

(1)基于Wigner-Ville的时频分析方法, 因交叉项存在严重干扰了时间域、频率域的分辨率, 但通过在模糊函数域加Choi-Williams核函数窗, 较好地抑制了交叉项, 且保持了Wigner-Ville时频分析原有的时间分辨率、频率分辨率和聚能性。

(2)时频分析方法可提供时间域与频率域的联合分部的信息, 从已钻井可以清楚地掌握地震信号时频变化规律与含气性之间的关系, 可以选择一个含气性预测的优势频率, 进行储集层含气性预测。

(3)在大港油田板桥地区的应用表明, 该技术为储集层含气性预测提供了较好的指导作用, 值得进一步探索和研究。

(编辑 王丽娟)