岩屑XRF数据拟合随钻伽马方法研究

引用本文

刘有武. 岩屑XRF数据拟合随钻伽马方法研究[J]. 录井工程, 2020,31(4): 50-53.
LIU Youwu. Study on cuttings XRF data fitting with LWD gamma method[J]. Mud Logging Engineering, 2020,31(4): 50-53.
Doi:10.3969/j.issn.1672-9803.2020.04.008 复制到剪切板

Permissions

《录井工程》杂志社所有

岩屑XRF数据拟合随钻伽马方法研究

刘有武

中国石油长城钻探工程有限公司录井公司

作者简介: 刘有武工程师,1986年生,2008年毕业于重庆科技学院石油与天然气地质勘查专业,现在中国石油长城钻探录井公司地质检测中心从事岩石化学综合分析与解释工作。通信地址:124010 辽宁省盘锦市兴隆台区石油大街77号。电话:(0427)7852964。E-mail:359389794@qq.com

收稿日期: 2020-11-30

摘要

随着国内外旋转导向钻井技术的兴起,随钻伽马成为钻井过程中层位卡取及岩性识别的重要参照数据,同时也是跟踪、对比、调整井眼轨迹的主要依据。但目前国内外随钻仪器普遍存在仪器前端盲区较长的缺点,且部分井由于井下情况复杂不适合下随钻伽马测量设备,因此亟需一种通过岩屑来拟合伽马的方法填补此空缺。在采用数理统计方法筛选出岩石中与电测伽马相关性较好的6种特征元素的基础上,通过线性回归方程方法求取各特征元素的权重系数,最终得出拟合伽马数据。通过研究井及邻井验证,该方法拟合得出的随钻伽马与电测伽马曲线吻合度达到95%以上,完全能满足现场应用。

关键词: 相关系数; 线性回归方程; 拟合随钻伽马; 岩屑XRF分析

中图分类号:TE132.1 文献标志码:A

Study on cuttings XRF data fitting with LWD gamma method

LIU Youwu

GWDC Mud Logging Company, CNPC, Panjin, Liaoning 124010,China

Abstract

With the rise of rotary steering drilling technology at home and abroad, LWD gamma becomes an important reference data for horizon determination and lithology identification in drilling process, and also the main basis for tracking, comparing and adjusting well trajectory. But at present, there is a long blind area in the front of LWD instruments at home and abroad, and some wells are not suitable for running LWD gamma measuring equipment due to the complex downhole conditions. Therefore, a method to fit gamma by cuttings is urgently needed to fill this gap. On the basis of selecting six characteristic elements in rock with good correlation with electrical logging gamma by mathematical statistics method, the weight coefficient of each characteristic element was calculated by linear regression equation, and finally the fitting gamma data was obtained. Through the verification of research wells and offset wells, the coincidence degree of LWD gamma curve and electrical logging gamma curve obtained by this method is more than 95%, which can fully meet the field application.

Keyword: correlation coefficient; linear regression equation; fit LWD gamma; cuttings XRF analysis

文章图片

0 引言

伽马值是岩石的自然放射性指标, 它由岩石中放射性同位素的种类和含量决定。根据前人研究总结, 沉积岩的放射性一般有以下变化规律:一是随泥质含量的增加而增加; 二是随有机质含量的增加而增加; 三是随着钾盐和某些放射性矿物的增加而增加^[1]。由此可见, 岩石的放射性与岩石所含矿物种类及含量密切相关。矿物是单个元素或若干个元素在一定地质条件下形成的具有特定物理性质的化合物, 是构成岩石的基本单元^[2]。同一地质时期物源相同的情况下, 沉积岩的矿物组成基本相同, 可以根据数理统计原理分析岩屑XRF数据, 从而找出与岩石放射性相关性较好的元素, 再通过线性回归方程求得各元素的权重系数。

1 研究方法

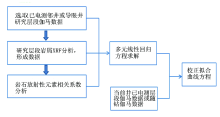
首先选取有电测伽马的邻井或导眼井中目的层段伽马数据, 与岩屑XRF数据进行多元线性回归方程求解, 然后再通过当前井已电测段或已有随钻伽马段进行拟合伽马公式系数修正, 最终得出本井拟合伽马模型。研究思路如图1所示。

	Figure Option View Download New Window
	图1 岩屑XRF数据拟合伽马模型

(1)XRF数据获取。现场取样及分析严格执行Q/SY 1862-2016《元素录井技术规范》。

(2)相关系数分析。岩石放射性元素相关性分析按Pearson相关系数的计算方法进行。分别将每一种元素的数值当成自变量, 与电测伽马进行相关性分析。公式如下^[3]:

r= $\frac{\sum (x_{i} - \overset{̅}{x}) (y_{i} - \overset{̅}{y})}{\sqrt[]{\sum (x_{i} {- \overset{̅}{x})}^{2} \sum (y_{i} {- \overset{̅}{y})}^{2}}}$

式中:r为两个变量的相关系数, r绝对值范围为0~1, 其绝对值越大说明相关性越好; x_i为某一井深一种元素的数值; y_i为对应井深的电测伽马值; $\overset{̅}{x}$ 为分析井段的元素平均值; $\overset{̅}{y}$ 为对应井段的电测伽马平均值。

(3)多元线性回归方程求解。可采用行列式按行(列)展开法则把高阶行列式降阶为低阶行列式计算, 或通过矩阵求解^[4]。

2 应用实例展示

研究选取A井6 220~6 549 m井段电测伽马数据及岩屑XRF数据进行研究展示, 选取Na、Mg、Al、Si、P、S、Cl、K、Ca、Ti、V、Cr、Mn、Fe、Co、Ni、Cu、Zn、As、Rb、Sr、Y、Zr、Nb、Mo、Ag、Cd、In、Sn、W、Pb、Th、U、Ba共34种元素数据分别与电测伽马数据进行相关性分析(表1), 然后取其中放射性相关系数居前6的元素即Fe、Co、Ni、Zn、Rb、W来求取多元线性回归方程。确定好放射性特征元素后按电测伽马值大小分别选取6个井深点的XRF元素数据(表2)。

表1 A井6 220~6 549 m井段放射性元素与电测伽马相关系数

表2 电测伽马对应放射性特征元素选点数据

利用EXCEL自带的MINVERSE逆矩阵函数公式及两个数组矩阵乘积公式MMULT解方程组得出六阶行列式求解数据表(表3)。

表3 六阶行列式求解数据

各变量对应方程组的解即为各放射性特征元素的权重系数, 因此可以得出六元线性方程如下:

c=18.337 799Fe+1.744 694Co-0.451 109Ni-2.433 629Zn+0.220 100Rb+40.878 567W+b

式中:c代表方程计算结果; Fe元素含量单位为%, Co、Ni、Zn、Rb、W元素含量单位为10^-6; b为方程式计算结果最小值为负值时的绝对值。

即c_min=18.337 799Fe+1.744 694Co-0.451 109Ni-2.433 629Zn+0.220 100Rb+40.878 567W

计算结果最小值为负值时, b=|c_min|, 如果c_min≥ 0则b=0。

在实际应用中要让拟合伽马与电测伽马曲线值的范围尽量接近, 需要乘以平均系数k= $\overset{̅}{G}$ / $\overset{̅}{c}$ 对拟合伽马进行调整(式中 $\overset{̅}{G}$ 为电测伽马平均值, $\overset{̅}{c}$ 为方程计算结果的平均值)。因此拟合伽马(g, 无量纲)最终方程式为:

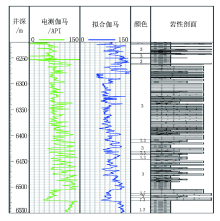
g=(18.337 799Fe+1.744 694Co-0.451 109Ni-2.433 629Zn+0.220 100Rb+40.878 567W+|c_min|) $\frac{\overset{̅}{G}}{\overset{̅}{c}}$ =(18.337 799Fe+1.744 694Co-0.451109Ni-2.433 629Zn+0.220 100Rb+40.878 567W+b)k

计算后得出A井拟合伽马公式中b=38.87, k=0.760 39。根据该拟合伽马公式计算出A井6 220~6 549 m井段拟合伽马数据(表4), 并绘制电测伽马与拟合伽马对比图(图2)。

表4 A井6 220~6 549m井段拟合伽马数据(部分)

	Figure Option View Download New Window
	图2 A井6 220~6 549 m井段电测伽马与拟合伽马曲线

由表4及图2可以看出, 通过XRF放射性相关特征元素数据拟合出的伽马数据及曲线, 与电测伽马数据及曲线吻合度较高, 曲线形态基本一致, 证明能够满足现场实际应用需求。

3 注意事项

该研究方法使用时需要注意以下几方面:

(1)提前做好电测资料收集工作, 必须有1口电测伽马数据邻井或部分已测随钻伽马数据。

(2)研究前必须进行岩电差深度校正工作, 确保电测数据与分析的岩屑XRF数据对应。

(3)同一区块不同层位沉积环境不同物源不同, 岩石矿物组成往往不同, 从而导致放射性特征元素不完全相同, 因此最好按层位分段分析放射性特征元素并建立线性回归方程模型, 这样准确度会更高。

(4)同一区块同一层位不同井应用同一拟合伽马模型时, 拟合伽马公式中系数b及k应分别进行校正。

4 结论

通过相关系数公式筛选出与放射性相关性较好的特征元素, 采用矩阵解多元线性回归方程的方法可以得出岩屑XRF数据拟合伽马模型。利用该模型计算得出的拟合伽马数据与电测伽马数据较接近, 形成的对比曲线重合度较高, 完全能够满足现场通过岩屑拟合伽马数据的需求。

岩屑XRF数据拟合随钻伽马技术应用前景广阔, 主要体现在以下几个方面:

(1)通过岩屑拟合伽马可以对电测伽马起到相互验证的作用, 为层位卡取及岩性识别提供参考依据。

(2)特殊情况下可替代电测伽马, 如复杂工程原因导致电测失败或不能下随钻伽马测量设备的情况下, 可以使用该方法替代电测伽马。

(3)可以拟合出电测仪器前端盲区及电测口袋伽马数据。

(4)在水平井中可以减少由于随钻伽马无信号或电池续航能力不足导致的起下钻次数, 节省钻井成本。

(5)水平井中可以预测近钻头伽马数据, 有助于及时调整井眼轨迹保证优质储集层钻遇率。

需要说明的是, 该方法在现场应用中受客观条件影响, 有一定的局限性:一是测量密度只能按岩屑录取间距进行; 二是当前PDC钻头新钻井工艺条件下岩屑普遍细碎, 从混样中挑选新鲜真岩屑难度较大, 如果真岩屑挑选不准会对XRF数据准确度有一定影响; 三是该方法目前在沉积岩中通过验证证明应用效果较好, 火成岩及变质岩地层中的应用效果还需进一步验证。

(编辑姜萍)

参考文献

文献列表

[1]	刘向君, 刘堂晏, 刘诗琼. 测井原理及工程应用[M]. 北京: 石油工业出版社, 2006. LIU Xiangjun, LIU Tangyan, LIU Shiqiong. Logging principle and engineering application[M]. Beijing: Petroleum Industry Press, 2006. [本文引用:1]
[2]	刘向君, 熊健, 梁利喜. 岩石物理学基础[M]. 北京: 石油工业出版社, 2018. LIU Xiangjun, XIONG Jian, LIANG Lixi. Fundamentals of petrophysics[M]. Beijing: Petroleum Industry Press, 2018. [本文引用:1]
[3]	盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2010. SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability theory and mathematical statistics[M]. Beijing: Higher Education Press, 2010. [本文引用:1]
[4]	陈殿友, 术洪亮. 线性代数[M]. 北京: 清华大学出版社, 2007. CHEN Dianyou, SHU Hongliang. Linear algebra[M]. Beijing: Tsinghua University Press, 2007. [本文引用:1]