钻时和扭矩变换方法在岩性变化判断中的应用探讨

引用本文

薛硕, 吴昊晟, 倪朋勃, 荆文明, 邴磊. 钻时和扭矩变换方法在岩性变化判断中的应用探讨[J]. 录井工程, 2021,32(2): 26-30.
XUE Shuo, WU Haosheng, NI Pengbo, JING Wenming, BING Lei. Discussion on application of drilling time and torque conversion method in lithology change identification[J]. Mud Logging Engineering, 2021,32(2): 26-30.
Doi:10.3969/j.issn.1672-9803.2021.02.005 复制到剪切板

Permissions

《录井工程》杂志社所有

钻时和扭矩变换方法在岩性变化判断中的应用探讨

薛硕, 吴昊晟, 倪朋勃, 荆文明, 邴磊

中法渤海地质服务有限公司

作者简介：薛硕助理工程师,1990年生,2015年本科毕业于长江大学石油工程专业,现在中法渤海地质服务有限公司从事录井工作。通信地址:300450 天津市经济技术开发区信环西路19号天河科技园1号楼3层。电话:17702284060。E-mail:xueshuo@cfbgc.com

收稿日期: 2021-05-06

摘要

钻时是反映地层岩性变化的重要依据,但随着钻井技术和钻井工艺的不断改进,钻时变化愈加不明显,不能直接反映岩性的变化,而扭矩受工况和工艺影响较大,往往只作为判断砂岩的辅助手段。渤海油田以盆地构造为主,地质及油藏条件复杂,为了提高钻时和扭矩的可比性,分别基于 dc指数公式和摩擦力公式提出了新的钻时变换和扭矩变换摩擦系数方法,并将二者结合起来用于判断岩性的变化。选取渤中区块的BZ-X-2井作为例证进行探讨,结果表明:同实际钻时和实际扭矩相比,变换后的钻时和摩擦系数具有明显的可比性,判断砂泥岩变化及储集层厚度的准确率更高,提高了录井剖面的符合率。

关键词: 钻时; 扭矩; dc指数; 综合录井; 岩性划分

中图分类号:TE132.1 文献标志码:A

Discussion on application of drilling time and torque conversion method in lithology change identification

XUE Shuo, WU Haosheng, NI Pengbo, JING Wenming, BING Lei

ChinaFrance Bohai Geoservices Co.,Ltd.,Tianjin 300450,China

Abstract

Drilling time is important in reflecting changes in stratum lithology. However,with the improvement of drilling technology and craft,drilling time changes are becoming obscure and cannot directly reflect changes in lithology. Affected by working conditions and craft,torque is often only used as an auxiliary means to identification sandstone. Bohai Oilfield is mainly basin structure with complex geological and reservoir conditions. To improve the comparability of drilling time and torque,new drilling time conversion and torque conversion friction coefficient methods are proposed based on dc index formula and friction formula respectively,and are combined to identification changes in lithology. The BZ-X-2 well in Bozhong Block is selected as an example for discussion. Results signify that converted drilling time and friction coefficient are of obvious comparability compared with actual drilling time and torque,and higher accuracy in identification of sand shale changes and reservoir thickness,thereby improving the coincidence rate of mud logging profile.

Keyword: drilling time; torque; dc index; compound logging; lithology identification

文章图片

0 引言

自动送钻技术已在渤海油田广泛应用, 自动送钻是通过控制系统自动调节钻压, 让钻机按钻井工艺要求, 达到一个理想的、稳定的机械钻速^[1]。机械钻速的定义是单位纯钻进时间内所钻的进尺^[2], 而钻时是钻进单位地层所需要的时间^[3], 两者互为倒数关系, 故机械钻速一旦稳定, 钻时也就稳定了, 然而稳定的钻时不利于岩性的归位。

所以说自动送钻技术在提高钻井效率的同时, 也给录井判断岩性的变化带来了难度。为此, 亟需寻求一种钻时和扭矩的变换方法, 使钻时和扭矩的变化规律更接近地层岩性的变化规律。本文通过分析非地层因素对钻时和扭矩的影响, 以dc指数公式和摩擦力公式为变换的理论依据, 拟合出适合当前钻井技术的钻时变换公式及扭矩变换摩擦系数公式。

1 钻时及扭矩的影响因素

我们应用的钻时, 必须是在相同的情况下取得^[4]。但在实际钻井过程中, 这种“ 相同的情况” 是不存在的, 扭矩亦是如此。只有分析钻时和扭矩的影响因素, 并将这些影响因素量化, 才能消除其对钻时和扭矩的影响, 从而真实地反映出地层所蕴含的信息。

1.1 钻时的影响因素

影响钻时的主要因素有:

(1)岩性:岩性是地层固有的特性, 只有将钻压、钻井液性能、钻头类型、钻头转速、钻头直径等非地层因素定量化, 钻时才能更好地反映地层固有的特性。当其他因素不变时, 岩性疏松、硬度小, 则钻时低, 反之则钻时高。

(2)钻压:当其他因素不变时, 钻压大, 则钻时低, 反之则钻时高。

(3)钻头类型:当其他因素不变时, PDC钻头比牙轮钻头钻进速度快, 钻时低(有例外情况)^[4]。

(4)钻井液性能:当其他因素不变时, 当量钻井液循环密度大, 则钻时增加; 反之, 则钻时减小。

(5)钻头转速:当其他因素不变时, 钻头转速快, 钻时低, 反之则钻时高。

(6)钻头直径:当其他因素不变时, 钻头直径小, 则钻时低, 反之钻时高。

1.2 钻具扭矩的影响因素

影响钻具扭矩变化的主要因素包括来自钻头与井底摩擦所产生的扭矩和钻柱与井壁摩擦所产生的扭矩。钻井过程中, 钻井液性能呈阶段性变化, 也就是说在某个阶段内钻井液的摩擦力扭矩是一定的, 它对扭矩变化的影响微乎其微, 所以不是影响钻具扭矩变化的主要因素。

1.2.1 钻柱与井壁的摩擦力扭矩

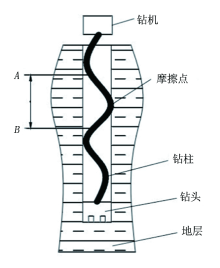
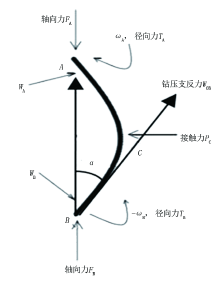
旋转钻进时, 在综合力的作用下, 旋转的钻柱与井壁摩擦, 钻柱发生正弦弯曲或螺旋弯曲^[5]。如图1所示。对图1中, 微段AB进行受力分析, 如图2所示。

	Figure Option View Download New Window
	图1 钻柱与井壁摩擦示意

	Figure Option View Download New Window
	图2 钻柱微段运动受力分析

钻压与钻压支反力是一对轴向相互作用力, 它们大小相等, 方向相反。根据力的正交分解及正弦定理, 可得接触力P_C表达式:

P_C=Wsinα (1)

式中:P_C为接触力, N; W为钻压, N; α 为钻柱微段的弯曲角度, (° )。

根据力矩定义及公式(1), 可得微段AB与井壁的摩擦力扭矩表达式:

T_f=μ _pWsinα × $\frac{1}{2}$ D_P(2)

式中:T_f为微段AB摩擦力扭矩, N· m; D_P为钻柱直径, m; μ _p为钻柱与井壁的摩擦系数, 无量纲。

钻柱摩擦力扭矩M_f是由若干个微段AB摩擦力扭矩T_f 组成, 即:

M_f=∑ T_f (3)

式中:M_f为钻柱摩擦力扭矩, N· m。

1.2.2 钻头与井底的摩擦力扭矩

佩西尔(Pessier)在1992年通过钻头岩石简易模型, 推导出钻头摩擦力扭矩公式^[6]:

M_B=∫ $\overset{\frac{d_{b}}{2}}{\underset{0}{}}$ ∫ $\overset{2 π}{\underset{0}{}}$ ρ ² $\frac{4 μ_{b} W}{π {d_{b}}^{2}}$ dρ dθ = $\frac{μ_{b} W d_{b}}{3}$ (4)

式中: M_B为钻头摩擦力扭矩, N· m ; d_b为钻头直径, m; μ _b为钻头与岩石间的摩擦系数, 无量纲。

1.2.3 钻头摩擦力扭矩与钻柱摩擦力扭矩的比较

比较公式(2)与公式(4), 由于钻柱在井壁中的弯曲角度α 非常微小, 可得:

M_B> > T_f(5)

由公式(3)可知, 钻柱摩擦力扭矩是由若干个微段AB摩擦力扭矩组成的; 由公式(5)可知, 钻头摩擦力扭矩远远大于微段AB摩擦力扭矩。比较公式(3)和公式(5)可以发现, 当井深较浅或直井情况下, 微段AB较少, 钻头摩擦力扭矩远远大于钻柱摩擦力扭矩, 这时可以借助钻头摩擦力扭矩判断井底岩性。当井深较深时, 越来越多的微段AB叠加进来, 使得钻柱摩擦力扭矩逐渐增加, 对钻头摩擦力扭矩的干扰越来越大。鉴于钻柱在井壁里的运动情况十分复杂且每个接触点的摩擦系数不一样, 在实际工作中很难准确计算井壁摩擦力扭矩, 因此在浅井或直井情况下, 可以借助钻头摩擦力扭矩判断井底岩性, 钻具扭矩表达式可近似为钻头摩擦力扭矩表达式:

M≈ M_B= $\frac{μ_{b} W d_{b}}{3}$ (6)

式中:M为钻具扭矩, N· m 。

2 钻时变换公式

雷姆(Rehm)和迈克林顿(McClendon)考虑到钻井液密度变化会对钻速产生影响, 于1971年提出校正的d指数, 即dc指数公式。目前, 国内常用dc指数经验公式为^{[7, 8, 9]}:

dc= $\frac{\lg [3.282 / (nt)]}{\lg (0.0684 W / d_{b})}$ × $\frac{ρ_{w}}{ρ_{ce}}$ (7)

式中: dc为dc指数, 无量纲; n为转盘转速, r/min; t为钻时, min/m; W为钻压, kN; d_b为钻头直径, mm; ρ _w为地层水密度, g/cm³; ρ _ce为循环当量钻井液密度, g/cm³。

由公式(7)可以得到dc指数和其他参数之间的函数关系, 将公式(7)变换形式得到公式(8), 即关于钻时t的函数方程:

t=10^x(8)

其中:x=lg( $\frac{3.282}{n}$ ) $- dc \times \lg {(\frac{0.0684 W}{d_{b}})}^{\times \frac{ρ_{ce}}{ρ_{w}}}$

dc指数是一个综合考虑了多种钻井因素影响的无量纲参数, 常用来描述地层的“ 可钻性” “ 坚硬性” “ 密实性” ^[9], 而钻时则是一个受多种非地层因素影响较大的参数。由公式(8)可见, 钻时与dc指数存在一定函数关系。将公式(8)中的转盘转速、钻压、循环当量钻井液密度定量化处理, 钻时便具有与dc指数相同的特性, 而且钻时的变化区间比dc指数大, 具有更强的可比性。

3 扭矩变换摩擦系数公式

本文在第1.2.3节中提到, 在浅井或直井情况下, 钻具扭矩表达式可近似为钻头摩擦力扭矩表达式。由公式(6)可知, 影响钻头摩擦力扭矩的主要因素是钻压、摩擦系数、钻头直径, 而摩擦系数是钻头与岩石之间的固有特性, 是本文所要利用的, 所以将公式(6)变形为公式(9), 即扭矩变换摩擦系数表达式为:

μ _b≈ $\frac{3 M}{W d_{b}}$ (9)

如公式(9)所示, 摩擦系数可以看作是钻头与岩石之间固有特性的表征, 对钻头直径和钻压进行定量化处理, 便可以利用摩擦系数来判断岩性的变化。

4 计算方法及判断原则

计算方法:钻时变换公式(8)和扭矩变换摩擦系数公式(9)都含有钻头直径这个因数, 所以在运用变换公式时, 要按照不同的钻头直径(每一开钻井程序)分段计算。

判断原则:当变换钻时相对变低且变换摩擦系数相对变高时, 可能进入砂岩层; 当变换钻时相对变高且变换摩擦系数相对变低时, 可能进入泥岩层。由于钻时只代表地层的可钻性, 不能完全代表地层岩性, 还要根据岩屑和气体参数综合考虑。扭矩变换得到摩擦系数可以反映地层岩性的变化, 但可能会受工程因素的影响, 所以要将变换钻时和变换摩擦系数两者结合起来综合考虑, 才能提高判断的准确性。

5 变换钻时和变换摩擦系数应用效果

5.1 应用实例

笔者利用钻时变换结合扭矩变换摩擦系数的方法在对渤海油田数十口井进行的实验表明, 该方法具有一定的实用性。现以渤中区块BZ-X-2井为例予以说明。该井是一口定向井, 井斜最大达到24.98° , 位于渤海海域渤南低凸起中段南部区域。由于该井2 150~2 235 m井段(斜深)井深、井斜较大, 实际钻时和实际扭矩变化不明显, 岩性归位难度大, 本文选取该井段作为研究对象。

BZ-X-2井从500 m开始录井到2 277 m结束, 该期间一直使用直径为241 mm 的PDC钻头, 平均转盘转速为157.76 r/min, 平均循环当量钻井液密度(ECD)为1.15 g/cm³, 平均钻压为2.34 t(22.91 kN), 地层水密度为1.03 g/cm³, 将以上数据代入钻时变换公式(8)则得到:

${t=10}^{\lg (\frac{3.282}{157.76}) - dc \times \lg (\frac{0.0684 \times 22.91}{241}) \times \frac{1.15}{1.03}}$ (10)

同理将钻头直径0.241 m代入扭矩变换摩擦系数公式(9)则得到:

μ _b≈ $\frac{3 M}{0.241 W}$ (11)

将表1中的dc指数代入公式(10)便可计算出变换钻时, 将表1中的扭矩和钻压代入公式(11)便可计算摩擦系数。

表1 BZ-X-2 井2 150~2 200 m井段(斜深)钻井参数(部分数据)

5.2 结果验证

BZ-X-2井2 150~2 235 m井段(斜深)属于馆陶组地层, 该段地层的自然电位曲线和自然伽马曲线在砂岩段特征明显(图3), 因此利用自然电位曲线和自然伽马曲线作为砂、泥岩地层的划分依据。图3中, 1号和3号砂岩层, 自然电位和自然伽马曲线呈砂岩趋势, 但实际钻时和实际扭矩未发生明显变化, 而变换钻时和变换摩擦系数却发生了明显的变化, 说明变换后的钻时和摩擦系数能够明显地反映地层信息。

	Figure Option View Download New Window
	图3 BZ-X-2井测井、录井曲线对比

1号、2号、3号砂岩层均具有变换钻时变低和变换摩擦系数变高的规律, 因此变换钻时和变换摩擦系数结合起来判断, 能有效提高卡取砂岩层的准确性。而且变换钻时和变换摩擦系数的变化界面明显, 利于岩性的划分和油气层厚度的确定。

6 结论

本文选择dc指数公式和摩擦力公式所蕴含的函数关系作为依据, 提出一种钻时变换和扭矩变换摩擦系数相结合的判断方法。为了体现这种判断方法的实用性, 选取渤海油田数十口井进行试验, 并以BZ-X-2井作为例证。理论和实践表明, 本文的变换方法有效, 对录井工作质量的提高是有所帮助的。该方法具有以下优势:

(1)岩性变化时, 变换钻时和变换摩擦系数有明显的变化, 有更强的可比性, 能捕捉到实际钻时和实际扭矩捕捉不到的地质信息。

(2)通过变换钻时和变换摩擦系数相结合的判断方法, 能切实提高岩性归位的准确性。

(3)变换钻时和变换摩擦系数的变化界面明显, 利于岩性的划分和油气层厚度的确定。

(4)变换钻时和变换摩擦系数的变化规律更符合地层岩性的变化规律, 钻时变换和扭矩变换摩擦系数方法在当今先进的钻井工艺条件下具有一定的实用性。

在应用钻时变换和扭矩变换摩擦系数方法时, 必须保证录取的钻井参数的准确性, 准确的参数是决定变换成败的关键。

(编辑李特)

参考文献

文献列表

[1]	房昕. “地壳一号”万米钻机自动送钻模拟研究[D]. 长春: 吉林大学, 2014. FANG Xin. Simulation study on automatic bit feeding of Diqiao One the 10000-meter drilling rig[D]. Changchun: Jilin University, 2014. [本文引用:1]
[2]	汤凤林. 岩心钻探学[M]. 武汉: 中国地质大学出版社, 2009. TANG Fenglin. Core drilling[M]. Wuhan: China University of Geosciences Press, 2009. [本文引用:1]
[3]	王守君, 刘振江, 谭忠健, 等. 中海油勘探监督手册·地质分册[M]. 北京: 石油工业出版社, 2013. WANG Shoujun, LIU Zhenjiang, TAN Zhongjian, et al. Geology volume of CNOOC exploration supervision hand book[M]. Beijing: Petroleum Industry Press, 2013. [本文引用:1]
[4]	刘宜平. 浅谈钻时在录井及钻井中的应用[J]. 江汉石油职工大学学报, 2004, 17(2): 32-33. LIU Yiping. Application of drilling time in mud logging and well drilling[J]. Journal of Jianghan Petroleum University of Staff and Workers, 2004, 17(2): 32-33. [本文引用:2]
[5]	高鹏举. 地质钻探中钻柱与孔壁间摩擦扭矩实验研究[D]. 北京: 中国地质大学(北京), 2013. GAO Pengju. Frictional torque between string and borehole wall in geological drilling[D]. Beijing: China University of Geosciences(Beijing), 2013. [本文引用:1]
[6]	PESSIER R C, FEAR M J. Quantifying common drilling problems with mechanical specific energy and a bit-specific coefficient of sliding friction[C]∥SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 1992. [本文引用:1]
[7]	陈永明. 压差校正可提高D指数地层压力检测精度[J]. 钻采工艺, 1994, 17(4): 25-28. CHEN Yongming. Differential pressure correction improving the accuracy of D index formation pressure detection[J]. Drilling & Production Technology, 1994, 17(4): 25-28. [本文引用:1]
[8]	冯蓓华, 阿太忠, 侯民香. 浅谈 dc指数在随钻分析中的应用[J]. 青海石油, 2010(1): 110-116. FENG Beihua, E Taizhong, HOU Minxiang. Application of dc index in analysis while drilling[J]. Qinghai Petroleum, 2010(1): 110-116. [本文引用:1]
[9]	李普涛. 基于 dc指数公式的钻时变换方法探讨[J]. 录井工程, 2014, 25(1): 16-20. LI Putao. Discussion on drilling time conversion method based on dc index formula[J]. Mud Logging Engineering, 2014, 25(1): 16-20. [本文引用:2]

2014

0.0

... 0 引言自动送钻技术已在渤海油田广泛应用,自动送钻是通过控制系统自动调节钻压,让钻机按钻井工艺要求,达到一个理想的、稳定的机械钻速^[1] ...

2009

0.0

... 机械钻速的定义是单位纯钻进时间内所钻的进尺^[2],而钻时是钻进单位地层所需要的时间^[3],两者互为倒数关系,故机械钻速一旦稳定,钻时也就稳定了,然而稳定的钻时不利于岩性的归位 ...

2013

0.0

2004

0.0

... 1 钻时及扭矩的影响因素我们应用的钻时,必须是在相同的情况下取得^[4] ...

... (3)钻头类型:当其他因素不变时,PDC钻头比牙轮钻头钻进速度快,钻时低(有例外情况)^[4] ...

0.0

... 旋转钻进时,在综合力的作用下,旋转的钻柱与井壁摩擦,钻柱发生正弦弯曲或螺旋弯曲^[5] ...

1992

0.0

... 佩西尔(Pessier)在1992年通过钻头岩石简易模型,推导出钻头摩擦力扭矩公式^[6]: ...

1994

0.0

... 目前,国内常用dc指数经验公式为^[7,8,9]: ...

0.0

... 目前,国内常用dc指数经验公式为^[7,8,9]: ...

2014

0.0

... 目前,国内常用dc指数经验公式为^[7,8,9]: ...

... ^[9],而钻时则是一个受多种非地层因素影响较大的参数 ...