复合油藏流动系数场分布规律研究

引用本文

姚君波, 袁立, 章威, 陈晓祺, 龙明. 复合油藏流动系数场分布规律研究[J]. 录井工程, 2021,32(4): 138-142.
YAO Junbo, YUAN Li, ZHANG Wei, CHEN Xiaoqi, LONG Ming. Study on the distribution law of flow coefficient field in composite reservoir[J]. Mud Logging Engineering, 2021,32(4): 138-142.
Doi:10.3969/j.issn.1672-9803.2021.04.025 复制到剪切板

Permissions

《录井工程》杂志社所有

复合油藏流动系数场分布规律研究

姚君波, 袁立, 章威, 陈晓祺, 龙明

中海石油(中国)有限公司天津分公司

作者简介：姚君波工程师,1986年生,2014年毕业于成都理工大学油气田开发专业,现在中海石油(中国)有限公司天津分公司渤海石油研究院主要从事油气田开发研究工作。通信地址:300459 天津市滨海新区海川路2121号渤海石油大厦B座。电话:15022080302。E-mail:yaojb4@cnooc.com.cn

收稿日期: 2021-11-05

基金: 国家科技重大专项“渤海油田高效开发示范工程”(编号:2016ZX05058); 中海石油(中国)有限公司科技攻关项目“渤海双高油田挖潜关键技术研究”(编号:YXKY-2018-TJ-04)

摘要

目前研究流动系数场非均质性主要是试井分析,但获取的地层参数只是波及范围内的一个平均值,无法提供储层的流动系数场非均质性精确分布状况。通过对径向复合及多层复合油藏进行分析,得出压力响应动态特征与油藏流动系数场分布规律之间的内在联系,压力导数曲线形态的异常上翘和下掉能够反映流动系数场的分布,说明利用压力测试数据分析地层流动系数的变化规律是可行的,最终利用单井压力测试资料识别井筒附近油藏流动系数场分布规律。在渤海油田BH 1-9井实施注聚合物开发后,油藏流动场分布规律需要重新认识,利用该研究方法可以直观得出准确的聚合物推进后的反演成果,说明此反演预测方法对油田合理高效开发具有指导意义。

关键词: 流动系数场; 试井分析; 复合油藏; 压力响应特征; 分布规律

中图分类号:TE132.1 文献标志码:A

Study on the distribution law of flow coefficient field in composite reservoir

YAO Junbo, YUAN Li, ZHANG Wei, CHEN Xiaoqi, LONG Ming

CNOOC (China) Tianjin Branch, Tianjin 300459, China

Abstract

At present, the study of flow coefficient field heterogeneity is mainly well test analysis, but the formation parameters obtained are only an average value within the sweep range, which cannot provide accurate distribution of reservoir flow coefficient field heterogeneity. The inherent relationship between the dynamic characteristics of pressure response and the distribution law of reservoir flow coefficient field is got by analyzing the radial composite and multi-layer composite reservoirs. The abnormal upwarping and downwarping of pressure derivative curve pattern can reflect the distribution of flow coefficient field, indicating that it is feasible to analyze the variation law of formation flow coefficient by using pressure test data. Finally, the distribution law of reservoir flow coefficient field near wellbore is identified by single well pressure test data. After the implementation of polymer injection development in BH1-9 well of Bohai Oilfield, the distribution law of reservoir flow field needs to be re-recognized. The research method can intuitively obtain the inversion results after accurate polymer propulsion, which shows that this inversion prediction method has guiding significance for rational and efficient oilfield development.

Keyword: flow coefficient field; well test analysis; composite reservoir; pressure response characteristic; distribution law

文章图片

0 引言

油藏流动系数场的非均质情况十分复杂, 严重制约着油藏的开发水平。利用试井资料及其他动态资料求取流动系数场真实分布状况, 是国内外石油工业界的一个热点和难点问题。

杨志刚等^[1]通过建立封闭边界条件下多层复合油藏模型利用Stehfest数值反演得出Laplace空间解, 绘制无因次压力及压力导数与无因次时间双对数理论图板, 并详细分析多种情形下井底压力动态响应五个阶段的影响因素, 对油田多层复合油藏的开发具有一定的指导意义。王俊超等^[2]建立了引入有效井径的复合油藏球向渗流模型, 利用 Laplace 变换将渗流模型转化为 Laplace空间的常微分方程边值问题, 在此基础上李笑萍等^[3]的研究考虑了井筒储集效应和表皮效应, 并采用反褶积方法计算了井筒储集效应。但是以上研究对复杂复合油藏研究较少。本次研究利用流动系数非均质油藏渗流数学模型, 获得地层流动系数分布与压力恢复双对数曲线中压力导数值之间的理论联系, 结合前人的研究成果^{[1, 2, 3]}, 建立单井附近地层流动系数场分布预测数学模型, 识别井筒附近油藏流动系数场分布规律。

1 复合油藏井底压力动态响应特征

1.1 径向复合油藏井底压力动态响应特征

径向复合油藏物理模型围绕井轴的两个圆形复合区域, 尽管每一区域内流动系数变化不大, 可视为均质各向同性, 但两个圆形区域间的流动系数差异大。

根据渗流力学基本原理, 利用微元法的思想, 结合状态方程、连续性方程、达西渗流方程, 建立径向复合油藏无因次数学模型^[2], 进一步利用Laplace数学变换的基本原理, 对无因次化数学模型进行拉氏变换, 得到径向复合油藏拉氏空间渗流数学模型, 内、外区渗流微分方程满足Laplace方程的通解表达式如下:

${\bar{p}}_{iD}$ =A₁I₀ (r_D $\sqrt[]{u}$ )+A₂K₀(r_D $\sqrt[]{u}$ )(1)

${\bar{p}}_{oD}$ =A₃I₀ (r_D $\sqrt[]{η_{io} u}$ )+A₄K₀ (r_D $\sqrt[]{η_{io} u}$ )(2)

式中: ${\bar{p}}_{iD}$ 为无因次原始地层压力; ${\bar{p}}_{oD}$ 为无因次储层压力; r_D为无因次半径; u为Laplace变量; η 为扩散系数比; I₀(x)、K₀(x)为虚综量零阶Bessel函数; A₁、A₂、A₃、A₄为方程待定系数。

由内外边界条件和界面连接条件求解A₁、A₂、A₃、A₄的表达式, 则Laplace空间无因次井底压力计算公式^[4]为:

${\bar{p}}_{wfD}$ =A₁[I₀( $\sqrt[]{u}$ )-S $\sqrt[]{u}$ I₁( $\sqrt[]{u}$ )]+A₂[K₀( $\sqrt[]{u}$ )

+S $\sqrt[]{u}$ K₁ ( $\sqrt[]{u}$ )](3)

其中:A₁= $\frac{α_{10}}{α_{11}}$ - $\frac{α_{12}}{α_{11}} \frac{β_{20} β_{12} - β_{22} β_{10}}{β_{12} β_{21} - β_{22} β_{11}}$

A₂= $\frac{β_{20} β_{12} - β_{22} β_{10}}{β_{12} β_{21} - β_{22} β_{11}}$

A₃= $\frac{β_{10} β_{21} - β_{11} β_{20}}{β_{12} β_{21} - β_{22} β_{11}}$

A₄=- $\frac{α_{43}}{α_{44}} \frac{β_{10} β_{21} - β_{11} β_{20}}{β_{12} β_{21} - β_{22} β_{11}}$

α ₁₀=1; β ₁₀=- $\frac{α_{21} α_{10}}{α_{11}}$ ; β ₁₁=α ₂₂- $\frac{α_{21} α_{12}}{α_{11}}$ ; β ₁₂=α ₂₃- $\frac{α_{24} α_{43}}{α_{44}}$ ; β ₂₀=- $\frac{α_{31} α_{10}}{α_{11}}$ ; β ₂₁=α ₃₂- $\frac{α_{31} α_{12}}{α_{11}}$ ; β ₂₂=α ₃₃- $\frac{α_{34} α_{43}}{α_{44}}$

α ₁₁=C_Du²I₀( $\sqrt[]{u}$ )-u $\sqrt[]{u}$ (C_DuS+1)I₁( $\sqrt[]{u}$ )

α ₂₁=I₀(R_iD $\sqrt[]{u}$ )

α ₁₂=C_Du²K₀( $\sqrt[]{u}$ )+u $\sqrt[]{u}$ (C_DuS+1)K₁( $\sqrt[]{u}$ )

α ₂₂=K₀(R_iD $\sqrt[]{u}$ )

α ₂₄=-K₀(R_iD $\sqrt[]{η_{12} u}$ )

α ₃₁=M_io $\sqrt[]{u}$ I₁(R_iD $\sqrt[]{u}$ )

α ₃₂=-M_io $\sqrt[]{u}$ K₁(R_iD $\sqrt[]{u}$ )

α ₃₄= $\sqrt[]{η_{io} u}$ K₁(R_iD $\sqrt[]{η_{io} u}$ )

α ₂₃=α ₃₃=α ₄₃=α ₄₄=0

式中: ${\bar{p}}_{wfD}$ 为拉氏空间无因次井底压力; S为表皮系数; C_D为井筒系数; α 、β 为Laplace待定系数; R_iD为无因次外区外边界半径, m; M_io为储层流度比; I₁(x)、K₁(x)为虚综量一阶Bessel函数。

通过公式(3)得出径向复合油藏井底无因次压力响应拉氏解, 利用Stehfest数值反演原理^[3]获得相应的实空间解, 并分析其压力动态特征及影响因素。

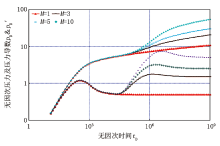
流度比是指驱替液流度与被驱替液(原油)流度的比值。流度比的大小直接影响着驱替液的波及体积, 进而影响采收率。从图1流度比M_io对复合油藏直井井底压力动态影响的关系图可以得出:流度比M_io对压力和压力导数双对数曲线的影响主要表现在压力波从内区到外区的过渡流动阶段以及后期的总径向流动阶段。若M_io> 1, 说明内区流动系数好于外区流动系数, 系统径向流动阶段的压力导数曲线位于内区上方; 若M_io< 1, 说明内区流动系数比外区差, 系统径向流动阶段的压力导数曲线位于内区的下方。流度比差异越大, 过渡阶段的压力导数曲线越陡, 过渡阶段持续的时间就越长。总径向流动阶段压力导数双对数曲线位置取决于流度比的大小, 其值为M_io/2。因此, 从流度比影响因素可以看出, 压力导数曲线的异常波动实际上反映了地层流动系数参数的变换规律。

	Figure Option View Download New Window
	图1 流度比对井底压力动态的影响

1.2 多层复合油藏井底压力动态响应特征

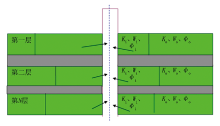
依据地层中流体为单相、弱可压缩液体、满足平面径向渗流和等温渗流之间不存在窜流的多层复合油藏渗流物理模型如图2所示。油藏在纵向上发育多套油层, 且受沉积等地质因素影响, 每一油层在平面上都呈现出径向复合的特点。

	Figure Option View Download New Window
	图2 多层复合油藏渗流物理模型

依据前面物理模型假设, 利用渗流力学基本原理, 建立多层复合油藏化渗流无因次数学模型^{[5, 6, 7, 8, 9]}:利用Laplace变换的基本性质, 将多层复合油藏渗流无因次数学模型进行拉氏变换, 则获得其相应的拉氏表达式, 根据Laplace方程通解形式, 内、外区井底压力响应的通解为:

${\bar{p}}_{j iD}$ =A_j₁I₀(r_D $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )+A_j₂K₀(r_D $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )(4)

${\bar{p}}_{j oD}$ =A_j₃I₀(r_D $\sqrt[]{η_{j io} u}$ )+A_j₄K₀ (r_D $\sqrt[]{η_{j io} u}$ )(5)

式中: ${\bar{p}}_{j iD}$ 为内区井底无因次压力响应值; ${\bar{p}}_{j oD}$ 为外区井底无因次压力响应值; ω 为储容比; k为串流系数; j为层数(j=1, 2, …, n)。

将通解形式代入外边界条件和界面连接条件, 可以获得A_j₁、A_j₂、A_j₃、A_j₄的具体表达式, 代入内边界条件和外边界条件, 则多层复合油藏井底压力响应数学模型为^[6]:

${\bar{p}}_{wD}$ = $\frac{1}{u (C_{D} u - F)}$ (6)

式中: ${\bar{p}}_{wD}$ 为多层复合油藏井底无因次压力响应值; F为压力响应综合系数。

F= $\overset{n}{\sum_{j = 1}}$ k_j[E_j $\frac{1}{a_{3} E_{j} + b_{3}} \sqrt[]{\frac{ω_{j}}{k_{j}} u}$ I₁( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )-

$\frac{1}{a_{3} E_{j} + b_{3}} \sqrt[]{\frac{ω_{j}}{k_{j}} u}$ K₁( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )]

E_j= $\frac{b_{2} c_{1} - b_{1} c_{2}}{a_{1} c_{2} - a_{2} c_{1}}$

a₁=I₀(R_j_fD $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

a₂=k₀(R_j_fD $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

a₃=I₀( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )-S_j $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ I₁( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

b₁=k₀(R_j_fD $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

b₂=- $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ k₁(R_j_fD $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

b₃=k₀( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )+S_j $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ k₁( $\sqrt[]{\frac{ω_{j}}{k_{j}} u}$ )

c₁=k₀(R_j_iD $\sqrt[]{η_{j io} u}$ )

c₂=- $\frac{\sqrt[]{η_{j io} u}}{M_{j io}}$ k₁(R_j_iD $\sqrt[]{η_{j io} u}$ )

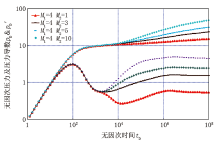
其中, R_j_fD为第j层无因次内区内边界半径; R_j_iD为第j层无因次外区外边界半径。从图3流度比对多层复合油藏井底压力动态响应特征的影响图中可以得出:主力层的流度比变化对曲线的影响较大, 第二径向流动段主要受主力层外区物性控制, 流度比越大, 第二径向流动段的台阶就相对越高。此外, 如果第二层的物性相等, 压力导数曲线出现一个明显的凹槽, 监测到层间窜流的流动阶段。

	Figure Option View Download New Window
	图3 主力层流度比对多层复合油藏井底压力动态的影响

2 单井压力测试资料预测流动系数场分布

本次研究利用ISA反演算法^[3]进行研究, 该方法基于扰动理论, 假设压力波所反映的瞬时平均流动系数值是探测区域内某个环形空间的流动系数场的体积加权平均, 这个环形区域的内径为r_i=0.12 $\sqrt[]{t_{D}}$ , 外径为r_o=2.34 $\sqrt[]{t_{D}}$ , 利用实测压力数据确定流动系数分布场步骤如下 ^{[10, 11, 12, 13, 14]}:

(1)利用实际压力测试数据, 根据瞬时平均流动系数 $\frac{kh}{μ}$ = $\frac{9.71 \times 10^{- 4} qb}{Δ p'_{w}}$ , 计算任意时刻瞬时流动系数 $\frac{{\hat{K}}_{n} h}{μ}$ 的大小;

(2)由探测半径与传播时间的关系式r_n=2 $\sqrt[]{\frac{3.6 k_{n} t_{n}}{ϕμ C_{t}}}$ , 计算不同时间对应的油藏探测半径 r_n;

(3)由无因次时间 ${\hat{t}}_{D}$ = $\frac{3.6 \hat{k} t}{ϕ C_{t} μ {r_{w}}^{2}}$ 的表达式, 计算出相应的无因次拟时间, 为流动系数场修正作准备;

(4)由流动系数场修正公式δ ( $\frac{μ}{Kh}$ )_n= $\frac{{(\frac{μ}{Kh})}_{n} - {(\frac{μ}{Kh})}_{n - 1} + N (t_{n})}{D (t_{n})}$ , 计算压降时的流动系数场修正量δ ( $\frac{μ}{Kh}$ )_n, 式中:

$\mathrm{N}\left(t_{n}\right)=

\sum_{i=2}^{n-1} \delta\left(\frac{\mu}{K h}\right)_{n-1} \int_{Z_{0 \mathrm{D}}}^{Z_{i-1 \mathrm{D}}} \sqrt{\pi} \hat{Z}_{\mathrm{D}} \exp \left(-\frac{\hat{Z}_{\mathrm{D}}^{2}}{2}\right) W_{1 / 2, 1 / 2}\left(\hat{Z}_{\mathrm{D}}^{2}\right) \mathrm{d} \hat{Z}_{\mathrm{D}}$ (7)

$\mathrm{D}\left(t_{n}\right)=1-\int_{Z_{0 \mathrm{D}}}^{Z_{i-1 \mathrm{D}}} \sqrt{\pi} \hat{Z}_{\mathrm{D}} \exp \left(-\frac{\hat{Z}_{\mathrm{D}}^{2}}{2}\right) W_{1 / 2, 1 / 2}\left(\hat{Z}_{\mathrm{D}}^{2}\right) \mathrm{d} \hat{Z}_{\mathrm{D}}$(8)

(5)由实际流动系数场计算公式( $\frac{μ}{Kh}$ )_n= $\frac{1}{{(\frac{μ}{Kh})}_{n - 1} + δ {(\frac{μ}{Kh})}_{n}}$ , 计算出任意位置流动系数 $\frac{{\hat{K}}_{n} h}{μ}$ 的分布, 得到t_n时刻对应的探测半径r_n下的流动系数值 $\frac{{\hat{K}}_{n} h}{μ}$ , 从而获得油藏流动系数的真实分布。

上述公式中:μ 为流体粘度, mPa· s; ϕ 为孔隙度, %; C为压缩系数, 1/MPa; δ 为弹性储容比, 无量纲; h为油层厚度, m; q为产量, m³/d; t_D为无因次时间; K为渗透率, mD。

3 矿场应用

渤海油田主要含油层系为明化镇组下段Ⅱ 、Ⅲ 油组。储层特征表现为高孔渗特征, 岩石孔隙发育较好, 分布均匀, 连通性较好。明下段油藏类型主要为岩性-构造油藏, 饱和压力高, 地饱压差小, 弹性能量较弱。2018年BH 1-9井开始注聚合物开发, 从表1可以看出各地层参数的变化反映出随注水的深入地层性质逐步变化的过程。从图4可以看出2018年、2019年由于注聚影响曲线有所不同, 地层聚合物推进预测结果来看, 2018年聚合物段塞推进到距BH 1-9井40 m处, 2019年聚合物段塞在50 m处, 2020年聚合物段塞在70 m处。

表1 历年压降参数对比

	Figure Option View Download New Window
	图4 BH 1-9井聚合物带推进反演及反演成果

4 结论

本次研究从径向复合、多层复合油藏的压力动态特征可以得出, 通过压力导数数学模型得出的曲线形态所显示的异常上翘形态和异常下掉的形态在一定程度上反映了油藏井筒附近流动系数场的分布, 从渗流力学基本原理出发, 建立了考虑流动系数非均匀分布的油藏渗流数学模型, 获得了压力导数曲线与流动系数之间的内在联系, 最后建立了单井附近流动系数场ISA反演预测算法。通过矿场试验可以看出利用单井压力测试资料数据分析油藏中地层流动系数的变化规律是具有一定指导意义的。

编辑王丙寅

参考文献

文献列表

[1]	杨志刚, 陈玉祥, 王霞. 考虑外边界影响的多层复合油藏试井解释数学模型[J]. 石油化工应用, 2011, 30(3): 16-19. YANG Zhigang, CHEN Yuxiang, WANG Xia. Logging interpretation mathematical model of multi-bed composite reservoir considering the influence of boundary[J]. Petrochemical Industry Application, 2011, 30(3): 16-19. [本文引用:2]
[2]	王俊超, 李顺初, 许丽. 基于解的相似结构的复合油藏球向渗流模型[J]. 桂林理工大学学报, 2012, 32(4): 624-627. WANG Junchao, LI Shunchu, XU Li. Spherical fluids flow models in composite reservoir based on similar structure of solution wellbore radius[J]. Journal of Guilin University of Technology, 2012, 32(4): 624-627. [本文引用:3]
[3]	李笑萍, 张大为. 数理方法与试井数学模型[M]. 北京: 石油工业出版社, 1993. LI Xiaoping, ZHANG Dawei. Mathematical method and well test mathematical model[M]. Beijing: Petroleum Industry Press, 1993. [本文引用:4]
[4]	李顺初, 刘平礼, 赵立强. 复合油藏储层中压力分布的求解[J]. 西南石油学院学报, 2000, 22(4): 76-79. LI Shunchu, LIU Pingli, ZHAO Liqiang. Solution of composite reservoir pressure distribution model[J]. Journal of Southwest Petroleum Institute, 2000, 22(4): 76-79. [本文引用:1]
[5]	邓远忠, 陈钦雷, 刘尉宁. 复合油藏非自喷DST试井数学模型的建立及其解的特征[J]. 石油大学学报(自然科学版), 1998, 22(6): 56-60. DENG Yuanzhong, CHEN Qinlei, LIU Weining. Mathematical model for non-flowing drillstem tests (DST) in composite reservoir[J]. Journal of the University of Petroleum, China, 1998, 22(6): 56-60. [本文引用:1]
[6]	刘启国, 冯宇, 董凤玲. 受界面附加阻力影响的双重介质径向复合油藏试井解释模型研究[J]. 油气井测试, 2005, 14(3): 11-13. LIU Qiguo, FENG Yu, DONG Fengling. Study on testing interpretation model of dual medium and radial compound reservoir influenced by interface addition friction[J]. Well Testing, 2005, 14(3): 11-13. [本文引用:2]
[7]	陈方方, 贾永禄, 乔忠明, 等. 三重介质油藏渗流模型与试井样版曲线[J]. 新疆石油地质, 2008, 29(3): 350-353. CHEN Fangfang, JIA Yonglu, QIAO Zhongming, et al. Flow model and well test type curves for triple-medium reservoirs[J]. Xinjiang Petroleum Geology, 2008, 29(3): 350-353. [本文引用:1]
[8]	付春权, 尹洪军, 贾俊飞. 复合油藏垂直裂缝井压力动态分析[J]. 大庆石油学院学报, 2008, 32(2): 113-115. FU Chunquan, YIN Hongjun, JIA Junfei. Pressure behavior analysis of vertically fractured well in composite reservoir[J]. Journal of Daqing Petroleum Institute, 2008, 32(2): 113-115. [本文引用:1]
[9]	徐有杰, 刘启国, 王瑞, 等. 复合油藏压裂水平井复杂裂缝分布压力动态特征[J]. 岩性油气藏, 2019, 31(5): 161-168. XU Youjie, LIU Qiguo, WANG Rui, et al. Pressure transient of fractured horizontal well with complex fracure distribution in composite reservoir[J]. Lithologic Reservoirs , 2019, 31(5): 161-168. [本文引用:1]
[10]	王志愿, 徐建平, 汪芸, 等. 非均质油藏水平井试井分析技术研究及应用[J]. 油气井测试, 2014, 23(5): 20-22. WANG Zhiyuan, XU Jianping, WANG Yun, et al. Research and application of well test analysis technology for horizontal wells in heterogeneous reservoirs[J]. Well Testing, 2014, 23(5): 20-22. [本文引用:1]
[11]	邬伦, 刘瑜, 张晶, 等. 地理信息系统——原理、方法和应用[M]. 北京: 科学出版社, 2001: 180-183. WU Lun, LIU Yu, ZHANG Jing, et al. Principle, method and application of geographic information system[M]. Beijing: Science Press, 2001: 180-183. [本文引用:1]
[12]	王道富. 边界元方法在试井分析中的应用研究[D]. 成都: 西南石油学院, 2004. WANG Daofu. Application of boundary element method in well test analysis[D]. Chengdu: Southwest Petroleum Institute, 2004. [本文引用:1]
[13]	石国新, 聂仁仕, 路建国, 等. 2区复合油藏水平井试井模型与实例解释[J]. 西南石油大学学报(自然科学版), 2012, 34(5): 99-104. SHI Guoxin, NIE Renshi, LU Jianguo, et al. Well test model of horizontal well in 2-zoned composite reservoir and example interpretation[J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2012, 34(5): 99-104. [本文引用:1]
[14]	邓元洲, 宋军政, 李鸘, 等. 地层流动系数场动态监测技术研究及应用[J]. 钻采工艺, 2014, 37(4): 51-53. DENG Yuanzhou, SONG Junzheng, LI Shuang, et al. Research and application of dynamic monitoring technology for formation flow coefficient field[J]. Drilling & Production Technology, 2014, 37(4): 51-53. [本文引用:1]

2011

0.0

... 杨志刚等^[1]通过建立封闭边界条件下多层复合油藏模型利用Stehfest数值反演得出Laplace空间解,绘制无因次压力及压力导数与无因次时间双对数理论图板,并详细分析多种情形下井底压力动态响应五个阶段的影响因素,对油田多层复合油藏的开发具有一定的指导意义 ...

... 本次研究利用流动系数非均质油藏渗流数学模型,获得地层流动系数分布与压力恢复双对数曲线中压力导数值之间的理论联系,结合前人的研究成果^[1,2,3],建立单井附近地层流动系数场分布预测数学模型,识别井筒附近油藏流动系数场分布规律 ...

2012

0.0

... 王俊超等^[2]建立了引入有效井径的复合油藏球向渗流模型,利用 Laplace 变换将渗流模型转化为 Laplace空间的常微分方程边值问题,在此基础上李笑萍等^[3]的研究考虑了井筒储集效应和表皮效应,并采用反褶积方法计算了井筒储集效应 ...

... 根据渗流力学基本原理,利用微元法的思想,结合状态方程、连续性方程、达西渗流方程,建立径向复合油藏无因次数学模型^[2],进一步利用Laplace数学变换的基本原理,对无因次化数学模型进行拉氏变换,得到径向复合油藏拉氏空间渗流数学模型,内、外区渗流微分方程满足Laplace方程的通解表达式如下: ...

1993

0.0

... 通过公式(3)得出径向复合油藏井底无因次压力响应拉氏解,利用Stehfest数值反演原理^[3]获得相应的实空间解,并分析其压力动态特征及影响因素 ...

... 2 单井压力测试资料预测流动系数场分布本次研究利用ISA反演算法^[3]进行研究,该方法基于扰动理论,假设压力波所反映的瞬时平均流动系数值是探测区域内某个环形空间的流动系数场的体积加权平均,这个环形区域的内径为r_i=0 ...

2000

0.0

... 由内外边界条件和界面连接条件求解A₁、A₂、A₃、A₄的表达式,则Laplace空间无因次井底压力计算公式^[4]为: ...

1998

0.0

... 依据前面物理模型假设,利用渗流力学基本原理,建立多层复合油藏化渗流无因次数学模型^[5,6,7,8,9]:利用Laplace变换的基本性质,将多层复合油藏渗流无因次数学模型进行拉氏变换,则获得其相应的拉氏表达式,根据Laplace方程通解形式,内、外区井底压力响应的通解为: ...

2005

0.0

... 将通解形式代入外边界条件和界面连接条件,可以获得A_j₁、A_j₂、A_j₃、A_j₄的具体表达式,代入内边界条件和外边界条件,则多层复合油藏井底压力响应数学模型为^[6]: ...

2008

0.0

2008

0.0

2019

0.0

2014

0.0