引用本文
唐诚, 王崇敬, 梁波, 顾炎午, 李柯. 基于机器学习算法的页岩气评价参数计算模型研究[J]. 录井工程, 2021,32(4): 18-22.
TANG Cheng, WANG Chongjing, LIANG Bo, GU Yanwu, LI Ke. Study on shale gas evaluation parameter calculation model based on machine learning algorithm[J]. Mud Logging Engineering, 2021,32(4): 18-22.
Doi:10.3969/j.issn.1672-9803.2021.04.003  
Permissions
Copyright©2021, 《录井工程》杂志社
《录井工程》杂志社 所有
基于机器学习算法的页岩气评价参数计算模型研究
唐诚①, 王崇敬①, 梁波①, 顾炎午①, 李柯②
①中石化经纬有限公司西南录井分公司
②中石化西南油气分公司石油工程监督中心

作者简介：唐诚 高级工程师,1979年生,2000年毕业于重庆石油高等专科学校石油地质专业,现在中石化经纬有限公司西南录井分公司从事科研工作。通信地址:621000 四川省绵阳市科创园区园艺街13号。电话:18084888276。E-mail:xnljtangcheng@163.com

收稿日期: 2021-10-22
基金: 中石化石油工程技术股份服务公司项目“基于机器学习的页岩气录井解释参数模型研究”(编号:SG19-20Q)
摘要

由于大量页岩气水平井的测井项目少甚至不测井,导致甜点评价参数匮乏。通过优选机器学习算法,开展岩石密度、有机碳、岩石成分的计算模型训练,建立了利用元素录井数据计算页岩评价参数的计算模型。计算结果对比表明,支持向量机、多元自适应回归样条、神经网络三种算法的效果均较好,其中支持向量机算法的模型计算效果最佳。应用结果表明,基于机器学习算法形成的页岩评价参数计算模型与其他方法实测结果趋势吻合性好、误差小,能为页岩气井提供重要的评价参数。

关键词: 页岩气; 元素录井; 密度; 有机碳; 岩石组分; 机器学习; 支持向量机
中图分类号:TE132.1 文献标志码:A
Study on shale gas evaluation parameter calculation model based on machine learning algorithm
TANG Cheng①, WANG Chongjing①, LIANG Bo①, GU Yanwu①, LI Ke②
①Southwest Mud Logging Branch of Sinopec Matrix Corporation, Mianyang, Sichuan 621000,China
②Petroleum Engineering Supervision Center of Sinopec Southwest Oil-Gas Company, Deyang 618099,China
Abstract

Because a large number of shale gas horizontal wells have few or no logging services, resulting in the lack of sweet spot evaluation parameters. By optimizing the machine learning algorithm, carrying out the calculation model training of rock density, organic carbon and rock composition, a calculation model for calculating shale evaluation parameters using element logging data is established. The comparison of the calculation results shows that all the three algorithms of support vector machine, multivariate adaptive regression splines and neural network work well, among which support vector machine algorithm has the best model calculation effect. The application results prove that the shale evaluation parameter calculation model based on machine learning algorithm fits well with the measured results of other methods, with small error, and can provide important evaluation parameters for shale gas wells.

Keyword: shale gas; element logging; density; organic carbon; rock composition; machine learning; support vector machine
0 引言

四川盆地及周缘地区的海相页岩气勘探开发已取得重大突破[1, 2], 在页岩气解释评价方面也取得了重要成果。当前普遍认为含气页岩储层的典型响应特征具有高自然伽马、高有机碳、低岩石密度的特征, 并广泛应用密度、中子、伽马能谱、电阻率等测井项目来评价地层孔隙度、含气饱和度、有机碳含量、获取镜质体反射率Ro、计算矿物组分体积含量等[3, 4]。但是, 页岩气开发的降本增效压力大, 且普遍采用水平井施工, 由于水平井段长, 绝大部分水平井大幅度减少测井项目, 部分工区的开发井甚至取消了测井项目, 也不开展岩石热解录井, 仅依靠随钻伽马测井资料与气测录井资料开展储层评价等工作, 导致测试选层时缺乏可靠的评价依据。因此, 亟需依托录井数据开展页岩气评价参数的计算方法研究, 为页岩气井的储层评价、测试选层提供可靠的依据, 满足页岩气开发的需要。

1 研究现状

川南地区页岩气目的层为五峰组-龙马溪组一段, 自下而上细划分为①-⑨号层, 其中①-④号层具有高TOC、高脆性矿物、低黏土、低密度的特征, 为主要的开发层系, 为了确保开发效益, 主要采用水平井进行钻探[1]。

1.1 解释评价现状

由于页岩气储层的岩性、物性、含气性等特征与常规油气藏相比有明显的不同, 难以通过常规手段来描述、评价页岩气。勘探初期在常规测井的基础上, 大量开展了ECS、Litho Scanner特殊测井技术的应用, 并辅以岩心含气量测量、电镜扫描、全岩分析等分析化验手段, 形成了页岩气“ 六性” 关系评价方法, 岩石组分、总有机碳、岩石密度等均是重要的评价参数, 并在解释评价过程中广泛应用[1, 2, 3, 5, 6], 页岩气随钻评价方法则以录井评价为主。赵红燕等[7]应用钻时比值、烃对比系数、岩石热解等方法, 开展页岩储层地化特征和含气性综合评价。随着特殊录井技术的推广应用, 唐谢等[8]通过岩石热解、元素录井、气测与工程录井、岩屑自然伽马能谱录井建立了长宁地区的页岩录井随钻解释评价方法。顾炎午等[9]应用逐步回归方法, 基于元素数据开展了页岩气评价参数的随钻计算研究, 建立了岩石组分、岩石密度、孔隙度等参数的录井计算模型。这些研究为页岩气的解释评价技术发展起到了积极推动作用。

1.2 存在的主要问题

1.2.1 大量开发井压缩了测井项目甚至不测井

测井项目在页岩气解释评价过程中发挥了重要的作用, 特别是岩石密度测井是评价页岩气甜点的关键参数[5, 6]。但是页岩气开发井基本为水平井, 因长水平段条件下测井风险大, 相当部分的页岩气区块取消了放射性测井项目。同时由于页岩气开发的降本增效压力大, 大量的开发井已经完全取消了测井项目, 导致完井后没有测井资料可以采用, 缺少测井评价参数。

1.2.2 水平井工况限制了常规录井解释方法应用

页岩气水平井以油基钻井液为主, 气测背景值高, 为了防止井壁坍塌, 钻井液密度相对较高, 导致钻遇油气时气测显示变化并不明显, 故水平段基本不使用岩石热解录井, 岩屑伽马能谱录井在中石化区块内没有得到推广应用。由于钻时受钻井工况的影响较大, 使用旋转导向工具钻进时钻时很低, 而使用LWD工具滑动钻进时钻时普遍较高, 常规录井解释方法受到了极大的限制, 缺乏有效的录井解释评价参数。

1.2.3 现有方法的计算精度不能完全满足需求

唐谢、顾炎午等[8, 9]研究了利用录井数据计算页岩评价参数的计算模型, 取得了积极进展, 但采用的方法以单参数拟合、多参数线性回归为主。已发表的文献表明, 计算钙质、硅质含量的相关系数仅为0.57~0.71, 表明评价参数之间存在复杂的非线性关系, 常规的线性计算模型不能完全满足需求。

2 计算模型研究

基于元素数据开展岩石组分及评价参数的计算方法研究, 能为解释评价提供依据[9], 但目前计算的准确性还有提升的空间。机器学习算法能够从大量的数据中学习到相关的规律和逻辑, 利用学习获取的规律预测未知事物, 在工业界得到了广泛的应用[10], 因此有必要基于机器学习算法建立计算模型, 提高计算的准确性。由于岩石组分是脆性评价的关键, 而岩石密度、总有机碳是含气性评价的重点[5, 6, 11], 本文针对岩石组分、岩石密度、总有机碳三个参数研究计算模型。

2.1 建立模型的流程

机器学习算法众多, 算法性能高度依赖于调优参数(超参数)的选择, 因此调优参数的设定是重要的步骤。通常采用交叉验证(CV)来进行模型的训练, 把原始数据分组, 一部分为训练集, 另一部分为验证集, 首先用训练集对模型进行训练, 再利用验证集来测试训练得到的模型, 根据拟合度(r2)对模型进行评价, r2越接近1, 说明拟合度越好[10]。

计算模型的建立流程确定如下:根据拟合对象选择合适的录井数据, 构成训练数据集; 选择不同的机器学习算法对数据进行训练, 利用CV交叉验证的方法进行调优参数的优选, 根据拟合度(r2)从训练结果中优选出最佳模型。

2.2 算法优选与模型训练

机器学习是人工智能的核心, 是通过利用数据, 训练出模型, 然后使用模型预测的一种方法, 主要有监督学习、无监督学习和强化学习三种类型[12]。它们各有不同的适应范围, 在不同的机器学习类型里, 又有非常多的算法, 不同的算法对最终的分析结果有明显影响。因此, 需要针对不同的应用场景与应用目的, 开展算法分析与优选。

本次研究的重点是页岩气评价参数的计算或预测, 主要用到的是监督学习中的回归算法。线性回归与逻辑回归应用非常广泛, 模型易于理解, 实现简单, 但泛化能力弱, 对于非线性问题拟合较差; 决策树、随机森林算法在决策与分类方面效果显著, 但在应用于回归中时预测能力有限; 支持向量机、神经网络、多元自适应回归样条通常在应用于回归问题时, 其非线性映射能力较强, 具有良好的拟合及预测能力, 泛化能力较强[10, 12]。因此, 本文选择支持向量机、多元自适应回归样条、神经网络三种算法来开展页岩气评价参数模型的研究。

2.2.1 支持向量机算法

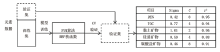
支持向量机(SVM)算法主要取决于核函数的选择, 径向基核函数(RBF)应用最广, 需要确定的参数少, 可以减少应用过程中的复杂程度。两项调优参数分别为RBF核函数参数的解析估计值Sigma和代价参数C。其中C表示对误差的宽容度, C值高容易过拟合, C值低容易欠拟合。Sigma会影响每个支持向量对应的RBF的作用范围:如果Sigma过大, 那么此时支持向量的辐射范围就非常小, 对于未知样本分类效果很差, 存在训练准确率可以很高, 而测试准确率不高的可能; 若Sigma 过小, 将使模型受限制太多, 被选定的支持向量的辐射范围很大, 则会造成平滑效应太大, 无法在训练集上得到特别高的准确率, 也会影响测试集的准确率, 从而影响泛化性能[10, 12]。模型训练流程及验证结果如图1所示。训练结果表明, 硅质矿物的效果最差, r2为0.88, DEN与黏土矿物效果最佳, r2均达到0.95。

图1 基于支持向量机算法的模型训练过程及调优参数的确定结果

2.2.2 多元自适应回归样条算法

多元自适应回归样条(MARS)能自适应处理高维数据。该方法的本质是将每一个预测变量(输入参数)设定一个切分点拆成两组, 然后在每一组中建立预测变量与结果变量的关系, 形成一对铰链函数。针对每一个变量形成铰链函数, 建立分段线性模型, 每个铰链函数拟合原始数据的一部分, 且相互不发生影响。通过反复的穷举搜索, 寻找拟合最好的切分点, 完成全部预测变量的拟合后, 移除其中对模型没有显著贡献的变量, 优选出最合适的模型。MARS方法需要设定两个调优参数, 为预测变量的阶数degree和保留特征的项数nprune。degree为大于或等于1的整数, 较高的阶数会导致计算量大幅度增加, 并导致数值大幅度膨胀或缩小, 不适宜取值过大; nprune一般取值大于或等于2, 当变量数小于10个时, 其上限建议为20[12, 13]。通过模型训练, 获得的调优参数见表1。从表1中可以看出, 硅质矿物的效果最差, r2仅为0.80, TOC和黏土矿物相对较好, r2达到0.92。

表1 基于多元自适应回归样条算法的模型调优参数

2.2.3 神经网络算法

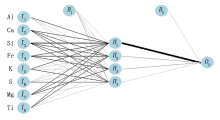
神经网络算法(NN)非常多, 其中前馈神经网络算法最常用。前馈神经网络中各个神经元按接收信息的先后分为不同的组, 每一组可以看作一个神经层。每一层中的神经元接收前一层神经元的输出, 并输出到下一层神经元, 整个网络中的信息是朝一个方向传播, 没有反向的信息传播。前馈神经网络可以看作是一个函数, 通过简单非线性函数的多次复合, 实现输入空间到输出空间的复杂映射。这种网络结构简单, 易于实现[10, 12]。考虑到时效性, 本次研究采用3层神经网络结构, 如图2所示。图2中:前馈神经网络算法里, I1, I2, …, I8为输入层, 代表各个元素数据; H1, H2, H3, H4为隐藏层; O1为输出层; B1和B2为各层的系数。

图2 基于神经网络算法的三层结构示意

设定初始随机数权值和最大迭代次数后, 需要确定调优参数为隐蔽单元个数(size)和权值衰减参数(decay)[10, 12], 通过训练后得到的最佳参数如表2所示。整体而言, 神经网络算法效果较好, r2介于0.88~0.95之间。

表2 基于神经网络算法的模型调优参数
2.3 算法效果对比

三种算法的拟合度(r2)对比如表3所示。三种机器学习算法获得的结果均明显高于常规方法, 效果最差的为硅质矿物, r2为0.80~0.88, MARS算法计算的DEN的r2也不高(为0.85), 其他参数的拟合度均高于0.90。比较而言, MARS算法的整体效果均略低于其他两种算法, SVM算法获得的DEN和TOC效果最佳, 而SVM算法和NN算法获得的黏土矿物、硅质矿物、碳酸盐矿物效果一致。这表明, 整体而言SVM算法效果最佳, 是首选的机器学习算法。

表3 三种算法的拟合度(r2)对比
3 应用效果

将本文建立的参数计算模型在威远、永川工区共28口井进行了应用, 下面以A 9井为例分析应用效果。

A 9井是部署在川西南坳陷白马镇向斜的一口开发评价井, 应用基于支持向量机算法的相关模型, 计算得到黏土矿物、碳酸盐矿物、硅质矿物、TOC和DEN参数, 将计算结果与特殊测井等同类参数进行对比, 如图3所示。标注SVM的图道是本次研究建立的模型计算结果, 未标注的是其他方法获取的同类参数, 其中TOC来源于岩石热解录井, DEN来源于常规测井, 黏土矿物、碳酸盐矿物、硅质矿物数据来源于斯伦贝谢Litho Scanner测井。

图3 A 9井计算参数与实测对比图

从图3可以看出, 大部分井段应用SVM算法计算的DEN、TOC与其他方法获得的结果趋势基本一致, 两者整体相关性较好, r2均为0.85。部分井段计算值与实测值有一定误差, 如3 676.00~3 694.50 m井段DEN实测平均值2.503 g/cm3、计算平均值2.500 g/cm3, TOC实测平均值3.755%、计算平均值3.422%, 计算值略小于实测值, 但绝对值相差较小。在3 696.10 m等井深实测DEN、TOC曲线表现为小尖峰, 但计算的DEN和TOC由于元素录井采样间隔较大, 这一特征并不明显。在岩石成分方面, 计算的黏土矿物与实测黏土矿物差别不大, 仅少部分井段有所差异, r2达到0.86。碳酸盐矿物整体也基本一致, r2可达到0.83, 个别井段有差别, 如在3 668.50~3 670.50 m井段实测碳酸盐矿物有所升高, 但其计算值未体现这一特征。计算的硅质矿物在上部井段整体要大于实测硅质矿物, 且该段计算的硅质矿物值变化不大, 较实测值有所差异, 导致硅质矿物的相关性要略低于前两种矿物。在下部井段, 即水平钻井的目的层段, 计算的硅质矿物与实测吻合度有所提高, r2为0.81。

由于受到岩屑代表性的影响, 以及不同的元素分析仪器导致测量精度存在一定的差异, 基于机器学习算法建立的计算模型, 在应用过程中相关性有所降低, 但r2也达到了0.81~0.86, 应用效果较好。

4 认识与建议

(1)通过分析主要机器学习算法的原理与适用场景, 优选并建立了基于支持向量机、多元自适应回归样条、神经网络算法的参数计算模型, 其中支持向量机算法效果更佳。

(2)应用基于机器学习算法建立的模型, 计算准确性较好, 可解决页岩气井随钻评价参数匮缺的问题, 为页岩气随钻分析与评价提供技术手段。

(3)机器学习算法在解决非线性、复杂模型的建模过程中具有明显优势, 但部分参数的计算精度还有提升空间, 因而有必要进一步加强研究, 挖掘更多录井数据的价值, 扩展到含气量、孔隙度、岩石力学等其他参数, 更好地支撑页岩气的快速评价与压裂测试选层。

编辑 王丽娟

参考文献
[1] 武恒志, 熊亮, 葛忠伟, 等. 四川盆地威远地区页岩气优质储层精细刻画与靶窗优选[J]. 天然气工业, 2019, 39(3): 11-20.
WU Hengzhi, XIONG Liang, GE Zhongwei, et al. Fine characterization and target window optimization of high-quality shale gas reservoirs in the Weiyuan area, Sichuan Basin[J]. Natural Gas Industry, 2019, 39(3): 11-20. [本文引用:3]
[2] 董大忠, 高世葵, 黄金亮, 等. 论四川盆地页岩气资源勘探开发前景[J]. 天然气工业, 2014, 34(12): 1-15.
DONG Dazhong, GAO Shikui, HUANG Jinliang, et al. A discussion on the shale gas exploration & development prospect in the Sichuan Basin[J]. Natural Gas Industry, 2014, 34(12): 1-15. [本文引用:2]
[3] 王玉满, 董大忠, 李建忠, 等. 川南下志留统龙马溪组页岩气储集层特征[J]. 石油学报, 2012, 33(4): 551-561.
WANG Yuman, DONG Dazhong, LI Jianzhong, et al. Reservoir characteristics of shale gas in Longmaxi Formation of the Lower Silurian, southern Sichuan[J]. Acta Petrolei Sinica, 2012, 33(4): 551-561. [本文引用:2]
[4] 涂乙, 邹海燕, 孟海平, 等. 页岩气评价标准与储集层分类[J]. 石油与天然气地质, 2014, 35(1): 153-158.
TU Yi, ZOU Haiyan, MENG Haiping, et al. Evaluation criteria and classification of shale gas reservoirs[J]. Oil & Gas Geology, 2014, 35(1): 153-158. [本文引用:1]
[5] 乔辉, 贾爱林, 贾成业, 等. 页岩气储层关键参数评价及进展[J]. 地质科技情报, 2018, 37(2): 157-164.
QIAO Hui, JIA Ailin, JIA Chengye, et al. Research progress in key parameters of shale gas reservoir evaluation[J]. Geological Science and Technology Information, 2018, 37(2): 157-164. [本文引用:3]
[6] 万金彬, 李庆华, 白松涛. 页岩气储层测井评价及进展[J]. 测井技术, 2012, 36(5): 441-447.
WAN Jinbin, LI Qinghua, BAI Songtao, Well-logging evaluation in shale gas reservoir and its advances[J]. Well Logging Technology, 2012, 36(5): 441-447. [本文引用:3]
[7] 赵红燕, 崔启亮, 石文睿, 等. 涪陵页岩气录井解释评价关键技术[J]. 江汉石油职工大学学报, 2015, 28(3): 28-31.
ZHAO Hongyan, CUI Qiliang, SHI Wenrui, et al. Key technology for evaluating logging interpretation of Fuling shale gas[J]. Journal of Jianghan Petroleum University of Staff and Workers, 2015, 28(3): 28-31. [本文引用:1]
[8] 唐谢, 唐家琼, 庞江平, 等. 长宁地区页岩储集层录井随钻解释评价方法[J]. 录井工程, 2015, 26(4): 11-16.
TANG Xie, TANG Jiaqiong, PANG Jiangping, et al. Mud logging while drilling interpretation and evaluation method for shale reservoir in Changning area[J]. Mud Logging Engineering, 2015, 26(4): 11-16. [本文引用:2]
[9] 顾炎午, 唐诚, 王崇敬, 等. XRF元素录井用于随钻开展页岩评价参数计算的方法[J]. 录井工程, 2018, 29(1): 47-52.
GU Yanwu, TANG Cheng, WANG Chongjing, et al. XRF element logging method for calculating shale evaluation parameters while drilling[J]. Mud Logging Engineering, 2018, 29(1): 47-52. [本文引用:3]
[10] (加)韩家炜, 堪博. 数据挖掘: 概念与技术(原书第2版)[M]. 范明, 孟小峰, 译. 北京: 机械工业出版社, 2007.
(Canada)HAN J W, KAMBER M. Data Mining: Concepts and Techniques(original book 2nd ed. )[M]. FAN Ming, MENG Xiaofeng, trans. Beijing: China Machine Press, 2007. [本文引用:6]
[11] 王志战. 国内非常规油气录井技术进展及发展趋势[J]. 石油钻探技术, 2017, 45(6): 1-7.
WANG Zhizhan. Technical progress and developing trends in unconventional oil and gas mud logging in China[J]. Petroleum Drilling Techniques, 2017, 45(6): 1-7. [本文引用:1]
[12] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
ZHOU Zhihua. Machine learning[M]. Beijing: Tsinghua University Press, 2016. [本文引用:6]
[13] 欧传根, 唐诚, 王崇敬, 等. 基于多元自适应回归样条的页岩密度计算模型[J]. 录井工程, 2021, 32(1): 1-5.
OU Chuangen, TANG Cheng, WANG Chongjing, et al. Shale density calculation model based on multivariate adaptive regression splines[J]. Mud Logging Engineering, 2021, 32(1): 1-5. [本文引用:1]