潜山最早是指一种古地貌特征, 由Powers在20世纪20年代提出^[1], 后来地质学家沿用这一概念, 使用潜山表示在接受沉积之前已经形成的基岩古地貌山, 后被新地层覆盖形成的深埋地下潜伏山。潜山油气藏在纵向上具有明显的分带性, 通常可分为 “ 风化壳带” “ 过渡带” 和“ 潜山内幕” , 储层类型由孔隙型逐渐过渡为裂缝型。

裂缝作为潜山储层中的重要储集空间和主要渗流通道, 在潜山内幕储层的评价中具有重要作用, 其有效性将直接影响产能^{[2, 3, 4, 5, 6]}, 前人对此进行了大量的研究与探索。常规测井识别裂缝主要依赖深、浅双侧向电阻率幅度差异和三孔隙度测井曲线^{[7, 8, 9]}。非常规测井中电成像测井和声波测井是裂缝识别的主要手段。电成像测井依靠分辨率高和直观的优点成为各油田研究裂缝的主流技术^{[10, 11, 12]}, 但贴靠井壁的测量方式让其受到井况和探测深度的制约。利用声波测井识别裂缝的技术近年来发展迅速^{[13, 14]}, 其最大优势是探测范围大, 能填补常规测井资料与地震资料间的空缺, 对井间裂缝的识别具有重要意义。由于潜山储层埋藏深、地层压力大等特点, 深部地层发育的裂缝宽度一般在微米级, 加之空间发育的随机性, 给测井识别带来很大困难。

导电效率最早由Herrick等^[15]提出, 它能反映岩石综合导电能力, 且受地层非均质性影响小, 广泛应用于碳酸盐岩储层饱和度模型的建立^{[16, 17]}。高楚桥等^[18]最早提出用岩石导电效率区分碳酸盐岩储层类型的原理和方法, 并指出裂缝型储层导电效率高, 孔洞型储层导电效率低。本文推导了储层导电效率与裂缝形态的关系表达式, 并针对潜山裂缝型储层的特点, 提出了利用导电效率识别潜山储层裂缝类型的方法。将该方法用于某地区潜山裂缝型储层, 实例应用与理论分析结果相符。

假设在对岩石施加电压时, 岩石消耗的平均电功率为P_t。标准毛管为全含水直毛管, 其长度、含水体积以及水的矿化度均与上述岩石相同, 在同样的电压下标准毛管消耗的电功率为P_s。标准毛管是相同长度、相同含水体积以及相同水矿化度条件下, 导电性最强的情况, 即消耗功率最大的情况。岩石的导电效率即为P_t与P_s之比:

E= PtPs(1)

式中:P_t和P_s分别为在相同电势差下岩石和标准毛管消耗的功率, W; E为岩石的导电效率, 无量纲。

当岩石中不含地层水以外的导电组分时(如黏土和导电矿物), 其导电效率应满足0≤ E≤ 1。

对均匀各向同性且仅地层水导电的岩石, 岩样和标准毛管的长度相同, 施加电压后, 岩石和标准毛管消耗的平均功率分别为:

P_t= U2RtL/At(2)

P_s= U2RwL/As(3)

将公式(2)、(3)带入公式(1), 可得:

E= RwRtLAtLAs= RwRtVtVs(4)

上述式中:U为在两段施加的电压, V; A_t为岩石横截面积, m^②; A_s为标准毛管横截面积, m^②; L为岩石、标准毛管的长度, m; R_t为岩石电阻率, Ω·m; R_w为地层水电阻率(同时也是标准毛管的电阻率), Ω·m; V_t为岩石的体积, m^③; V_s为标准毛管的体积, m^③。

含水孔隙度可以表示为岩石孔隙度与含水饱和度之积, 即ϕ _w=ϕ S_w。又因为标准毛管的体积与岩石含水体积相等, 所以含水孔隙度也可以表示为标准毛管的体积与岩石体积之比, 即ϕ _w=V_s/V_t。将这一转换关系带入公式(4), 可得到岩石导电效率的测井计算公式为:

E= RwRtϕw= RwRtϕSw(5)

式中:ϕ 和S_w分别为岩石孔隙度和含水饱和度, %, 可通过常规测井资料解释获得。

从导电效率的定义可知, 对于仅地层水导电的岩石, 导电效率是表征岩石孔隙中导电流体几何形态的参数。在复杂孔隙储层中, 岩石的储集空间类型直接控制岩石中地层水的分布形态, 故不同类型储集空间对导电效率的影响也不同, 这也是通过导电效率区分储层类型的理论基础。

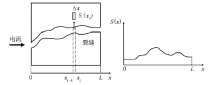
如图1所示, 假设有一边长为L的正方体岩石, 岩石中存在一条不规则裂缝, 裂缝中充满电阻率为R_w的地层水。令电流方向为x轴, 岩石模型的x坐标为[0, L]。设在垂直于x轴的平面上, 岩石的孔隙面积(也是裂缝的截面积)为截面积函数S(x)(x∈ [0, L])。

图1

	Figure Option ViewDownloadNew Window
	图1 发育裂缝的岩石模型

将区间[0, L]分成n个长度相等的子区间[x₀, x₁], (x₁, x₂], (x₂, x₃], …, (x_n-1, x_n], 其中x₀=0, x_n=L, 每个区间的长度均为Δ x=L/n。在第i(i=1, 2, …, n)个子区间上, 岩石的含水体积等于截面积函数的值S(x_i)与区间长度Δ x乘积, 则对所有区间的含水体积求和就得到岩石总的含水体积(同时也是标准毛管的体积), 其公式为:

V_w=V_s= ∑i=1nS(x_i)Δ x= ∫L0S(x)dx(6)

在岩石模型中仅地层水导电, 在第i个区间(x_i-1, x_i]上, 电阻率R_ti与区间长度Δ x和地层水电阻率R_w成正比, 与含水截面积S(x_i)成反比:

R_ti=R_w ΔxS(xi)(7)

岩石总电阻率R_t为所有子区间电阻率R_ti的串联:

$R_{\mathrm{t}}=\sum_{i=1}^{n} \frac{R_{\mathrm{w}}}{\mathrm{S}\left(x_{i}\right)} \Delta x=R_{\mathrm{w}} \int_{0}^{L} \frac{1}{S(x)} \mathrm{d} x$(8)

岩石的总体积V_t=L³, 将公式(6)、(8)和V_t带入式(4)可得到岩石模型的导电效率为:

$E=L^{3} / \int_{0}^{L} S(x) \mathrm{d} x \cdot\left(L^{3} / \int_{0}^{L} \frac{1}{S(x)} \mathrm{d} x\right)$ (9)

公式(9)中L³/ ∫L0S(x)dx为岩石含水孔隙度的倒数$\frac{1}{\phi_{\mathrm{w}}} ; \int_{0}^{L} \frac{1}{S(x)} \mathrm{d} x$表征岩石孔隙空间的复杂程度。

孔隙空间越接近标准毛管, S(x)随x的分布就越均匀, 该值越小; 孔隙空间越复杂, S(x)随x的分布就越不均匀, 该值越大。即储层孔隙结构越复杂, 其导电效率E值越小。

在公式(9)的基础上使用数值模拟的方法研究导电效率与裂缝形态关系, 关键问题是确定截面积函数S(x)的表达形式。较为理想的S(x)函数表达式中需要包含岩石孔隙度大小及裂缝复杂程度两个参数。

为了满足以上条件, 本文使用正弦函数加常数的模型模拟岩石裂缝的截面积函数S(x)。这一数学模型存在三个关键参数, 即正弦函数的周期、振幅和常数项。为研究方便可令函数的周期与岩石长度相等, 此时岩石的孔隙度大小由常数项决定, 裂缝复杂程度由振幅决定。设岩石裂缝截面积函数S(x)为:

S(x)=Asin( 2πLx)+hL (10)

式中:A为正弦函数的振幅, m²; h为裂缝的平均宽度, m。

因此, 裂缝的平均截面积为hL, 岩石的孔隙度为hL²/L³。为保持单位的一致性, 截面积函数S(x)中的常数项设置为hL; 为确保截面积函数非负, 振幅A应满足A∈ [0, hL]。

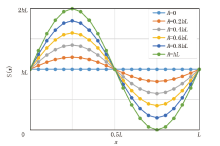
函数S(x)随x的变化如图2所示。常数项hL决定了岩石孔隙度的大小hL²/L³; 而振幅A表示裂缝系统的复杂程度, A值越小裂缝越平直。当A=0时, 裂缝可看作一条标准毛管, 此时岩石的导电效率E应为1; 当A=hL时, S(x)在3/4周期处存在极小值0, 裂缝中的水将被不导电的骨架隔离开, 此时岩石系统中的孔隙为孤立孔隙, 岩石几乎不导电, 导电效率E趋于0。

图2

	Figure Option ViewDownloadNew Window
	图2 用三角函数模拟岩石截面积函数

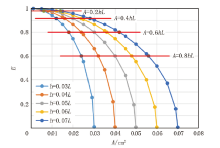
令L=1 cm, 利用公式(9), 分别模拟裂缝平均宽度h为0.03L、0.04L、0.05L、0.06L和0.07L时导电效率E随振幅A的变化规律, 如图3所示。从图中可以看出:(1)随着A的增大, 导电效率E快速下降, 且A接近hL时, 导电效率E接近0(图2水平线; (2)对全含水岩石, 当振幅A分别为0.2 hL、0.4 hL、0.6 hL和0.8 hL时(即裂缝形态相同, 但孔隙度大小不同 ), 不同孔隙度的岩石其导电效率E都相等。

图3

	Figure Option ViewDownloadNew Window
	图3 导电效率E与A和h的关系

由以上结果分析可得:在裂缝型储层中, 影响岩石导电效率的主要因素是裂缝形态, 裂缝越平直, 导电效率越高; 裂缝形态越复杂, 导电效率越低。对全含水岩石, 裂缝孔隙度不直接影响岩石导电效率。

实际情况中, 导电效率往往与孔隙度有较强的相关性。这是由于孔隙度较小的储层孔隙结构通常较差, 如孔隙喉道减小、裂缝闭合等情况都会影响岩石中水的连通性, 从而减小岩石导电效率值。

分析岩心薄片资料发现, 研究区前古近系基岩潜山储层主要发育网状裂缝和溶蚀扩大缝(图4)。对于主要发育网状裂缝的储层, 由于潜山储层埋藏深、地层压力大的特点, 其裂缝宽度一般在微米级, 这些裂缝在宽度最小处几乎闭合。若用公式(10)描述该类储层, 则S(x)的极小值接近甚至等于0, 储层的导电效率E也接近0。对于主要发育溶蚀扩大缝储层, 溶蚀作用主要从两方面影响裂缝的形态:(1)沿裂缝整体溶蚀, 扩大裂缝的张开度, 改善储层的储集性和渗透性。薄片分析资料上表现为溶蚀扩大缝的裂缝张开度明显大于网状裂缝, 孔隙空间的连续性更好; (2)沿裂缝形成溶蚀孔洞, 改善储层的储集性。薄片分析资料上可观察到沿裂缝发育的溶蚀孔洞, 且溶蚀斑块的尺寸远大于裂缝宽度。若同样用公式(10)描述该类储层, 由于溶蚀孔洞的存在, 其裂缝形态不均匀, A值接近h。但由于溶蚀作用对裂缝整体的改善作用, 该类储层的截面积函数S(x)的极小值不为0。

图4

	Figure Option ViewDownloadNew Window
	图4 花岗岩潜山储层岩石薄片特征

从理论上分析, 发育溶蚀扩大缝的储层其导电效率E很小, 但明显大于发育网状裂缝的储层。

图5为研究区X 1井潜山花岗岩裂缝型储层导电效率处理成果图。该井2 828~2 835 m井段和 844~2 851 m井段发育溶蚀扩大缝, 对应电成像图像上能观察到, 溶蚀扩大缝整体的裂缝宽度明显大于网状裂缝, 且沿裂缝发育的溶蚀孔洞尺寸远大于其裂缝宽度。2 835~2 844 m井段发育网状裂缝, 电成像图像上能观察到多条裂缝相互交织, 在裂缝宽度最小处裂缝近乎闭合。利用常规测井曲线, 使用公式(5)计算得到未发生溶蚀现象的储层2号层的导电效率仅为0.004 1, 接近0。发育溶蚀扩大缝的储层, 即1号、3号和4号层的的导电效率分别为0.042、0.024 4和0.0214, 明显大于2号层。该方法用于研究区3口井的潜山裂缝型储层的储集空间类型识别, 得到各层段参数的统计结果, 如表1所示。在研究区发育网状裂缝的储层导电效率通常小于0.02, 而发育溶蚀扩大缝的储层导电效率均大于0.02, 两者区分明显, 且实际计算结果与理论分析规律相符。

图5

	Figure Option ViewDownloadNew Window
	图5 X 1井潜山储层导电效率处理成果

表1

表1

表1 研究区潜山裂缝型储层储集空间类型与导电效率统计 井号 深度/m 孔隙度/ % 岩石电阻率 /(Ω·m) 含水饱和度 /% 地层水电阻率 /(Ω·m) 导电 效率 储集空间 类型 X 1 2 828.1~2 834.4 11.3 25.59 49.95 0.065 0.045 0 溶蚀扩大缝 X 1 2 845.0~2 847.4 7.44 88.7 40.37 0.065 0.024 4 溶蚀扩大缝 X 1 2 848.8~2 850.3 7.32 77.51 49.59 0.065 0.023 1 溶蚀扩大缝 X 2 2 929.2~2 933.9 8.56 27.56 36.45 0.065 0.075 6 溶蚀扩大缝 X 2 2 936.3~2 948.5 8.13 19.57 79.17 0.065 0.051 6 溶蚀扩大缝 X 3 3 301.5~3 309.0 5.62 62.35 44.38 0.065 0.041 8 溶蚀扩大缝 X 3 3 332.7~3 339.8 9.8 38.73 46.28 0.065 0.037 0 溶蚀扩大缝 X 3 3 358.5~3 365.2 7.17 39.27 38.86 0.065 0.059 4 溶蚀扩大缝 X 1 2 835.7~2 845.0 3.63 391.79 74.92 0.065 0.006 1 网状裂缝 X 2 2 966.8~2 971.5 5.04 144.55 66.58 0.065 0.013 4 网状裂缝 X 2 2 995.5~3 008.7 7.65 68.17 61.10 0.065 0.020 4 网状裂缝 X 3 3 372.6~3 375.9 6.5 179.64 39.20 0.065 0.014 2 网状裂缝 X 3 3 385.8~3 387.0 3.32 358.44 41.38 0.065 0.013 2 网状裂缝 X 3 3 396.0~3 397.1 6.27 159.52 52.41 0.065 0.012 4 网状裂缝

表1 研究区潜山裂缝型储层储集空间类型与导电效率统计

(1)本文利用微积分的思想从理论上推导出导电效率与裂缝形态的关系表达式, 并使用正弦函数加常数的模型模拟岩石裂缝形态, 通过数值模拟得到裂缝形态与导电效率的理论关系, 即在裂缝型储层中, 孔隙度的大小不直接影响导电效率, 影响岩石导电效率的主要因素是裂缝形态:裂缝越平直, 导电效率越高; 裂缝形态越复杂, 导电效率越低。

(2)利用裂缝形态与导电效率的理论关系, 结合研究区潜山储层中溶蚀作用对储层的影响, 给出理论分析结果, 即对不发育溶蚀现象的储层, 受潜山储层埋藏深、压力大的影响, 其导电效率接近0; 对于发育溶蚀的储层, 溶蚀现象能有效改善储层的储渗性能, 但溶蚀孔洞的存在会增加裂缝的复杂程度, 降低岩石的导电效率, 故该类储层导电效率不高但明显大于未发生溶蚀现象的储层。将这一认识用于研究区潜山储层, 能有效识别网状裂缝和溶蚀扩大缝, 为潜山裂缝型储层的有效性评价提供依据。

编辑: 卜丽媛