引用本文
金力新, 徐声驰, 郑以华, 刘洋, 王斌, 蒋勇. 阜康凹陷二叠系多成因机制地层异常高压预测方法研究与应用[J]. 录井工程, 2023,34(1): 113-120.
JIN Lixin, XU Shengchi, ZHENG Yihua, LIU Yang, WANG Bin, JIANG Yong. Research and application of prediction method for abnormal high pressure in Permian polygenetic mechanism formation, Fukang sag[J]. Mud Logging Engineering, 2023,34(1): 113-120.
Doi:10.3969/j.issn.1672-9803.2023.01.018  
Permissions
Copyright©2023, 《录井工程》杂志社
《录井工程》杂志社 所有
阜康凹陷二叠系多成因机制地层异常高压预测方法研究与应用
金力新①, 徐声驰②, 郑以华①, 刘洋②, 王斌②, 蒋勇①
①中国石油新疆油田公司勘探事业部
②中国石油西部钻探录井工程分公司

作者简介：金力新 高级工程师,1968年生,1988年毕业于西南石油大学石油地质勘探专业,现在中国石油新疆油田公司勘探事业部从事钻井地质工作。通信地址：834000 新疆克拉玛依市迎宾路66号。电话：13909903385。E-mail：jinlx@petrochina.com.cn

收稿日期: 2022-12-28
摘要

准噶尔盆地阜康凹陷深层勘探程度低,异常高压发育,成因机制多样,传统的钻前地层压力预测方法精度低,难以满足深层油气钻探工程需求。为此,通过分析该区域地层异常高压成因,根据不同高压成因引入地层压力成因修正因子对原伊顿公式进行改进,并建立三维地层压力预测模型。该方法在钻前地层压力预测中应用结果表明,其预测精度达到90%以上,能够满足油气勘探中深层或超深层地层压力预测精度需求。

关键词: 异常高压; 成因机制; 伊顿法; 地层压力; 三维模型; 阜康凹陷
中图分类号:TE132.1 文献标志码:A
Research and application of prediction method for abnormal high pressure in Permian polygenetic mechanism formation, Fukang sag
JIN Lixin①, XU Shengchi②, ZHENG Yihua①, LIU Yang②, WANG Bin②, JIANG Yong①
①Exploration Division of PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China
②CNPC XDEC Geological Research Institute,Karamay,Xinjiang 834000,China
Abstract

The deep exploration degree of Fukang sag in Junggar Basin is low, abnormal high pressure is developed, and the genetic mechanism is diverse. The traditional prediction method of formation pressure before drilling has low accuracy, which is difficult to meet the needs of deep oil and gas drilling engineering. Therefore, by analyzing the formation abnormal high pressure in this area, this paper introduces the formation pressure origin correction factor to improve the original Eaton formula according to different high pressure causes, and establishes a three-dimensional formation pressure prediction model. Applying this method to the prediction of formation pressure before drilling, the results show that the prediction accuracy is over 90%, which can meet the demand of prediction accuracy of deep or ultra-deep formation pressure in oil and gas exploration.

Keyword: abnormal high pressure; genetic mechanism; Eaton method; formation pressure; three-dimensional model; Fukang sag
0 引言

在油气田勘探开发过程中, 地层压力预测准确与否关系到钻完井的速度与安全, 更关系到钻井液密度与套管程序设计等主要钻井工程参数的合理确定与优选。准噶尔盆地阜康凹陷区块勘探程度低, 精准的钻前地层压力预测对安全钻探至关重要。常用的钻前地层压力预测方法主要基于地震资料, 在求取地震层速度后, 利用伊顿法、Fillippone法等计算地层压力, 而对于该预测方法, 地震层速度的精度和地层压力计算方法的适用性是钻前压力预测精准与否的关键。在地震层速度求取方面, 蔡明华等[1]利用测井资料对波阻抗进行约束来获取层速度; 刘洁等[2]提出了谱反演和波阻抗递推反演相结合的方法来获取层速度; 杜斌山等[3]在叠前地震道集中提取速度, 并利用测井速度进行质量控制, 以便提高地震层速度的精度; 罗亚能等[4]运用波形反演和测井资料提高层速度纵向分辨率。在地层压力计算方法方面, 胡华锋等[5]提出了新的构建正常压实速度趋势线方法, 并结合伊顿法, 建立了对实测压力数据要求更低的模型; 霍进等[6]将三维地应力与水平速度引入伊顿法来计算地层压力; 国春香等[7]利用Fillippone法计算地层压力; 徐新纽等[8]基于伊顿法建立地层压力计算模型; 陈志鹏等[9]根据伊顿法采用纵波时差分析对昭通地区的地层压力进行预测。总之, 以上均为围绕地层压力预测开展的相关研究工作, 然而不同区域构造沉积特征不同, 异常高压形成原因也不同, 故导致每种方法普适性较差。

准噶尔盆地阜康凹陷深层由于多期构造运动、地层快速沉积、煤系储层降低砂岩抗压性、厚层泥岩封闭等因素影响[10, 11], 异常高压主要发育在盆地中部的侏罗系至二叠系底部, 具有压力系数高、超压带顶部有致密封隔层、同一超压系统具有相同顶界埋深的特征[12], 上述方法适用性较差。本文以准噶尔盆地阜康凹陷二叠系乌尔禾组、芦草沟组为重点研究对象, 针对其异常高压形成机制, 深入分析了该区主要勘探目的层地层异常高压形成的主控因素, 并针对地层压力分布特征改进伊顿公式, 引入地层压力修正因子Rn, 同时利用地震法预测研究区浅井深层信息并建立伪井, 运用参数反演技术建立三维地层压力模型, 以期达到提高低勘探程度区域钻前地层压力预测精度的目的。

1 区域地质概况

研究区位于准噶尔盆地中央坳陷阜康凹陷东斜坡带, 南北向受阜康断裂带、白家海凸起夹持, 东部地层超覆于北三台凸起、沙奇凸起（北三台凸起为一持续性的古隆起）：二叠系芦草沟组向构造高部位超覆沉积, 逐渐减薄; 上二叠统上乌尔禾组至下三叠统韭菜园组沉积稳定; 三叠纪末印支运动使该区上三叠统小泉沟群遭到强烈剥蚀, 构造高部位三叠系郝家沟组、黄山街组剥蚀殆尽, 克拉玛依组残存厚度为50~250 m; 燕山Ⅱ 幕构造运动使该区强烈抬升, 侏罗系剥蚀严重, 只残存侏罗系八道湾组, 凸起带东西两翼残存有侏罗系三工河组和西山窑组; 白垩纪末的燕山Ⅲ 幕构造运动较弱, 表现为区域性抬升剥蚀, 白垩系仅上部被剥蚀, 构造较平缓, 断裂不发育, 喜马拉雅运动使该区进一步抬升重塑。总之, 研究区构造沉积演化特征与北三台凸起的形成与演化密切相关, 其中心部位是由石炭系基底古隆起构成的核心部分, 由此向西、西北和西南方向则倾没于阜康凹陷, 从北到南依次发育3个凹槽, 即阜北凹槽、阜中凹槽及阜南凹槽。

2 地层异常高压成因机制分析

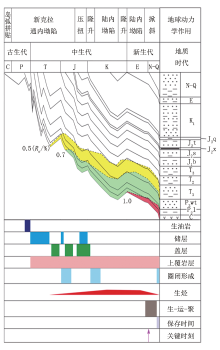
研究区主体上受控于三条大的近北西-南东走向的逆冲断裂（沙丘断裂、B 86井断裂和KT 1井断裂）, 其含油气圈闭主要形成于晚三叠世至早白垩世, 油气运聚主要时期在晚白垩世-新近纪之间（图1）, 由此可见, 圈闭在形成过程中其区域伸展、挤压在空间和时间上的差异性, 导致其复杂的地质构造格局, 同时也导致了油气聚集与调整的差异, 进而形成了独立的超压系统, 异常高压的形成与沉积、构造和油气运聚均有关系[13, 14], 只是其主控因素在不同的地质时代均有不同。

图1 研究区埋藏史及成藏事件

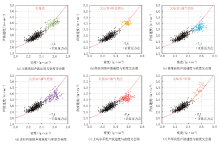
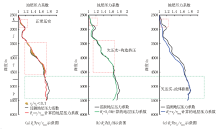
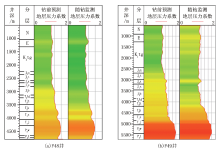
运用Bowers[15]理论建立了加载-卸载曲线方程, 利用声波速度与密度交会确定了研究区地层压力成因呈三段式特征（图2）：一段为吐谷鲁群至侏罗系八道湾组, 为正常压实段; 二段为侏罗系八道湾组至三叠系上统, 该段以欠压实作用为主、局部受构造挤压作用影响（图2a、图2b）; 三段为三叠系中下统至二叠系, 该段以欠压实与流体膨胀共同作用为主, 构造挤压作用为辅（图2c-图2f）。

图2 声波速度与密度交会图

3 传统地层压力预测方法的欠缺

传统利用地震资料预测地层压力的方法有直接预测法、比值法、等效深度法、图板法及原伊顿法, 这些方法没有结合地层压力成因机制, 预测精度低, 且每种方法都有不足之处。直接预测法是利用Fillippone预测模型进行预测, 但该方法仅为一个经验模型, 且模型中孔隙度分别为0和50%时的岩石声速确定较为困难; 比值法和等效深度法是基于建立正常压实趋势线来进行地层压力预测, 但层速度变化趋势受岩性、孔隙及充填流体的影响并非直线; 图板法则通过层速度与地层压力建立的函数关系来预测地层压力, 由于缺少理论基础, 受地质构造影响, 预测精度低; 原伊顿法将测井声波速度替换为地震层速度, 但对正常压实地层的地震层速度难以确定。

本次研究对伊顿公式进行改进, 基于阜康凹陷高压成因机制分析, 引入地层压力修正因子Rn, 通过反算求取不同成因地层压力修正因子的公式, 并分段计算地层压力, 解决了传统方法预测精度低的问题, 通过对原伊顿公式参数进行替换, 提高了公式的可操作性, 并解决了Fillippone预测模型和原伊顿公式参数难以确定的问题。地层压力成因多样, 不同地区地层压力成因不同, 本次研究只针对阜康凹陷欠压实、流体充注和构造挤压三种成因进行改进, 后期可将该方法完善改进后应用到其他区域。

4 多成因机制地层异常高压预测模型的建立
4.1 地震层速度模型的建立

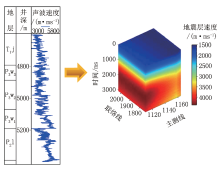
正常压实情况下, 随着埋深的增加和压实作用的增强, 岩石密度随之增大, 同时地层孔隙度降低, 地震波速增大。若地层孔隙中充注着大量气体或液体时, 岩石密度相对减小而孔隙压力增大（即异常高压）, 声波在液体和气体介质中传播的速度要低于在固体介质中传播的速度[17], 因此可通过地震层速度变化预测地层压力的纵向变化规律。目前在缺乏钻井资料的情况下, 通常采用地震速度谱建立层速度模型, 进而预测地层压力, 但地震速度谱分辨率有限, 严重影响压力预测的精度。本文利用测井声波时差富含地层低频和高频信息的特性, 将测井声波时差转换成声波速度, 来约束研究区地震层速度模型（图3）, 可更精确反映出不同深度地层速度的变化, 提高钻前地层压力预测精度。

图3 研究区地震层速度模型

4.2 原伊顿公式改进

伊顿公式是计算地层压力的经典公式, 该公式简单实用, 因而得到广泛的应用, 但其仅适用于基于欠压实理论的地层压力预测, 在研究区应用中存在明显的缺陷和不足：一是研究区深层油气勘探程度较低, 完钻井较少, 测井资料匮乏; 二是伊顿公式中的正常压实声波速度参数依赖室内实验获取, 成本较高; 三是研究区由于受地层压实程度、岩性和孔隙度等因素的影响, 正常地层压力对应低层速度, 使得伊顿公式计算结果误差较大; 四是研究区不同层系单元的地层超压成因不同, 用同一个公式计算地层压力误差较大。原伊顿公式为：

pp=p0-（p0-ph）（v0/vn）N （1）

式中：pp为伊顿公式计算的地层压力系数, 无量纲; p0为上覆岩层压力系数, 无量纲; ph为正常的静水压力系数, 无量纲; v0为实测地层声波速度, m/μ s; vn为正常压实声波速度, m/μ s; N为伊顿指数（该研究区取N=1.2）, 无量纲。

针对原伊顿公式在地层超压预测中存在的缺陷, 在接下来的研究中对该公式进行了改进。由于测井资料缺乏导致声波速度难以获取, 将公式（1）中的v0和vn分别替换为计算点层速度vi和平均速度vii（vii为垂直入射的地震波穿过该界面以上各层的地层总厚度与其总的传播时间之比）, 其中v0≈ vi, vn≈ vii-L。L为vii与vn之间偏移量, m/μ s; 改进后公式为：

px=p0-（p0-ph）（vi/vii）N （2）

$v_{ii}=\sum_{i=1}^{n-1}H_i\bigg/\sum_{i=1}^n T_i$ （3）

式中：px为基于计算点层速度和平均速度的伊顿公式所计算的地层压力系数, 无量纲; vi为计算点层速度, m/μ s; vii为计算点平均层速度, m/μ s; Hi为计算点深度, m; Ti为地震波从地表到计算点深度对应的单趟旅行时间, μ s。

基于修正后的伊顿公式, 引入一个修正因子Rn, 以克服伊顿趋势线因不同成因机制影响地层压力预测精度的问题, 即得到：

p=Rn[p0-（p0-ph）（vi/vii）N] （4）

Rn＝p/px（5）

式中：p为引入地层压力修正因子改进的px计算所得地层压力系数, 无量纲; Rn为地层压力成因修正因子, 无量纲。

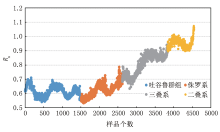
选取研究区域KT 1井侏罗系至二叠系芦草沟组4 546个样点的p和px, 根据公式（5）计算出KT 1井地层压力成因修正因子Rn, 其结果如图4所示。

图4 KT 1井地层压力成因修正因子Rn分布

从图4可以看出, 受同一层系岩石的压实程度、孔隙度、孔隙内充填介质的差异, 以及地震波传播的速度差异性和地震波速度的综合影响, Rn的线性关系较差。KT 1井的Rn值分布特征为：吐谷鲁群和侏罗系集中在0.54~0.7之间（个别值大于0.7）; 三叠系主要集中在0.64~0.95之间, 三叠系中下统局部大于0.9; 二叠系在0.9~1.1之间。结合KT 1井地层压力的三段式成因, 可知不同层系Rn值差异性受地层压力成因机制影响显著。

基于地层异常高压对应地震低层速度的特征, 通过分析KT 1井Rn值与地震层速度、层速度以及深度三者变化规律, 建立研究区域三段压力成因的Rn计算公式。

吐谷鲁群至侏罗系八道湾组（正常压实）的Rn1计算公式为：

Rn1=vi/vmax （6）

侏罗系八道湾组至三叠系上统（欠压实+构造挤压）的Rn2计算公式为：

Rn2=Hi/H （7）

三叠系中下统至二叠系（欠压实+流体膨胀）的Rn3计算公式为：

Rn3=vii/vmax （8）

式中：vmax为最大平均速度, m/μ s; H为最大平均速度对应的深度, m。

上述三个Rn计算公式适用条件为：在三叠系上统以上地层, 当vi/vii< 0.7时, 即为正常压实地层, 公式（6）预测地层压力系数, 与实钻监测结果更吻合（图5a）; 在侏罗系八道湾组至二叠系地层, 当vi/vii≥ 0.7时, 即为欠压实+构造挤压地层, 公式（7）预测地层压力系数与实钻监测误差最小（图5b）; 在三叠系中下统至二叠系地层, 当vi/vii≥ 0.7时, 即为欠压实+流体膨胀地层, 公式（8）预测地层压力系数更符合实钻监测结果（图5c）。

图5 修正因子Rn参数优选

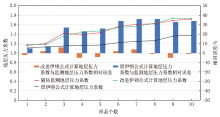
对研究区F 5井原伊顿公式和改进伊顿公式计算的地层压力系数与实钻监测的地层压力系数三者对比分析表明（图6）, 原伊顿公式预测的地层压力系数较实钻监测结果相对误差大于20%, 平均相对误差大于10%; 而改进后的伊顿公式预测结果相对误差小于6%, 平均相对误差小于3%。因此, 改进后的伊顿公式极大降低了地层压力系数预测结果的误差。

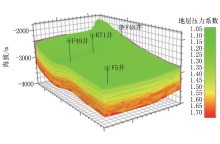
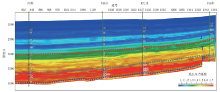
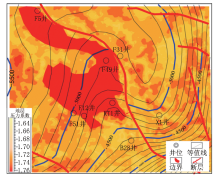
图6 原伊顿公式和改进伊顿公式计算地层压力系数与实钻监测地层压力系数对比

4.3 三维地层压力模型的建立

KT 1井为目前研究区唯一深井, 为增加地层压力模型精度, 利用地震方法预测研究区域内浅井的深层信息, 并建立F 5、F 48、F 49井3口伪井。以这4口井为控制井, 通过对研究区地震体主频、有效频带宽度分析, 优选出平滑半径、有效样本数、高通频率、高截频率等参数进行波形反演, 得到研究区三维地层压力系数预测模型（图7）, 从模型中切取过F 5井-F 49井-KT 1井-F 48井地层压力纵向连井剖面（图8）, 分析研究区侏罗系八道湾组至二叠系上乌尔禾组地层压力分布特征（图9）：八道湾组处于地层压力过渡带, 该层系异常高压主要由于欠压实形成, 地层压力系数为1.15~1.25, KT 1井至F 49井区域受B 86井断裂和局部小断裂挤压, 地层压力系数略高, 为1.20~1.25; 上乌尔禾组整体呈现异常高压特征, 地层压力系数在1.55~1.60以上, 两个逆冲断裂（B 86井断裂和KT 1井断裂）所夹持的鼻状构造带主体部位为超高压区, 地层压力系数为1.76~1.81。应用研究区异常高压成因结合探井试油成果（KT 1、F 49井在上乌尔禾组试油获高产）, 证实超高压区受流体膨胀、构造挤压等作用影响增压明显, 单井目的层地层压力的高低与油气产量呈正相关。通过研究区超高压分布特征预测两个逆冲断裂（B 86井断裂和KT 1井断裂）所夹持的鼻状构造带为油气聚集有利区。

图7 研究区三维地层压力系数预测模型

图8 过F 5井-F 49井-KT 1井-F 48井地层压力纵向连井剖面

图9 侏罗系八道湾组至二叠系上乌尔禾组地层压力分布特征

5 地层压力预测在钻井中的应用

研究区F 48、F 49井, 设计井深分别为4 800、5 770 m, 主要目的层均为二叠系芦草沟组、上乌尔禾组, 利用本文研究成果对F 48、F 49井进行地层压力系数预测（图10）进而指导钻井工程。预测结果表明, F 48井二叠系芦草沟组、上乌尔禾组地层压力系数由三叠系韭菜园组的1.40逐渐抬升至1.61, 为了确保在揭开二叠系高压地层时不发生溢流, 钻揭目的层前建议将设计钻井液密度从1.55 g/cm3提高到1.65 g/cm3左右, 至完钻未出现工程复杂情况; F 49井设计井深5 100 m进入二叠系上乌尔禾组, 预测地层压力系数在井深5 000 m已达到1.50左右。根据前期研究, 该区域从二叠系上乌尔禾组开始的异常高压是因流体膨胀造成的, F 49井二叠系上乌尔禾组预测地层压力系数最大为1.83, 至二叠系芦草沟组地层压力系数开始回落至1.70。现场实钻二叠系上乌尔禾组, 岩性为厚层的砂砾岩, 随钻监测地层压力系数由三叠系韭菜园组的1.50抬升至1.77, 进入超压地层, 钻揭二叠系上乌尔禾组前建议提高钻井液密度至1.82 g/cm3左右, 实际使用钻井液密度为1.80 g/cm3, 未按照原设计继续维持1.70 g/cm3的钻井液密度, 整个钻井过程快速平稳, 未出现复杂情况。

图10 F 48、F 49井钻前预测地层压力系数与随钻监测地层压力系数对比

钻后通过F 48、F 49井钻前模型预测地层压力系数与随钻监测地层压力系数对比（表1）表明：地层压力系数最小误差值0.02, 相对误差值1.76%; 最大误差值0.11, 相对误差值7.97%。在三维地层压力预测模型指导下F 48、F 49井钻井过程中均未发生复杂, 证明本文研究成果和地层压力预测精度可满足该区域钻探需求。

表1 F 48、F 49井钻前模型预测地层压力系数与随钻监测地层压力系数对比
6 结论

（1）研究区地层压力变化极为复杂, 结合岩石属性和加载-卸载理论两种方法进行地层压力成因识别, 研究结果表明, 地层压力呈三段式特征：一段为吐谷鲁群至侏罗系八道湾组的正常压实段; 二段为侏罗系八道湾组至三叠系上统, 该段以欠压实为主、局部受构造挤压影响; 三段为三叠系中下统至二叠系, 该段以欠压实与流体膨胀共同作用为主, 构造挤压为辅。

（2）基于研究区地震及完钻井的测井声波数据, 建立层速度模型, 结合地层压力成因及实钻监测地层压力系数, 提出地层压力成因修正因子Rn改进伊顿公式, 并给出Rn的适用条件, 在研究区的应用结果显示, 改进伊顿公式计算地层压力系数较原伊顿公式计算结果平均相对误差从10%降至3%, 极大提高了地层压力预测精度。

（3）利用地震方法预测研究区浅井的深层信息, 结合已探深井数据, 建立研究区三维地层压力预测模型, 应用研究区异常高压成因结合探井试油成果（KT 1、F 49井在上乌尔禾组试油获高产）, 初步证实超高压区受流体膨胀增压作用明显, 其与欠压实、构造挤压等关系尚需进一步深入研究。

(编辑 唐艳军)

参考文献
[1] 蔡明华, 胡道雄, 蒲国强, 等. 构造应力补偿地层压力预测方法探讨[J]. 新疆石油地质, 2012, 33(4): 507-508.
CAI Minghua, HU Daoxiong, PU Guoqiang, et al. Approach to prediction method for tectonic stress compensating formation pressure[J]. Xinjiang Petroleum Geology, 2012, 33(4): 507-508. [本文引用:1]
[2] 刘洁, 张建中, 孙运宝, 等. 基于地震谱反演的地层速度估算方法及应用[J]. 石油地球物理勘探, 2016, 51(5): 909-915.
LIU Jie, ZHANG Jianzhong, SUN Yunbao, et al. Formation velocity estimation method based on seismic spectrum inversion and its application[J]. Oil Geophysical Prospecting, 2016, 51(5): 909-915. [本文引用:1]
[3] 杜斌山, 雍学善, 王建功, 等. 测井约束下高精度叠前地震速度预测[J]. 岩性油气藏, 2019, 31(4): 92-100.
DU Binshan, YONG Xueshan, WANG Jiangong, et al. High precision prestack seismic velocity prediction based on well logging constraint[J]. Lithologic Reservoirs, 2019, 31(4): 92-100. [本文引用:1]
[4] 罗亚能, 黄捍东, 王玉梅, 等. 地震波形反演与测井联合的三维建模方法[J]. 石油地球物理勘探, 2016, 51(5): 947-954.
LUO Yaneng, HUANG Hand ong, WANG Yumei, et al. Three-dimensional modeling based on integration of full wave inversion and well logging data[J]. Oil Geophysical Prospecting, 2016, 51(5): 947-954. [本文引用:1]
[5] 胡华锋, 胡起, 林正良. 页岩气储层地层压力预测方法及其在四川盆地的应用[J]. 石油物探, 2018, 57(3): 362-368.
HU Huafeng, HU Qi, LIN Zhengliang. Pore pressure prediction for shale gas reservoirs and its application in the Sichuan Basin, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 362-368. [本文引用:1]
[6] 霍进, 石建刚, 沈新普, 等. 新区块及未钻井深部地层孔隙压力预测方法: 以准噶尔盆地南缘高压气井为例[J]. 天然气工业, 2021, 41(3): 104-111.
HUO Jin, SHI Jiangang, SHEN Xinpu, et al. Pore pressure prediction methods for new blocks and undrilled deep strata: A case study of the high pressure gas wells along the southern margin of the Junggar Basin[J]. Natural Gas Industry, 2021, 41(3): 104-111. [本文引用:1]
[7] 国春香, 郭淑文, 翟桐立, 等. 地震压力系数预测在深层天然气勘探中的应用[J]. 物探与化探, 2017, 41(5): 852-855.
GUO Chunxiang, GUO Shuwen, ZHAI Tongli, et al. The application of prediction of seismic pressure coefficient to deep gas exploration[J]. Geophysical and Geochemical Exploration, 2017, 41(5): 852-855. [本文引用:1]
[8] 徐新纽, 孙维国, 阮彪, 等. 准噶尔盆地达巴松凸起超深井安全快速钻井技术[J]. 钻采工艺, 2019, 42(6): 28-31.
XU Xinniu, SUN Weiguo, RUAN Biao, et al. Safe and fast drilling in ultradeep well at Dabasong uplift, Junggar Basin[J]. Drilling & Production Technology, 2019, 42(6): 28-31. [本文引用:1]
[9] 陈志鹏, 梁兴, 张介辉, 等. 昭通国家级示范区龙马溪组页岩气储层超压成因浅析[J]. 天然气地球科学, 2016, 27(3): 442-448.
CHEN Zhipeng, LIANG Xing, ZHANG Jiehui, et al. Genesis analysis of shale reservoir overpressure of Longmaxi Formation in Zhaotong Demonstration Area, Dianqianbei Depression[J]. Natural Gas Geoscience, 2016, 27(3): 442-448. [本文引用:1]
[10] 易泽军, 何登发. 准噶尔盆地东部构造地层层序及盆地演化[J]. 石油与天然气地质, 2018, 39(5): 932-942.
YI Zejun, HE Dengfa. Tectono-stratigraphic sequence and basin evolution of the eastern Junggar Basin[J]. Oil & Gas Geology, 2018, 39(5): 932-942. [本文引用:1]
[11] 胡海燕, 王国建. 准噶尔盆地中部超压形成机理及其成藏意义[J]. 石油天然气学报(江汉石油学院学报), 2009, 31(1): 6-10.
HU Haiyan, WANG Guojian. Formation mechanism of overpressure in central Junggar Basin and its reservoir-forming significance[J]. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Insitute), 2009, 31(1): 6-10. [本文引用:1]
[12] 查明, 张卫海, 曲江秀. 准噶尔盆地异常高压特征、成因及勘探意义[J]. 石油勘探与开发, 2000, 27(2): 31-35.
ZHA Ming, ZHANG Weihai, QU Jiangxiu. Characteristics, genesis and exploration significance of abnormal high pressure in Junggar Basin[J]. Petroleum Exploration and Development, 2000, 27(2): 31-35. [本文引用:1]
[13] 易泽军. 准噶尔盆地东部二叠系地质结构及成因机制[D]. 北京: 中国地质大学, 2018.
YI Zejun. Geological structure and genetic mechanism of Permian in eastern Junggar Basin[D]. Beijing: China University of Geosciences, 2018. [本文引用:1]
[14] BOWERS, GL. Pore pressure estimation from velocity data: Accounting for overpressure mechanisms besides undercompaction[J]. SPE Drilling & Completion, 1995: 89-95. [本文引用:1]
[15] 周东红, 熊晓军. 一种高精度地震压力预测方法[J]. 石油地球物理勘探, 2014, 49(2): 344-348.
ZHOU Donghong, XIONG Xiaojun. A high-precision seismic pressure prediction method[J]. Oil Geophysical Prospecting, 2014, 49(2): 344-348. [本文引用:1]