基于模糊数学层次分析的井漏地质风险分级定量评价研究

引用本文

邓津辉, 刘广明, 谭忠健. 基于模糊数学层次分析的井漏地质风险分级定量评价研究[J]. 录井工程, 2023,34(1): 40-46.
DENG Jinhui, LIU Guangming, TAN Zhongjian. Study on quantitative evaluation of lost circulation geological risk classification based on fuzzy mathematics analytic hierarchy process[J]. Mud Logging Engineering, 2023,34(1): 40-46.
Doi:10.3969/j.issn.1672-9803.2023.01.007 复制到剪切板

Permissions

《录井工程》杂志社所有

基于模糊数学层次分析的井漏地质风险分级定量评价研究

邓津辉^①, 刘广明^②, 谭忠健^①

①中海石油（中国）有限公司天津分公司

②中海油能源发展股份有限公司工程技术分公司

作者简介：邓津辉高级工程师,1976年生,2002年硕士毕业于中国科学院兰州地质研究所,现主要从事油气勘探地质研究工作。通信地址：300459 天津市滨海新区海川路2121号渤海石油管理局C座。电话：（022）66502287。E-mail：dengjh@cnooc.com.cn

收稿日期: 2023-01-30

摘要

井漏是影响钻井作业最大的风险之一,预防井漏一直是钻井作业不断探索的工作。评价井漏的方式是评价地层漏失通道和漏失空间,即井漏地质风险。建立准确评价地层井漏地质风险的方法,对于指导现场钻井安全工作具有非常重要的意义。由于井漏地质风险自身的不确定性,只能进行定性评价,为使井漏地质风险评价更客观、更具体,实现定量评价,以渤海X油田为例,通过分析发生过漏失井的资料,提出了模糊数学和层次分析相结合定量判断井漏风险的评价方法,实现了钻前井漏地质风险定性、定量评价。基于模糊数学层次分析方法计算得出井漏地质风险值,建立漏失排量与风险值关系模型,依据计算的风险值,将井漏风险定量划分为高风险、中风险、低风险3个级别,可为井漏风险井的分类提供重要依据。

关键词: 模糊数学; 层次分析方法; 井漏; 地质风险; 定量化评价

中图分类号:TE132.1 文献标志码:A

Study on quantitative evaluation of lost circulation geological risk classification based on fuzzy mathematics analytic hierarchy process

DENG Jinhui^①, LIU Guangming^②, TAN Zhongjian^①

①CNOOC（China） Co., Ltd.,Tianjin Branch, Tianjin 300459, China

②CNOOC Ener Tech-Drilling & Production Co.,Tianjin 300452,China

Abstract

Leakage is one of the biggest risk to be always prevented in the constant exploration of drilling operations. The approach to evaluate well leakage is to evaluate the geological risk of the formation channel loss and space loss. Establishing a method of accurately evaluating the geological risk of the formation loss is of important significance for guiding the safety work of the field drilling. The geological risk of well loss itself is an uncertain concept, which can only be evaluated qualitatively. In order to make the evaluation of well loss geological risk more objective and specific, and realize quantitative evaluation, the author takes Bohai X Oilfield as an example, analyzes the data of wells that have experienced losses, and puts forward the method of quantitative judgment of well loss risk by combining fuzzy mathematics and hierarchical analysis. Finally, the quantitative and qualitative evaluation of geological risk of well loss before drilling is realized. The fuzzy hierarchical analysis method is used to calculate the geological risk value of the well loss, and the relationship model between the leakage rate and the risk value is established. According to the calculated risk value, the well loss risk is quantitatively divided into three levels: high risk, medium risk and low risk, which can provide an important basis for the classification of the well with the risk of loss.

Keyword: fuzzy mathematics; analytic hierarchy process; leakage; geological risk; quantitative evaluation

文章图片

0 引言

井漏是一种在钻井过程中钻井液、水泥浆或其他工作液漏失到地层中的现象, 是钻井过程中常见的井下复杂情况之一, 它不仅耗费钻井时间, 损失钻井液, 而且有可能引起卡钻、井喷、井塌等一系列复杂情况, 甚至导致井眼报废, 造成较大的经济损失^{[1, 2, 3, 4, 5]}, 在现场钻进中, 规避井漏具有重大意义。

钻井是一项隐蔽的地下工程, 其实施过程中发生的井漏问题往往存在着模糊性、随机性和不确定性。判断漏失的方法通常是通过统计前期漏失地层的岩性、漏失工况及漏失通道分析原因^{[6, 7, 8, 9, 10]}, 也可以结合地层力学与物理性质判断漏层特性^{[11, 12, 13]}。本文基于模糊数学层次分析方法计算得出井漏地质风险值, 建立漏失排量与风险值关系模型, 为井漏风险井的分类提供重要依据。

1 模糊数学层次分析方法

1.1 模糊数学理论

在地质学研究领域内, 有很多现象的发生是不确定的, 如沉积岩的沉积相、复杂岩性、圈闭含油气性、含油气面积、断层封闭性等。当想要从定量的角度解决这些地质问题时, 就需要数学与地质相结合。然而, 经典数学又不太适合用于分析、处理地质学中的这类模糊问题, 因此应用模糊数学的方法定量分析、研究、处理地质学中的模糊信息, 具有更大的优越性^[14]。模糊数学是用定量的方法去研究、处理模糊现象的数学分支^[15]。模糊理论是把数学的应用范围从清晰现象扩大到模糊现象, 从中确定广义的排中律— — 隶属规律^[16], 为了实现模糊的井漏地质风险转向定量化评价, 对漏失井的漏失原因进行统计分析, 结合统计规律确定地质元素与井漏风险性的隶属关系, 建立相适应的风险评价标准, 进而建立单井井漏地质风险元素矩阵。

1.2 层次分析方法

层次分析法是美国运筹学家萨蒂于20世纪70年代初为美国国防部研究“ 根据各个工业部门对国家福利的贡献大小而进行电力分配” 课题时, 应用网络系统理论和多目标综合评价方法所提出的一种层次权重决策分析方法。

层次分析法是一种对复杂问题进行预测、决策、计划和系统分析, 将决策者的定性判断和定量计算有效结合起来的决策分析方法。其基本原理为：在系统分析过程中, 把复杂的问题依据问题的性质或需要分解为若干有序层次, 然后再根据对客观现实的认识和判断, 给出每一层次元素间相对重要性的定量表示, 即所谓构造比较判断矩阵, 再依据数学方法求出判断矩阵的最大特征根及其特征向量, 依次确定每一层次内元素间的相对重要性次序的权值^{[17, 18, 19, 20]}。

2 井漏地质风险元素分析

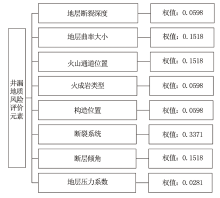
通过对渤海X油田已漏失井主控地质元素统计分析发现, 井漏的发生原因多种多样（表1）。从表1可以看出, 断裂深度、地层曲率、火山通道距离、岩性、构造位置、断裂系统、断层倾角、地层压力系数是相对重要的井漏地质风险元素。

表1 渤海X油田漏失井主控地质元素统计

结合渤海X油田实钻井井漏统计分析建立了井漏地质风险综合评价指标, 并将井漏地质风险划分为低风险、中风险和高风险（表2）。

表2 井漏地质风险划分标准

2.1 层次分析法确定权值

根据渤海X油田的井漏原因统计分析结果, 建立井漏地质风险元素集合, 对集合内每一项元素应用层次分析方法, 结合专家评分进行两两比较, 建立比较判断矩阵M, 计算各元素对应的井漏风险权值。

需要说明的是, 专家经验是建立在对地质背景熟悉的情况下, 不同区块对比结果可能会不同, 例如, 某些区块断层封堵性较好, 断裂系统对于漏失的贡献可能较小; 某些区块开采时间久, 储层存在亏压, 其地层压力对于漏失的贡献可能更大等。笔者所选依据渤海X油田相应地质背景, 亦不能作为统一标准。设井漏地质风险评价元素集合U={地层断裂深度a₁, 地层曲率大小a₂, 火山通道位置a₃, 火成岩类型a₄, 构造位置a₅, 断裂系统a₆, 断层倾角a₇, 地层压力系数a₈}, 并对其各元素采用1~9标度法^{[18, 19]}进行两两对比, 尽可能减少性质不同元素相互比较的困难。用1、3、5、7、9表示两元素之间相对重要程度, 1、1/3、1/5、1/7、1/9表示两元素之间相对不重要程度, 1表示同等重要, 3表示稍微重要, 5表示明显重要, 7表示强烈重要, 9表示极端重要, 其中间值2、4、6、8表示重要性位于其前后两重要性之间^[21], 据此建立比较判断矩阵M（公式1）得到归一化后特征向量ω （公式2）。

由于影响井漏的地质元素复杂, 所给出的判断矩阵不能保证完全一致, 有必要进行一致性检验。由公式Mω =ϕ ω 计算最大特征根ϕ 。依据层次分析表^[19]可知, 随机一致性指标R_I值为1.41, 一致性指标C_I=（ϕ -n）/（n-1）（其中n为地质元素个数）, 随机一致性比率C_R=C_I/R_I, 若C_R< 0.1, 表示一致性通过, 否则应调整元素取值。计算得到C_R=0.015 6, 权值合理。

依据层次分析方法得到权值结果（图1）, 并建立井漏地质风险元素评价矩阵V_M（公式5）。

$M ＝ [\begin{matrix} a_{1} & a_{2} & a_{3} & a_{4} & a_{5} & a_{6} & a_{7} & a_{8} \\ a_{1} & 1 & 1 / 3 & 1 / 3 & 1 & 1 & 1 / 5 & 1 / 3 & 3 \\ a_{2} & 3 & 1 & 1 & 3 & 3 & 1 / 3 & 1 & 5 \\ a_{3} & 3 & 1 & 1 & 3 & 3 & 1 / 3 & 1 & 5 \\ a_{4} & 1 & 1 / 3 & 1 / 3 & 1 & 1 & 1 / 5 & 1 / 3 & 3 \\ a_{5} & 1 & 1 / 3 & 1 / 3 & 1 & 1 & 1 / 5 & 1 / 3 & 3 \\ a_{6} & 5 & 3 & 3 & 5 & 5 & 1 & 3 & 7 \\ a_{7} & 3 & 1 & 1 & 3 & 3 & 1 / 3 & 1 & 5 \\ a_{8} & 1 / 3 & 1 / 5 & 1 / 5 & 1 / 3 & 1 / 3 & 1 / 7 & 1 / 5 & 1 \end{matrix}]$ （1）

$ω ＝ {[\begin{matrix} 0.0598 & 0.1518 & 0.1518 & 0.0598 & 0.0598 & 0.3371 & 0.1518 & 0.0281 \end{matrix}]}^{T}$ （2）

$Mω ＝ {[\begin{matrix} 0.4829 & 1.2462 & 1.2462 & 0.4829 & 0.4829 & 2.7963 & 1.2462 & 0.2271 \end{matrix}]}^{T}$ （3）

$ϕ ＝ \frac{1}{8} (\frac{0.4829}{0.0598} + \frac{1.2462}{0.1518} + \frac{1.2462}{0.1518} + \frac{0.4829}{0.0598} + \frac{0.4829}{0.0598} + \frac{2.7963}{0.3371} + \frac{1.2462}{0.1518} + \frac{0.2271}{0.0281}) ＝ 8.1539$ （4）

$V_{M} ＝ [\begin{matrix} 0.0598 & 0.1518 & 0.1518 & 0.0598 & 0.0598 & 0.3371 & 0.1518 & 0.0281 \end{matrix}]$ （5）

	Figure Option View Download New Window
	图1 井漏地质风险层次分析权值结果

2.2 风险评价赋值标准

为简化计算过程, 结合单井井漏地质风险元素数据, 采用二进制方式进行风险评价赋值, 据此建立风险评价指标矩阵, 根据风险指标低、中、高分别赋分数值1、2、3（表3）, 所用标准赋值矩阵为[1, 2, 3]^T。结合单井井漏地质风险元素数据可建立单井风险评价指标矩阵。

表3 风险评价赋值标准

3 井漏地质风险值分析

通过分析X 34、X 19、X 2、X 13、X 21井的井漏地质风险元素数据（表4）, 依据风险评价赋值标准, 建立5口井的井漏地质风险元素评价指标矩阵R如下：

表4 5口井井漏地质风险元素数据统计

$R_{X 34} ＝ [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{matrix}] ； R_{X 19} ＝ [\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}] ； R_{X 2} ＝ [\begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}] ； R_{X 13} ＝ [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}] ； R_{X 21} ＝ [\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}]$

根据井漏风险元素权重计算5口井井漏地质风险元素评价矩阵如下：

$V_{_{X 34}} ＝ V_{M} \times R_{X 34} ＝ [\begin{matrix} 0.3317 & 0.5167 & 0.1518 \end{matrix}]$

$V_{_{X 19}} ＝ V_{M} \times R_{X 19} ＝ [\begin{matrix} 0.0879 & 0.3036 & 0.6085 \end{matrix}]$

$V_{_{X 2}} ＝ V_{M} \times R_{X 2} ＝ [\begin{matrix} 0.0281 & 0.0000 & 0.9719 \end{matrix}]$

$V_{_{X 13}} ＝ V_{M} \times R_{X 13} ＝ [\begin{matrix} 0.2995 & 0.2116 & 0.4889 \end{matrix}]$

$V_{_{X 21}} ＝ V_{_{M}} \times R_{X 21} ＝ [\begin{matrix} 0.2397 & 0.6407 & 0.1196 \end{matrix}]$

依据风险评价标准赋值矩阵, 进一步求取各井的井漏地质风险值B的计算方法及结果如下：

$\begin{array}{c} B_{\mathrm{x} 34}=\left[\begin{array}{lll} 0.3317 & 0.5167 & 0.1518 \end{array}\right] \times\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]=1.8205 \\ B_{\mathrm{x} 19}=\left[\begin{array}{lll} 0.0879 & 0.3036 & 0.6085 \end{array}\right] \times\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]=2.5206 \\ B_{\mathrm{X} 2}=\left[\begin{array}{lll} 0.0281 & 0.0000 & 0.9719 \end{array}\right] \times\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]=2.9438 \\ B_{\mathrm{x} 13}=\left[\begin{array}{lll} 0.2995 & 0.2116 & 0.4889 \end{array}\right] \times\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]=2.1894 \\ B_{\mathrm{x} 21}=\left[\begin{array}{lll} 0.2397 & 0.6407 & 0.1196 \end{array}\right] \times\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]=1.8799 \end{array}$

由统计的5口井井漏数据及计算得到的井漏地质风险值（表5）可以明显看出, 模糊数学方法计算得到的风险值与钻井发生井漏时的漏速与排量具有高度相关性, 即：风险值高（发生漏失风险高）, 表现为发生漏失时的排量低, 漏速大; 风险值低（发生漏失风险低）, 表现为发生漏失时的排量高, 漏速小。

表5 5口井井漏数据及井漏地质风险值统计

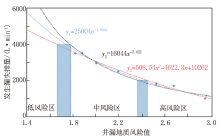
统计渤海X油田6口井7个漏失点的井漏地质风险值与漏失排量, 对其进行回归模型分析（图2）, 为防止出现过拟合情况, 分别应用指数函数、简单幂函数、多项式进行井漏地质风险值与漏失排量之间的回归拟合, 模型公式及经验损失值分别为：

$y_{1} ＝ 25004 e^{- 1.054 x} R_{emp} ＝ 103.31$ （指数函数）

$y_{2} ＝ 16044 x^{- 2.422} R_{emp} ＝ 132.72$ （幂函数）

$y_{3} ＝ 508.54 x^{2} - 4622.3 x + 10262 R_{emp} ＝ 84.81$ （多项式）

	Figure Option View Download New Window
	图2 井漏地质风险值与发生漏失排量回归学习模型

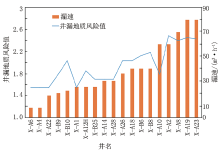
经验损失函数显示应用多项式函数关系拟合方法的相关性最高, 但因样品数量较少, 其准确性存疑。统计渤海X油田漏失井漏失速度与井漏地质风险值进行统计, 从图3可以看出, 井漏地质风险值越大, 漏速越高, 漏失井的井漏地质风险值多大于1.6, 且当井漏地质风险值大于2.4时, 漏速高达70 m³ /h, 风险较高。综合分析图2、图3, 根据现场钻井作业时泥浆泵可用排量, 可以认为2 000~4 000 L/min是钻井常用排量。在常用排量下, 3种模型公式计算井漏地质风险值均为1.6~2.4之间, 模型公式的类型对结果影响较小, 故认为井漏地质风险值在1.6~2.4时为可控风险, 属于中漏失风险, 低于1.6时为低漏失风险, 高于2.4时为高漏失风险。

	Figure Option View Download New Window
	图3 渤海X油田漏失井井漏地质风险值与漏速统计

4 应用效果分析

在渤海油田选取X-5 d井进行井漏预测分析。根据钻前地震资料选取地质元素3个井漏风险点（表6）, 依据井漏地质风险元素划分标准进行X-5 d井井漏风险元素评估。

表6 X-5 d井井漏风险元素数据统计

分别建立3个风险点的井漏地质风险元素评价指标矩阵R₁、R₂、R₃, 并以此计算各风险点井漏地质风险值, 计算结果如下：

$B_{1} ＝ V_{M} \times R_{1} \times {[\begin{matrix} 1 & 2 & 3 \end{matrix}]}^{T} ＝ 1.4830$

$B_{2} ＝ V_{M} \times R_{2} \times {[\begin{matrix} 1 & 2 & 3 \end{matrix}]}^{T} ＝ 1.9995$

$B_{3} ＝ V_{M} \times R_{3} \times {[\begin{matrix} 1 & 2 & 3 \end{matrix}]}^{T} ＝ 2.6683$

实钻结果表明, 本井在风险点1未发生井漏, 在风险点2和风险点3位置发生了漏失。

风险点2位置井漏概况：钻进至3 227.00 m, 返出突然减少, 循环池液面下降, 立即将钻具提离井底, 降低排量, 检查地面管线正常, 确定井下发生漏失, 漏失排量2 960 L/min, 分别以1 500、1 000、800 L/min排量循环测漏速均为48.0 m³ /h。风险点3位置漏失情况如下：四开钻进至3 778.00 m, 返出突然减少, 循环池液面下降, 监测瞬时漏速34.00 m³ /h, 立即将钻具提离井底, 降低排量, 检查地面管线正常, 确定井下发生漏失, 漏失排量1 700 L/min（表7）。

表7 X-5 d井井漏预测及漏失统计

综上对风险评估结果进行讨论：风险点1和风险点2的实钻结果对比发现, 井漏地质风险值能够反映地层发生井漏的风险, 即风险值越大, 井漏风险越大; 但本井风险点2和风险点3位置发生的井漏对比性较差, 原因是两处漏失发生在不同井眼尺寸内, 风险点2井眼为311.15 mm, 风险点3井眼为215.90 mm, 由于风险点3井眼尺寸小于风险点2井眼尺寸, 采用相对低排量即可达到地层最大承受压力, 所以发生漏失时造成排量低、漏速低的情况。

5 结论

（1）利用模糊数学层次分析方法可以实现将不可量化的井漏地质风险定量化, 其用来研究井漏的方向是可行的。

（2）井漏地质风险元素调整需要根据各类地质背景, 由经验丰富的专家进行定性对比, 应用层次分析方法进行定量对比并通过一致性检验其对比结果的权值是否合理。针对渤海X油田复杂地层, 需要通过大量数据研究、分析钻井发生井漏的风险值与排量之间的关系, 后续研究工作适宜结合机器学习方法建立回归模型, 将井漏地质风险与排量关系进一步拟合, 从而指导后续钻井作业。

（3）根据风险指标低、中、高分别赋分数值, 结合单井井漏地质风险元素数据建立单井风险评价指标矩阵, 进一步计算得出各井的井漏地质风险值, 可为井漏风险井的分类提供重要依据。

(编辑张鑫)

参考文献

文献列表

[1]	金衍, 卢运虎, 李再均. 一种井漏层位钻前风险预测新方法[J]. 石油钻采工艺, 2008, 30(3): 24-28. JIN Yan, LU Yunhu, LI Zaijun. A new pre-drilling risk prediction method for lost zone in well[J]. Oil Drilling & Production Technology, 2008, 30(3): 24-28. [本文引用:1]
[2]	《海洋钻井手册》编委会. 海洋钻井手册[M]. 北京: 石油工业出版社, 2009. Editorial Board of Offshore Drilling Manual. Offshore drilling manual[M]. Beijing: Petroleum Industry Press, 2009. [本文引用:1]
[3]	康毅力, 王海涛, 游利军, 等. 基于层次分析法的地层钻井液漏失概率判定[J]. 西南石油大学学报(自然科学版), 2013, 35(4): 180-186. KANG Yili, WANG Haitao, YOU Lijun, et al. Probability determination for loss circulation of drilling fluids based on analytic hierarchy process[J]. Journal of Southwest Petroleum University (Natural Science Edition), 2013, 35(4): 180-186. [本文引用:1]
[4]	范翔宇, 田云英, 夏宏泉, 等. 基于测井资料确定钻井液漏失层位的方法研究[J]. 天然气工业, 2007, 27(5): 72-74. FAN Xiangyu, TIAN Yunying, XIA Hongquan, et al. Research on the method of determining the leakage layer of drilling fluid based on logging data[J]. Natural Gas Industry, 2007, 27(5): 72-74. [本文引用:1]
[5]	郑贵. 井壁稳定问题的断裂损伤力学机理的研究[D]. 哈尔滨: 哈尔滨工程大学, 2005. ZHENG Gui. Study on mechanical mechanism of fracture damage of shaft wall stability problem[D]. Harbin: Harbin Engineering University, 2005. [本文引用:1]
[6]	侯冰, 陈勉, 朱静. 模糊物元方法评价区域漏失分布特征[J]. 石油钻采工艺, 2013, 35(1): 115-117. HOU Bing, CHEN Mian, ZHU Jing. Evaluation of regional leakage distribution characteristics by fuzzy matter-element method[J]. Oil Drilling & Production Technology, 2013, 35(1): 115-117. [本文引用:1]
[7]	侯冰, 陈勉, 卢虎, 等. 库车山前下第三系漏失原因分析及堵漏方法[J]. 石油钻采工艺, 2009, 31(4): 40-44. HOU Bing, CHEN Mian, LU Hu, et al. Analysis of the causes of the paleogene leakage in Kuqa Piedeart and the method of sealing leakage[J]. Oil Drilling & Production Technology, 2009, 31(4): 40-44. [本文引用:1]
[8]	金衍, 陈勉, 刘晓明, 等. 塔中奥陶系碳酸盐岩地层漏失压力统计分析[J]. 石油钻采工艺, 2007, 29(5): 82-84. JIN Yan, CHEN Mian, LIU Xiaoming, et al. Analysis on the leakage pressure of Ordovician carbonate formation in Tazhong area[J]. Oil Drilling & Production Technology, 2007, 29(5): 82-84. [本文引用:1]
[9]	张春阳, 谭强, 邓建明, 等. 地层力学与物理性质联合判断漏层方法及应用[J]. 石油天然气学报, 2009, 31(5): 371-373. ZHANG Chunyang, TAN Qiang, DENG Jianming, et al. Method and application of combining stratigraphic mechanics and physical properties to judge leakage layer[J]. Journal of Oil and Gas Technology, 2009, 31(5): 371-373. [本文引用:1]
[10]	陈钢花, 邱正松, 尹成芳, 等. 井漏层位确定方法探讨[J]. 钻井液与完井液, 2009, 26(2): 56-59. CHEN Ganghua, QIU Zhengsong, YIN Chengfang, et al. Discussion on determination method of well loss zone[J]. Drilling Fluid & Completion Fluid, 2009, 26(2): 56-59. [本文引用:1]
[11]	王眉山. 排量与循环时差法确定漏层位置初探[J]. 钻采工艺, 1997, 20(4): 22-25. WANG Meishan. Preliminary study on determining the location of leakage layer by the method of displacement and cycle time difference[J]. Drilling & Production Technology, 1997, 20(4): 22-25. [本文引用:1]
[12]	李必智. 钻井地质力学模型关键参数计算和应用研究[D]. 西安: 西安石油大学, 2016. LI Bizhi. Calculation and application of key parameters of drilling geomechanical model[D]. Xi'an: Xi'an Shiyou University, 2016. [本文引用:1]
[13]	李大奇. 裂缝性地层钻井液漏失动力学研究[D]. 成都: 西南石油大学, 2012. LI Daqi. Study on fluid loss dynamics in fractured formation[D]. Chengdu: Southwest Petroleum University, 2012. [本文引用:1]
[14]	张强, 孙新亚, 叶晔, 等. 模糊数学在石油地质中的应用综述[J]. 云南化工, 2019, 46(12): 132-134. ZHANG Qiang, SUN Xinya, YE Ye, et al. Application of fuzzy mathematics in petroleum geology[J]. Yunnan Chemical Industry, 2019, 46(12): 132-134. [本文引用:1]
[15]	翟汝霞. 模糊数学应用软件设计及其在地质评价与识别中的应用[D]. 青岛: 中国石油大学(华东), 2008. ZHAI Ruxia. Design of fuzzy mathematics application software and its application in the geologic assessment and recognition[D]. Qingdao: China University of Petroleum(East China), 2008. [本文引用:1]
[16]	宋子齐. 划分油水层的一种模糊数学方法[J]. 西安石油大学学报(自然科学版), 1987, 2(1): 51-63. SONG Ziqi. A fuzzy mathematical method to divide oil and water layers[J]. Journal of Xi 'an Shiyou University (Natural Science), 1987, 2(1): 51-63. [本文引用:1]
[17]	吕彦平, 吴晓东, 李朝霞, 等. 层次分析法在螺杆泵井故障诊断中的应用[J]. 石油钻采工艺, 2008, 30(6): 80-82, 87. LYU Yanping, WU Xiaodong, LI Zhaoxia, et al. Application of analytic hierarchy process in the fault diagnosis of progressing cavity pump well[J]. Oil Drilling & Production Technology, 2008, 30(6): 80-87. [本文引用:1]
[18]	张卓. 基于AHP方法的成员搜索引擎调度策略[J]. 西安石油大学学报(自然科学版), 2014, 29(4): 106-110. ZHANG Zhuo. Scheduling strategy of member search engine based on AHP method[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2014, 29(4): 106-110. [本文引用:2]
[19]	张晓伟, 刘人和. 层次分析法在油页岩选区评价中的应用[J]. 中国石油勘探, 2011, 16(4): 82-86. ZHANG Xiaowei, LIU Renhe. Application of analytic hierarchy process in oil shale selection evaluation[J]. China Petroleum Exploration, 2011, 16(4): 82-86. [本文引用:3]
[20]	贾敏, 张建军, 李隽, 等. 一种气井泡沫排水采气效果模糊定量评价方法[J]. 中国石油勘探, 2017, 22(5): 119-124. JIA Min, ZHANG Jianjun, LI Jun, et al. A fuzzy quantitative evaluation method of foam drainage gas recovery effect in gas well[J]. China Petroleum Exploration, 2017, 22(5): 119-124. [本文引用:1]
[21]	侯海海, 邵龙义, 唐跃, 等. 基于多层次模糊数学的中国低煤阶煤层气选区评价标准: 以吐哈盆地为例[J]. 中国地质, 2014, 41(3): 1002-1009. HOU Haihai, SHAO Longyi, TANG Yue, et al. Selection evaluation criteria for low-rank coal bed methane in China based on multi-level fuzzy mathematics: A case study of Turpan-Hami Basin[J]. Geology In China, 2014, 41(3): 1002-1009. [本文引用:1]

2008

0.0

... 0 引言井漏是一种在钻井过程中钻井液、水泥浆或其他工作液漏失到地层中的现象,是钻井过程中常见的井下复杂情况之一,它不仅耗费钻井时间,损失钻井液,而且有可能引起卡钻、井喷、井塌等一系列复杂情况,甚至导致井眼报废,造成较大的经济损失^[1,2,3,4,5],在现场钻进中,规避井漏具有重大意义 ...

2009

0.0

2013

0.0

2007

0.0

2005

0.0

2013

0.0

... 判断漏失的方法通常是通过统计前期漏失地层的岩性、漏失工况及漏失通道分析原因^[6,7,8,9,10],也可以结合地层力学与物理性质判断漏层特性^[11,12,13] ...

2009

0.0

2007

0.0

2009

0.0

2009

0.0

1997

0.0

2016

0.0

2012

0.0

2019

0.0

... 然而,经典数学又不太适合用于分析、处理地质学中的这类模糊问题,因此应用模糊数学的方法定量分析、研究、处理地质学中的模糊信息,具有更大的优越性^[14] ...

0.0

... 模糊数学是用定量的方法去研究、处理模糊现象的数学分支^[15] ...

1987

0.0

... 隶属规律^[16],为了实现模糊的井漏地质风险转向定量化评价,对漏失井的漏失原因进行统计分析,结合统计规律确定地质元素与井漏风险性的隶属关系,建立相适应的风险评价标准,进而建立单井井漏地质风险元素矩阵 ...

2008

0.0

... 其基本原理为：在系统分析过程中,把复杂的问题依据问题的性质或需要分解为若干有序层次,然后再根据对客观现实的认识和判断,给出每一层次元素间相对重要性的定量表示,即所谓构造比较判断矩阵,再依据数学方法求出判断矩阵的最大特征根及其特征向量,依次确定每一层次内元素间的相对重要性次序的权值^{[17,18,19,20]} ...

2014

0.0

... 设井漏地质风险评价元素集合U={地层断裂深度a₁,地层曲率大小a₂,火山通道位置a₃,火成岩类型a₄,构造位置a₅,断裂系统a₆,断层倾角a₇,地层压力系数a₈},并对其各元素采用1~9标度法^[18,19]进行两两对比,尽可能减少性质不同元素相互比较的困难 ...

2011

0.0

... 依据层次分析表^[19]可知,随机一致性指标R_I值为1 ...

2017

0.0

2014

0.0

... 用1、3、5、7、9表示两元素之间相对重要程度,1、1/3、1/5、1/7、1/9表示两元素之间相对不重要程度,1表示同等重要,3表示稍微重要,5表示明显重要,7表示强烈重要,9表示极端重要,其中间值2、4、6、8表示重要性位于其前后两重要性之间^[21],据此建立比较判断矩阵M（公式1）得到归一化后特征向量#cod#x003c9 ...