基于六臂地层倾角资料的井眼扩大系数对录井迟到时间的校正

引用本文

徐长凯, 刘晓亮, 王俊. 基于六臂地层倾角资料的井眼扩大系数对录井迟到时间的校正[J]. 录井工程, 2023,34(2): 39-44.
XU Changkai, LIU Xiaoliang, WANG Jun. Correction of mud logging lag time by borehole enlargement coefficient based on six-arm dipmeter log[J]. Mud Logging Engineering, 2023,34(2): 39-44.
Doi:10.3969/j.issn.1672-9803.2023.02.007 复制到剪切板

Permissions

《录井工程》杂志社所有

基于六臂地层倾角资料的井眼扩大系数对录井迟到时间的校正

徐长凯, 刘晓亮, 王俊

中国石油大庆钻探工程公司地质录井一公司

作者简介：徐长凯工程师,1970年生,2014年毕业于东北石油大学石油工程专业,现在大庆钻探地质录井一公司资料采集二分公司从事综合录井管理工作。通信地址：163411 黑龙江省大庆市地质录井一公司资料采集二分公司。电话：（0459）5691861。E-mail：xuchangkai@petrochina.com.cn

收稿日期: 2023-04-09

摘要

伊拉克B油田的Sulaiy地层“糖葫芦串”形的椭圆井眼非常发育,对迟到时间影响较大。基于六臂地层倾角测井资料,采用最佳逼近的椭圆拟合井眼实际情况,并引入井眼扩大系数克服井径扩大率表征裸眼段井眼规则度方面的不足,解决了井眼不规则而引起的迟到时间不精准问题。在实际生产中,应用文中迟到时间校正公式对伊拉克B油田5口井迟到时间进行校正,使录井深度（迟到井深）与电测深度绝对误差降至1.4 m以内,满足了B油田生产需求,效果良好。

关键词: 迟到时间; Sulaiy地层; 椭圆井眼; 六臂地层倾角; 最佳逼近; 椭圆拟合; 井径扩大率; 井眼扩大系数

中图分类号:TE132.1 文献标志码:A

Correction of mud logging lag time by borehole enlargement coefficient based on six-arm dipmeter log

XU Changkai, LIU Xiaoliang, WANG Jun

No.1 Mud Logging Company of CNPC Daqing Drilling & Exploration Engineering Corporation, Daqing, Heilongjiang 163411, China

Abstract

The "sugarcoated haws on sticks string" shaped elliptical hole of Sulaiy Formation in Iraq B oilfiled is very developed and has a great impact on the lag time. Based on the six-arm dipmeter log, the best approximation ellipse is used to fit the actual situation of the borehole. And the introduction of borehole enlargement coefficient overcomes the shortcomings of hole enlargement ratio in characterizing the borehole regularity of the open hole interval, and solves the problem of inaccurate lag time caused by borehole irregularity. In actual production, the lag time correction formula in this paper was applied to correct the lag time of five wells in Iraq B oilfield, which can reduce the absolute error between mud logging depth （lag well depth） and electric depth to within 1.4 m, and meet the production demand of B oilfield with good results.

Keyword: lag time; Sulaiy Formation; elliptical hole; six-arm stratigraphic dip; best approximation; ellipse fitting; hole enlargement ratio; borehole enlargement coefficient

文章图片

0 引言

伊拉克B油田位于伊拉克南部与伊朗交界处, 构造上位于中东波斯湾盆地扎格罗斯山构造带西缘, 为轴向近似南北向的长轴背斜^[1]。该区域曾经历早白垩世被动大陆边缘与晚白垩世-新生代前陆盆地多期较强烈的南北向差异性构造活动与近东西向的挤压^[2]。受地质构造应力的剪切、拉伸作用以及钻头附近地应力释放等多重力学作用影响, Sulaiy地层“ 糖葫芦串” 形的椭圆井眼非常发育, 其椭圆长轴（最小水平主应力）发育方位几乎一致, 集中在144° ~324° , 椭圆短轴（最大水平主应力）方位集中在54° ~234° , 井眼受地质构造应力作用明显。在录井资料采集过程中, 鉴于椭圆井眼的发育程度对录井迟到时间的影响较明显, 本文基于六臂地层倾角测井资料, 采用拟合最佳逼近椭圆求解井眼扩大系数的方法, 对迟到时间理论公式进行修正, 使之更符合实际情况, 提高了录井资料采集精准度。

1 录井迟到时间理论计算公式

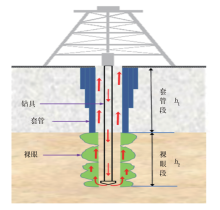
录井迟到时间是指在石油天然气钻井过程中, 钻井液携带岩屑与油气水, 沿着井筒与钻具所形成的环形空间从井底上返到井口取样位置所需的时间, 其精准度直接影响上返岩屑、油气水、钻井液及气测等多项资料的采集质量, 特别是在快速钻井条件下, 迟到时间不准确容易导致对储层及储层流体性质的误判^[3]。迟到时间理论计算公式如下：

$T_{迟} ＝ \frac{V_{1} + V_{2}}{Q} ＝ \frac{π ({d_{1}}^{2} - {d_{2}}^{2}) h_{1} + π (D^{2} - {d_{2}}^{2}) h_{2}}{4 Q}$ （1）

其中： $V_{1} ＝ \frac{1}{4} π ({d_{1}}^{2} - {d_{2}}^{2}) h_{1}$

$V_{2} ＝ \frac{1}{4} π (D^{2} - {d_{2}}^{2}) h_{2}$

式中： $T_{迟}$ 为迟到时间理论值, min; $V_{1}$ 为套管段环空体积, m³; $V_{2}$ 为裸眼段环空体积, m³; $Q$ 为钻井液泵总排量, m³/min; $D$ 为钻头直径, m; $d_{1}$ 为套管内径, m; $d_{2}$ 为钻具外径, m; $h_{1}$ 为套管下深, m; $h_{2}$ 为钻头在裸眼井段下深, m。

由录井迟到时间的理论计算公式可知：在钻井液泵总排量、钻头直径、钻具外径、钻头下深等参数一定时, 裸眼段环空体积是影响迟到时间精准度的最关键因素。在井筒形成过程中, 钻头周围应力场的改变会导致井壁失稳, 井眼通常呈现不规则形态（图1）, 而现场迟到时间的计算一般采用钻头尺寸代替井径, 忽略了裸眼段井眼空间规则与否的影响, 使得迟到时间理论计算值与实际情况误差较大, 且随着井深的增加, 误差会越来越大^[4]。因此, 利用井眼扩大系数量化裸眼井段井眼规则程度, 并对理论迟到时间进行校正, 可提高资料采集的精准度。

	Figure Option View Download New Window
	图1 井眼及环空示意

2 录井迟到时间的校正方法

2.1 六臂地层倾角测井原理简述

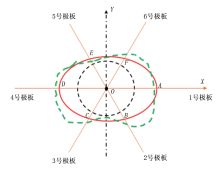
研究表明^{[5, 6, 7]}：力学原因引起的井眼坍塌最终形成椭圆井眼, 且椭圆面垂直于井眼轴线^[8], 其长轴远大于钻头直径, 短轴则接近钻头直径或者比钻头直径大的多^[9]。伊拉克B油田作业现场采用六臂地层倾角测井获取椭圆井眼的数据, 所用测井仪器具有6个彼此对称、互成60° 夹角的推靠臂^[10], 确保6个极板与井壁有可靠的接触, 以便获取更多的测井信息, 具有判定井眼几何形状的能力^[11], 对井眼的几何形状反映更为灵敏^[12]。6条极板测量的井径曲线分别为C₁、C₂、C₃、C₄、C₅、C₆, 3条相隔60° 的双井径曲线分别为C_1-4、C_2-5、C_3-6（图2）。测井仪器在测量过程中会随着提升而不断旋转, 当测遇崩落井段时, 一对测臂将嵌入椭圆井眼长轴方向的槽内, 使仪器不再随着提升而旋转^[13], 从而获得椭圆形井眼长轴所在的方位。当C_1-4为最大时, 长轴所在方位即为1号极板方位P₁AZ; 当C_2-5为最大时, 长轴所在方位P₁AZ+60° ; 当C_3-6为最大时, 长轴所在方位P₁AZ+120° 。

	Figure Option View Download New Window
	图2 6条可伸缩臂结构极板分布及井眼示意

2.2 求解最佳逼近井眼的拟合椭圆长轴与短轴

由于六臂地层倾角资料没有能代表椭圆井眼长短轴的垂直双井径曲线, 需要拟合一个最佳逼近的椭圆井眼轨迹^[14]。由于研究区的井型均为直井, 实际最大井底井斜均小于3° , 那么同一口井中不同井段所形成的椭圆井眼可认为是共中心点, 即：每个裸眼段椭圆井眼的中心点均位于钻具正中心。椭圆井眼轨迹拟合具体步骤如下。

2.2.1 建立标准拟合椭圆的参数方程

标准拟合椭圆的参数方程为：

$\{\begin{array}{l} x ＝ \frac{a}{2} \cos θ \\ y ＝ \frac{b}{2} \sin θ \end{array}$ （ $a > b > 0$ ）（2）

式中：θ 为椭圆上的任何一点与原点之间连线与X轴之间的夹角, （° ）; a为椭圆长轴; b为椭圆短轴; x、y分别为椭圆上横、纵坐标值。

2.2.2 建立直角坐标系求解椭圆长轴与短轴

当C_1-4最大时, 以井眼中心O为原点, C_1-4为X轴建立直角坐标系（图2）, 由椭圆的参数方程可知, 6条井径在拟合椭圆上的坐标分别为：

$A （ \frac{a}{2} \cos 0 ° ， \frac{b}{2} \sin 0 ° ）$ , $B （ \frac{a}{2} \cos 300 ° ， \frac{b}{2} \sin 300 ° ）$ , $C （ \frac{a}{2} \cos 240 ° ， \frac{b}{2} \sin 240 ° ）$ , $D （ \frac{a}{2} \cos 180 ° ， \frac{b}{2} \sin 180 ° ）$ , $E （ \frac{a}{2} \cos 120 ° ， \frac{b}{2} \sin 120 ° ）$ , $F （ \frac{a}{2} \cos 60 ° ， \frac{b}{2} \sin 60 ° ）$

其中, 令cos0° =K₁, sin0° =K₁′ , cos300° =K₂, sin300° =K₂′ , cos240° =K₃, sin240° =K₃′ , cos180° =K₄, sin180° =K₄′ , cos120° =K₅, sin120° =K₅′ , cos60° =K₆, sin60° =K₆′ 。

令$f(a,b)={{(\frac{a}{2}{{K}_{1}}-\frac{{{C}_{1}}}{2}{{K}_{1}})}^{2}}+{{(\frac{a}{2}{{K}_{2}}-\frac{{{C}_{2}}}{2}{{K}_{2}})}^{2}}+{{(\frac{a}{2}{{K}_{3}}-\frac{{{C}_{3}}}{2}{{K}_{3}})}^{2}}+{{(\frac{a}{2}{{K}_{4}}-\frac{{{C}_{4}}}{2}{{K}_{4}})}^{2}}+{{(\frac{a}{2}{{K}_{5}}-\frac{{{C}_{5}}}{2}{{K}_{5}})}^{2}}+{{(\frac{a}{2}{{K}_{6}}-\frac{{{C}_{6}}}{2}{{K}_{6}})}^{2}}+$ ${{(\frac{b}{2}{{K}_{1}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{1}}}{2}{{K}_{1}}\text{ }\!\!'\!\!\text{ })}^{2}}+{{(\frac{b}{2}{{K}_{2}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{2}}}{2}{{K}_{2}}\text{ }\!\!'\!\!\text{ })}^{2}}+{{(\frac{b}{2}{{K}_{3}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{3}}}{2}{{K}_{3}}\text{ }\!\!'\!\!\text{ })}^{2}}+{{(\frac{b}{2}{{K}_{4}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{4}}}{2}{{K}_{4}}\text{ }\!\!'\!\!\text{ })}^{2}}+{{(\frac{b}{2}{{K}_{5}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{5}}}{2}{{K}_{5}}\text{ }\!\!'\!\!\text{ })}^{2}}+{{(\frac{b}{2}{{K}_{6}}\text{ }\!\!'\!\!\text{ }-\frac{{{C}_{6}}}{2}{{K}_{6}}\text{ }\!\!'\!\!\text{ })}^{2}}$

当所拟合的椭圆最佳逼近实际井眼轨迹时, 则满足^{[14, 15]}：

$\{\begin{array}{l} \frac{\partial f (a, b)}{\partial a} ＝ 0 \\ \frac{\partial f (a, b)}{\partial b} ＝ 0 \end{array}$ （3）

对公式（3）偏导求解椭圆的长轴与短轴分别为：

$a ＝ \frac{C_{1} + C_{4}}{3} + \frac{C_{2} + C_{3} + C_{5} + C_{6}}{12}$

$b ＝ \frac{C_{2} + C_{3} + C_{5} + C_{6}}{4}$

同理, 当C_2-5最大时：

$a ＝ \frac{C_{2} + C_{5}}{3} + \frac{C_{1} + C_{3} + C_{4} + C_{6}}{12}$

$b = \frac{C_{1} + C_{3} + C_{4} + C_{6}}{4}$

当C_3-6最大时：

$a ＝ \frac{C_{3} + C_{6}}{3} + \frac{C_{1} + C_{2} + C_{4} + C_{5}}{12}$

$b ＝ \frac{C_{1} + C_{2} + C_{4} + C_{5}}{4}$

2.3 求解井眼扩大系数并修正迟到时间理论公式

椭圆井眼通常采用长轴a与钻头直径D表征井径扩大率（ $k$ ）^[8]：

$k ＝ \frac{a - D}{D} \times 100 %$ （4）

平均井径扩大率（ $\bar{k}$ ）：

$\bar{k}\text{=}\frac{1}{n}\underset{i=1}{\overset{n}{\mathop \sum }}\,{{k}_{i}}$（5）

校正后的裸眼段环空体积（ ${V_{2}}^{'}$ ）^[4]：

${V_{2}}^{'} ＝（ 1 + \bar{k} ） V_{2} ＝ \frac{1}{4} π （ 1 + \bar{k} ）（ D^{2} - {d_{2}}^{2} ） h_{2}$ （6）

采用平均井径扩大率校正后迟到时间（ $T_{迟}^{'}$ ）计算公式：

$T_{迟}^{'} ＝ \frac{V_{1} + {V_{2}}^{'}}{Q} ＝ \frac{π ({d_{1}}^{2} - {d_{2}}^{2}) h_{1} + π (1 + \bar{k}) (D^{2} - {d_{2}}^{2}) h_{2}}{4 Q}$ （7）

由于椭圆井眼不同位置处井径扩大率各不相同, 仅采用长轴以“ 以线带面” 的方式无法精准反映复杂井眼扩大情况, 利用井径扩大系数校正迟到时间的公式（7）在椭圆井眼中应用效果不佳。笔者采用裸眼段井眼面积与钻头面积关系表征井眼坍塌程度, 并定名为井眼扩大系数（ $μ$ ）, 即裸眼段井眼面积相对钻头面积的差值与钻头面积的比值：

$μ ＝ \frac{S_{井眼} - S_{钻头}}{S_{钻头}}$ （8）

式中： $μ$ 为井眼扩大系数, 无量纲; $S_{井眼}$ 为裸眼段井眼面积, m²; $S_{钻头}$ 为钻头面积, m²。

最佳逼近井眼的拟合椭圆接近实际井眼形状, 可近似认为：

$S_{井眼} ≅ S_{拟椭}$ （9）

式中： $S_{拟椭}$ 为拟合椭圆面积, m²。

由公式（8）、（9）得：

$\mu =\frac{{{S}_{拟椭}}-{{S}_{钻头}}}{{{S}_{钻头}}}=\frac{\text{ } \pi \text{ }(a/2)(b/2)-\text{ } \pi \text{ }{{(D/2)}^{2}}}{\text{ } \pi \text{ }{{(D/2)}^{2}}}=\frac{ab-{{D}^{2}}}{{{D}^{2}}}$（10）

统计并计算该区域椭圆井眼的平均井眼扩大系数（ $\overset{̅}{μ}$ ）：

$\bar{\mu }\text{=}\frac{1}{n}\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\mu }_{i}}$（11）

由公式（8）、（11）求解裸眼段平均井眼面积（ ${\bar{S}}_{井眼}$ ）：

${{\bar{S}}_{井眼}}=\left( 1+\bar{\mu } \right){{S}_{钻头}}$（12）

校正后的裸眼段环空体积：

${{V}_{2}}^{\prime\prime}=\left( {{{\bar{S}}}_{井眼}}-{{S}_{钻具}} \right){{h}_{2}}=\frac{\text{ } \pi \text{ }{{h}_{2}}\left[ \left( 1+\bar{\mu } \right){{D}^{2}}-{{d}_{2}}^{2} \right]}{4}$（13）

采用平均井眼扩大系数校正后的迟到时间 ${T″}_{迟校}$ 计算公式：

${{T}^{\prime\prime }}_{迟校}=\frac{\text{ } \pi \text{ }{{h}_{1}}{{d}_{1}}^{2}-{{d}_{2}}^{2}+\text{ }\pi \text{ }{{h}_{2}}\left[ 1+\bar{\mu }{{D}^{2}}-{{d}_{2}}^{2} \right]}{4Q}$（14）

3 应用效果

为了更加准确地反映施工区域地应力集中井段的椭圆井眼情况, 笔者选取了伊拉克B油田北部、中部、南部具有代表性的FH-12井等3口井的电测数据, 对采用上述方法计算的井眼扩大系数进行了统计分析（表1）, 井眼扩大系数区间为（0.207, 0.545）, 平均井眼扩大系数 $\overset{̅}{μ}$ 为0.461。

表1 采用本文方法计算的井眼扩大系数统计分析

以B油田Sulaiy地层为例（表2）：通过对比发现, 采用井眼扩大系数校正后迟到时间精准度更高, 录井深度与电测深度误差减少至1.4 m以内, 能够满足椭圆井眼条件下的资料采集工作。

表2 Sulaiy地层迟到时间理论计算公式与校正公式计算结果对比

4 结论

（1）在录井资料采集过程中, 由于无法实时跟踪椭圆井眼井径变化态势, 通常忽略井眼井径变化的影响, 直接采用迟到时间理论公式计算, 导致最终结果误差较大。

（2）伊拉克B油田Sulaiy地层发育“ 糖葫芦串” 形椭圆井眼, 可采用最佳逼近椭圆拟合井眼周轨迹以反映真实情况。在满足坐标差的平方和f（a, b）关于椭圆长轴（a）和短轴（b）的偏导数均为零的条件下, 利用六臂地层倾角测井资料可求解拟合椭圆的长轴与短轴。

（3）针对井径扩大率表征井眼存在“ 以线代面” 的不足, 本文引入井眼扩大系数。其采用裸眼段井眼面积相对钻头面积的差值与钻头面积的比值表征井眼坍塌程度, 在描述井眼方面更贴近实际情况。由于最佳逼近井眼的拟合椭圆接近实际井眼形状, 可使用拟合椭圆的面积代替实际井眼的面积以获取井眼扩大系数。

（4）通过对文中校正公式使用前、后对比验证：伊拉克B油田Sulaiy地层井眼平均扩大系数为0.461, 采用井眼扩大系数对迟到时间进行校正后录井深度与电测深度误差减少至1.4 m以内, 可满足本区域生产实践。

（编辑王丙寅）

参考文献

文献列表

[1]	付志方, 孙红军, 董立, 等. 差异构造演化控制倾斜油水界面之实例: 伊朗雅达油田[J]. 海相油气地质, 2017, 22(3): 67-72. FU Zhifang, SUN Hongjun, DONG Li, et al. Control effects on the tilted oil-water contact caused by differential structural evolution: A case of Yada Oilfield, Iran[J]. Marine Origin Petroleum Geology, 2017, 22(3): 67-72. [本文引用:1]
[2]	杜洋, 衣英杰, 辛军, 等. 伊朗SA油田Sarvak油藏大幅度倾斜油水界面成因探讨[J]. 石油实验地质, 2015, 37(2): 187-193. DU Yang, YI Yingjie, XIN Jun, et al. Genesis of large-amplitude tilting oil-water contact in Sarvak Formation in South Azadegan Oilfield, Iran[J]. Petroleum Geology & Experiment, 2015, 37(2): 187-193. [本文引用:1]
[3]	张建斌, 苑仁国. 迟到时间对储集层流体性质评价的影响分析与对策[J]. 录井工程, 2020, 31(1): 42-45, 51. ZHANG Jianbin, YUAN Renguo. Analysis and countermeasures of the impact of lag time on the evaluation of reservoir fluid properties[J]. Mud Logging Engineering, 2020, 31(1): 42-45, 51. [本文引用:1]
[4]	沈书锋, 郑玉朝, 李伟. 井径扩大率对岩屑迟到时间的影响校正[J]. 录井工程, 2009, 20(1): 61-62. SHEN Shufeng, ZHENG Yuchao, LI Wei. Correction of the effect of hole enlargement ratio on lag time of cuttings[J]. Mud Logging Engineering, 2009, 20(1): 61-62. [本文引用:2]
[5]	王金凤, 邓金根, 李宾. 井壁坍塌破坏过程的数值模拟及井径扩大率预测[J]. 石油钻探技术, 2000, 28(6): 13-14. WANG Jinfeng, DENG Jingen, LI Bin. Numerical simulation of borehole collapse procedure and prediction on well-hole enlargement[J]. Petroleum Drilling Techniques, 2000, 28(6): 13-14. [本文引用:1]
[6]	刘书杰, 周建良, 何保生, 等. 欠平衡钻井条件下的井径扩大率预测技术[J]. 中国海上油气, 2007, 19(5): 335-337. LIU Shujie, ZHOU Jianliang, HE Baosheng, et al. The prediction technology of hole enlargement ratio in the condition of underbalanced drilling[J]. China Offshore Oil and Gas, 2007, 19(5): 335-337. [本文引用:1]
[7]	李军, 陈勉, 张广清, 等. 易坍塌地层椭圆形井眼内套管应力的有限元分析[J]. 石油大学学报(自然科学版), 2004, 28(2): 45-48. LI Jun, CHEN Mian, ZHANG Guangqing, et al. Analysis on stress distribution of casing in sloughing formation with finite element method[J]. Journal of China University of Petroleum(Edition of Natural Science), 2004, 28(2): 45-48. [本文引用:1]
[8]	赵凯, 韩继勇, 许永华. 定向井井径扩大率计算模型及影响因素分析[J]. 断块油气田, 2016, 23(5): 638-642. ZHAO Kai, HAN Jiyong, XU Yonghua. Borehole diameter enlargement ratio calculation model of directional wells and influence factors analysis[J]. Fault-Block Oil & Gas Field, 2016, 23(5): 638-642. [本文引用:2]
[9]	曲国胜, 张华, 叶洪. 黄骅坳陷井壁崩落法现代构造应力场测量[J]. 华北地震科学, 1993, 11(3): 9-18. QU Guosheng, ZHANG Hua, YE Hong. The principal stress orientations by the borehole breakouts in Huanghua Depression[J]. North China Earthquake Sciences, 1993, 11(3): 9-18. [本文引用:1]
[10]	高兴军, 付鑫生, 于兴河, 等. 六臂地层倾角处理中的球面映像技术分析[J]. 石油地球物理勘探, 2002, 37(2): 129-133. GAO Xingjun, FU Xinsheng, YU Xinghe, et al. Analysis of spherical projection technology in six-arm dipmeter processing[J]. Oil Geophysical Prospecting, 2002, 37(2): 129-133. [本文引用:1]
[11]	张志伟. 地层倾角测井资料在海拉尔盆地乌尔逊油田的应用[J]. 国外测井技术, 2010(175): 34-36. ZHANG Zhiwei. Application of diplog data in Wuerxun Oilfield, Hailar Basin[J]. World Well Logging Technology, 2010(175): 34-36. [本文引用:1]
[12]	程希, 许杰, 王骏, 等. 六臂地层倾角测井仪功能电路及液压测试器实现[J]. 石油管材与仪器, 2015, 1(1): 84-86. CHENG Xi, XU Jie, WANG Jun, et al. Design of the logging function circuits and hydraulic test device of six arm dipmeter[J]. Petroleum Tubular Goods & Instruments, 2015, 1(1): 84-86. [本文引用:1]
[13]	印兴耀, 马妮, 马正乾. 地应力预测技术的研究现状与进展[J]. 石油物探, 2018, 57(4): 488-504. YIN Xingyao, MA Ni, MA Zhengqian, et al. Review of in-situ stress prediction technology[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 488-504. [本文引用:1]
[14]	魏阳庆, 刘峰, 孙彩云. 利用六臂地层倾角测井资料分析地应力[J]. 断块油气田, 2005, 12(5): 78-80. WEI Yangqing, LIU Feng, SUN Caiyun. Using six-arm dipmeter log to analyze ground stress[J]. Fault-Block Oil & Gas Field, 2005, 12(5): 78-80. [本文引用:2]
[15]	李岳生, 黄友谦. 数值逼近[M]. 北京: 人民教育出版社, 1978. LI Yuesheng, HUANG Youqian. Numerical approximation[M]. Beijing: People＇s Education Press, 1978. [本文引用:1]

2017

0.0

... 0 引言伊拉克B油田位于伊拉克南部与伊朗交界处,构造上位于中东波斯湾盆地扎格罗斯山构造带西缘,为轴向近似南北向的长轴背斜^[1] ...

2015

0.0

... 该区域曾经历早白垩世被动大陆边缘与晚白垩世-新生代前陆盆地多期较强烈的南北向差异性构造活动与近东西向的挤压^[2] ...

2020

0.0

... 1 录井迟到时间理论计算公式录井迟到时间是指在石油天然气钻井过程中,钻井液携带岩屑与油气水,沿着井筒与钻具所形成的环形空间从井底上返到井口取样位置所需的时间,其精准度直接影响上返岩屑、油气水、钻井液及气测等多项资料的采集质量,特别是在快速钻井条件下,迟到时间不准确容易导致对储层及储层流体性质的误判^[3] ...

2009

0.0

... 在井筒形成过程中,钻头周围应力场的改变会导致井壁失稳,井眼通常呈现不规则形态（图1）,而现场迟到时间的计算一般采用钻头尺寸代替井径,忽略了裸眼段井眼空间规则与否的影响,使得迟到时间理论计算值与实际情况误差较大,且随着井深的增加,误差会越来越大^[4] ...

... 校正后的裸眼段环空体积（ V2'）^[4]： ...

2000

0.0

... 1 六臂地层倾角测井原理简述研究表明^[5,6,7]：力学原因引起的井眼坍塌最终形成椭圆井眼,且椭圆面垂直于井眼轴线^[8],其长轴远大于钻头直径,短轴则接近钻头直径或者比钻头直径大的多^[9] ...

2007

0.0

2004

0.0

2016

0.0

... 3 求解井眼扩大系数并修正迟到时间理论公式椭圆井眼通常采用长轴a与钻头直径D表征井径扩大率（ k）^[8]： ...

1993

0.0

2002

0.0

... 夹角的推靠臂^[10],确保6个极板与井壁有可靠的接触,以便获取更多的测井信息,具有判定井眼几何形状的能力^[11],对井眼的几何形状反映更为灵敏^[12] ...

2010

0.0

2015

0.0

2018

0.0

... 测井仪器在测量过程中会随着提升而不断旋转,当测遇崩落井段时,一对测臂将嵌入椭圆井眼长轴方向的槽内,使仪器不再随着提升而旋转^[13],从而获得椭圆形井眼长轴所在的方位 ...

2005

0.0

... 2 求解最佳逼近井眼的拟合椭圆长轴与短轴由于六臂地层倾角资料没有能代表椭圆井眼长短轴的垂直双井径曲线,需要拟合一个最佳逼近的椭圆井眼轨迹^[14] ...

... 当所拟合的椭圆最佳逼近实际井眼轨迹时,则满足^[14,15]： ...

1978

0.0

... 当所拟合的椭圆最佳逼近实际井眼轨迹时,则满足^[14,15]： ...