基于录井参数不确定性的随钻地层压力分析预测

引用本文

徐婕, 姜维寨, 牛华夏, 杨学辛, 戴广阔, 杨清纯. 基于录井参数不确定性的随钻地层压力分析预测[J]. 录井工程, 2023,34(3): 7-14.
XU Jie, JIANG Weizhai, NIU Huaxia, YANG Xuexin, DAI Guangkuo, YANG Qingchun. Analysis and prediction of formation pressure while drilling based on uncertainties of mud logging parameters[J]. Mud Logging Engineering, 2023,34(3): 7-14.
Doi:10.3969/j.issn.1672-9803.2023.03.002 复制到剪切板

Permissions

《录井工程》杂志社所有

基于录井参数不确定性的随钻地层压力分析预测

徐婕, 姜维寨, 牛华夏, 杨学辛, 戴广阔, 杨清纯

中国石油渤海钻探第二录井公司

作者简介：徐婕工程师,1988 年生,2010 年毕业于长江大学资源勘查专业,现在中国石油渤海钻探第二录井公司从事工程地质一体化工作。通信地址：062552 河北省任丘市渤海钻探第二录井公司地质研究评价中心。电话：（0317）270427。E-mail：xu_jie@cnpc.com.cn

收稿日期: 2023-04-25

基金: 中国石油渤海钻探工程公司揭榜挂帅重大研发项目“油气井工程地质一体化深度融合系统开发”（编号：2022ZD01F）

摘要

在同一岩性地层中,由于钻速、转盘转速、钻压、钻井液密度和岩石密度等录井参数存在不确定性,导致基于录井参数的随钻地层压力预测存在一定的不确定性。针对该问题,分析了钻速、转盘转速、钻压、钻井液密度和岩石密度等录井参数的不确定性特征,进而采用改进的Rosenbluthe方法推导得出 dc指数、上覆地层垂向应力及随钻地层压力的不确定性分析表达式,同时提出了基于录井参数的随钻地层压力不确定性分析方法,最后得到了地层压力的概率分布。以某区块HT 101井为例,分别应用不确定性分析方法和蒙特卡罗方法对地层压力的概率分布进行预测,结果表明,不确定性分析方法与蒙特卡罗方法的压力预测一致性达95%以上,其压力预测精度能够满足工程需要。

关键词: 随钻地层压力; 录井参数; 不确定性; Rosenbluthe方法; 概率分布; 蒙特卡罗方法

中图分类号:TE132.1 文献标志码:A

Analysis and prediction of formation pressure while drilling based on uncertainties of mud logging parameters

XU Jie, JIANG Weizhai, NIU Huaxia, YANG Xuexin, DAI Guangkuo, YANG Qingchun

No.2 Mud Logging Company, BHDC, CNPC, Renqiu, Hebei 062552, China

Abstract

In the strata of the same lithology, due to the uncertainties of mud logging parameters such as drilling speed, rotary speed, weight on bit, drilling fluid density and rock density, some uncertainties exist in predicting formation pressure while drilling based on mud logging parameters.To solve this problem, the uncertainty characteristics of mud logging parameters including drilling speed, rotary speed, weight on bit, drilling fluid density and rock density were analyzed. Then, the analytical expressions of uncertainties in dc index, vertical stress of overlying strata and formation pressure while drilling were derived by using the improved Rosenbluthe method. At the same time, a method for analyzing the uncertainties of formation pressure while drilling based on mud logging parameters was proposed, and the probability distribution of formation pressure was finally obtained. Taking well HT 101 in a block as an example, uncertainty analysis method and Monte Carlo method were used to predict the probability distribution of formation pressure respectively. The results showed that the consistency of pressure prediction between uncertainty analysis method and Monte Carlo method was more than 95%, and the accuracy of pressure prediction can meet the engineering needs.

Keyword: formation pressure while drilling; mud logging parameter; uncertainty; Rosenbluthe method; probability distribution; Monte Carlo method

文章图片

0 引言

地层压力是指地层中流体所承受的压力^{[1, 2]}, 其对于维持钻井过程中的井壁稳定性具有重要作用^{[3, 4]}。地层压力预测尤其是随钻地层压力预测一直是钻井工程的核心问题, 目前随钻地层压力预测中大多应用录井数据^[5], 然而即使对于同一地层, 钻速、转盘转速、钻压、钻井液密度、岩石密度等录井数据均存在一定的不确定性, 这导致基于上述参数计算得出的dc指数和上覆地层垂向应力存在不确定性, 进而使得随钻地层压力预测存在不确定性, 其预测结果也不是确切数值, 而是一个概率分布区间。因此, 通过对随钻地层压力进行不确定性分析, 获取地层压力的概率分布区间, 对实际钻井工程施工具有重要指导作用。

目前, 通过录井参数和dc指数建立随钻地层压力确定性模型已取得进展：Hottman和Johnson通过建立确定性模型预测随钻地层压力^[6]; Penebaker利用地震资料确定性预测随钻地层压力, 并确认准确获取层速度是用地震资料预测地层压力的关键; Eaton总结前人研究成果, 提出了基于电阻率、声波时差和dc指数的随钻地层压力关系式, 即伊顿法^[7]; Fillippone提出一个不依赖于正常压实趋势线, 而是利用层速度来预测地层压力的经验模型^[8]; 刘震等对Fillippone确定性模型进行了修正, 提高了地层压力预测精度^[9]。

此外, 部分学者引入不确定性分析方法预测地层压力：胜亚楠等^{[10, 11]}结合蒙特卡罗法模拟和概率分布理论, 建立了含可信度的地层压力求取方法, 得到了地层压力和钻井液密度的概率分布; 李莹莹^[12]通过处理已钻地层地震或测井资料, 利用概率统计理论对地层压力进行了不确定性分析, 定量描述含可信度区间的地层压力纵向剖面; 于浩^[13]使用基于机器学习的多变量地层压力预测方法获取多组预测地层压力并使用多组模拟对预测压力不确定性进行量化分析; 黄熠等^[14]分析了地层压力的不确定性, 并基于不确定度分析理论对钻井液密度的不确定性进行了概率分布分析; 魏凯等^[15]通过录井参数不确定性的概率分布和不确定度两种描述方法, 建立地质参数不确定性分析方法, 确定钻井地质参数的概率分布函数。

虽然前人在地层压力预测方面已取得很多研究成果, 但仍然存在以下不足：一是由于地层压力的不确定性, 预测的结果应该是一个区间, 而非一个固定的数值, 所以确定性模型很难对地层压力进行精确评价; 二是虽然已开展了地层压力的不确定性分析, 但是几乎所有的不确定性分析都是基于蒙特卡罗法, 而蒙特卡罗法计算效率较低, 制约了该方法在实际工程中的应用。针对上述问题, 本文通过引入改进的Rosenbluthe不确定性方法建立了基于录井参数的随钻地层压力预测模型, 获取地层压力的概率分布, 并与蒙特卡罗法对比验证其准确性。

1 录井参数不确定性分析

在同一岩性地层中, 钻速、转盘转速、钻压、钻井液密度、岩石密度等录井参数都存在一定的不确定性, 这导致同一地层各深度处的随钻地层压力预测存在不确定性。本文以某区块HT 101井5 010~6 357 m井段的录井资料为例, 分别对其钻速、转盘转速、钻压、钻井液密度及岩石密度等录井参数的不确定性数学特征进行统计。

1.1 钻速不确定性分析

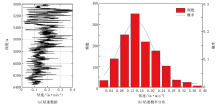
由图1a可知, HT 101井5 010~6 357 m井段的钻速在0~0.4 m/min范围内, 通过统计每0.04 m/min区间内的钻速数据个数, 拟合出钻速概率分布如图1b所示, 钻速具有不确定性, 其分布形式基本上满足正态分布。

	Figure Option View Download New Window
	图1 HT 101井钻速不确定性分析

1.2 转盘转速不确定性分析

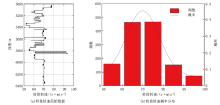
由图2a可知, HT 101井5 010~6 357 m井段的转盘转速在50~100 r/min范围内, 通过统计每10 r/min区间内的转盘转速数据个数, 拟合出转盘转速概率分

布如图2b所示, 转盘转速具有不确定性, 其分布形式基本上满足正态分布。

	Figure Option View Download New Window
	图2 HT 101井转盘转速不确定性分析

1.3 其他录井参数不确定性分析

同理, 采用上述分析方法对HT 101井5 010~6 357 m井段钻压、钻井液密度、岩石密度等其他录井参数进行了不确定性分析, 结果表明上述录井参数同钻速、转盘转速一样, 均具有不确定性, 其分布形式基本上均满足正态分布。钻速、转盘转速、钻压、钻井液密度及岩石密度等录井参数作为随机变量, 其不确定性特征如表1所示。

表1 HT 101井5 010~6 357 m井段录井参数不确定性特征

2 改进的Rosenbluthe不确定性分析方法

Rosenbluthe于1985年提出了一种计算由不同随机变量X构成的函数Y的简便方法, 称为Rosenbluthe法^[16]。崔维成等^[17]针对Rosenbluthe法存在的计算数值奇异和计算精度不稳等问题进行了改进, 提出了改进的Rosenbluthe法, 其计算过程如下。

假设随机变量为X₁, X₂, …, X_n, 其均值和标准差分别为μ _X₁, μ _X₂, …, μ _Xn和σ _X₁, σ _X₂, …, σ _Xn, 由此计算各随机变量的函数值y^*、y_i⁺、y_i^-, 公式如下。

y^*=G（μ _X₁, …, μ _Xi, …, μ _Xn）（1）

y_i⁺=G（μ _X₁, …, μ _Xi+σ _Xi, …, μ _Xn）（2）

y_i^-=G（μ _X₁, …, μ _Xi-σ _Xi, …, μ _Xn）（3）

根据公式（2）和公式（3）可计算两个系数μ _i和σ _i, 公式如下。

$μ_{i} = \frac{{y_{i}}^{+} + {y_{i}}^{-}}{2}$ （4）

$σ_{i} = \frac{|{y_{i}}^{+} - {y_{i}}^{-}|}{2}$ （5）

通过以下公式可确定 ${y_{ij}}^{+}$ 和 ${y_{ij}}^{-}$ 的函数值：

y_ij⁺=G（μ _X₁, …, μ _Xi+σ _Xi, …, μ _Xj+σ _Xj, …, μ _Xn）（6）

y_ij^-=G（μ _X₁, …, μ _Xi-σ _Xi, …, μ _Xj-σ _Xj, …, μ _Xn）（7）

通过以下公式计算μ _ij、Δ μ _i、Δ μ _ij的函数值：

$μ_{ij} = \frac{{y_{ij}}^{+} + {y_{ij}}^{-}}{2}$ （其中i< j）（8）

Δ μ _i=μ _i-y^* （9）

Δ μ _ij=μ _ij-y^*-Δ μ _i-Δ μ _j （10）

最后, 将上述函数值代入公式（11）, 得到由不同随机变量X构成的函数Y的均值和标准差：

$\{\begin{array}{l} μ_{Y} = y^{*} + \sum_{i = 1}^{n} Δ μ_{i} \\ {σ_{Y}}^{2} = \sum_{i = 1}^{n} {σ_{i}}^{2} + 2 \sum_{i = 1}^{n} （ Δ μ_{i} ）^{2} + \sum_{i = 1, j = 1, i < j}^{n} （ Δ μ_{ij} ）^{2} \end{array}$ （11）

3 dc指数和上覆地层垂向应力不确定性分析

由于钻速、转盘转速、钻压等录井工程参数, 以及钻井液密度、岩石密度参数均为具有不确定性的随机变量, 导致基于录井参数得出的dc指数和上覆地层垂向应力也属于具有不确定性的随机变量。

3.1 dc指数不确定性分析

本文针对录井参数的不确定性, 采用改进的Rosenbluthe法推导得出了dc指数^[16]这一随机变量的不确定性分析表达式, 其均值和标准差公式如下：

$\{\begin{array}{l} μ_{dc} = \frac{\lg （ 0.0547 μ_{X 1} / μ_{X 2} ）}{\lg （ 0.06847 μ_{X 3} / D_{b} ）} \times \frac{G_{n}}{μ_{X 4}} + \sum_{i = 1}^{4} Δ μ_{i} \\ {σ_{dc}}^{2} = \sum_{i = 1}^{4} {σ_{i}}^{2} + 2 \sum_{i = 1}^{4} （ Δ μ_{i} ）^{2} + \sum_{i = 1, j = 1, i < j}^{4} （ Δ μ_{ij} ）^{2} \end{array}$ （12）

其中：

$Δ μ_{i} = \frac{{y_{i}}^{+} + {y_{i}}^{-}}{2} - \frac{\lg （ 0.0547 μ_{X 1} / μ_{X 2} ）}{\lg （ 0.06847 μ_{X 3} / D_{b} ）} \times \frac{G_{n}}{μ_{X 4}}$

$σ_{i} = \frac{|{y_{i}}^{+} - {y_{i}}^{-}|}{2}$

$Δ μ_{ij} = \frac{{y_{ij}}^{+} + {y_{ij}}^{-}}{2} - \frac{\lg （ 0.0547 μ_{X 1} / μ_{X 2} ）}{\lg （ 0.06847 μ_{X 3} / D_{b} ）} \times \frac{G_{n}}{μ_{X 4}} -$ $Δ μ_{i} - Δ μ_{j}$

式中：μ _dc为dc指数的均值, 无量纲; D_b为钻头直径, mm; G_n为静水压力梯度, MPa/m; μ _X₁为钻速的均值, m/min; μ _X₂为转盘转速的均值, r/min; μ _X₃为钻压的均值, kN; μ _X₄为钻井液密度的均值, g/cm³; σ _dc为dc指数的标准差, 无量纲; y_i⁺、y_i^-、y_ij⁺、y_ij^-（i, j=1、2、3、4, 且i< j）为函数值, 可由μ _X₁、σ _X₁、μ _X₂、σ _X₂、μ _X₃、σ _X₃、μ _X₄、σ _X₄代入公式（2）、（3）、（6）、（7）获得（σ _X₁为钻速的标准差, m/min; σ _X₂为转盘转速的标准差, r/min; σ _X₃为钻压的标准差, kN; σ _X₄为钻井液密度的标准差, g/cm³）。

3.2 上覆地层垂向应力不确定性分析

采用改进的Rosenbluthe法推导得出了上覆地层垂向应力^[17]这一随机变量的不确定性分析表达式, 其均值和标准差见公式（13）：

$\{\begin{array}{l} μ_{σ V} = \int_{0}^{H} ρ （ h ） g d h + Δ μ_{5} \\ {σ_{σ V}}^{2} = {σ_{5}}^{2} + 2 （ Δ μ_{5} ）^{2} \end{array}$ （13）

其中：

$Δ μ_{5} = \frac{{y_{5}}^{+} + {y_{5}}^{-}}{2} - \int_{0}^{H} ρ （ h ） g d h$

$σ_{5} = \frac{|{y_{5}}^{+} - {y_{5}}^{-}|}{2}$

式中：μ _σ_V为上覆地层垂向应力的均值, MPa; H为深度, m; σ _σ_V为上覆地层垂向应力的标准差, MPa; y₅⁺、y₅^-为函数值, 由μ _X5、σ _X5代入公式（2）、（3）获得（μ _X5为岩石密度的均值, g/cm³; σ _X5为岩石密度的标准差, g/cm³）。

4 随钻地层压力不确定性分析

针对dc指数和上覆地层垂向应力的不确定性, 基于Eaton法^[18]和改进的Rosenbluthe法推导得出了随钻地层压力的不确定性分析表达式, 其均值和标准差见公式（14）：

$\{\begin{array}{l} μ_{Pp} = μ_{X 6} - （ μ_{X 6} - p_{0} ） {(\frac{dcs}{μ_{X 7}})}^{N} + \sum_{i = 6, 7} Δ μ_{i} \\ {σ_{Pp}}^{2} = \sum_{i = 6, 7} {σ_{i}}^{2} + 2 {\sum_{i = 6, 7} （ Δ μ_{i} ）}^{2} + （ Δ μ_{67} ）^{2} \end{array}$ （14）

其中：

$Δ μ_{i} = \frac{{y_{i}}^{+} + {y_{i}}^{-}}{2} - μ_{X 6} + （ μ_{X 6} - p_{0} ） {(\frac{dcs}{μ_{X 7}})}^{N}$

$σ_{i} = \frac{|{y_{i}}^{+} - {y_{i}}^{-}|}{2}$

$Δ μ_{67} = \frac{{y_{67}}^{+} + {y_{67}}^{-}}{2} - μ_{X 6} + （ μ_{X 6} - p_{0} ） {(\frac{dcs}{μ_{X 7}})}^{N} -$

$Δ μ_{6} - Δ μ_{7}$

式中： $μ_{Pp}$ 为随钻地层压力的均值, MPa; μ _X₆为上覆地层垂向应力的均值, MPa; μ _X₇为dc指数的均值, 无量纲; p₀为静水压力, MPa; $σ_{Pp}$ 为随钻地层压力的标准差, MPa; dcs为正常压实趋势线上的dc指数, 无量纲; N为Eaton指数, 无量纲; y_i⁺、y_i^-、y₆₇⁺、y₆₇^-为函数值, 由μ _X₆、σ _X₆、μ _X₇、σ _X₇代入公式（2）、（3）、（6）、（7）获得（σ _X₆为上覆地层垂向应力的标准差, MPa; σ _X₇为dc指数的标准差, 无量纲）。

计算求得随钻地层压力的均值和标准差后, 再结合地层压力作为随机变量的最合理分布形式, 即可得到随钻地层压力的概率分布。

5 随钻地层压力测算应用分析

以HT 101井5 010~6 357 m井段为例, 进行基于录井参数不确定性的随钻地层压力测算应用分析, 并采用行业内公认的测算精度较高的蒙特卡罗法对dc指数和随钻地层压力进行不确定性分析所获得的预测结果来验证本文研究方法的精准度。

5.1 随钻地层压力的不确定性分析

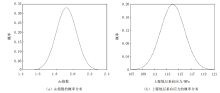
根据公式（1）-公式（13）和表1中的数据, 可以得到HT 101井5 010~6 357 m井段dc指数和上覆地层垂向应力的均值和标准差（表2）。由于表1中的随机变量满足正态分布, 由表1中的随机变量构成的dc指数和上覆地层垂向应力函数也满足正态分布。图3为HT 101井5 010~6 357 m井段dc指数和上覆地层垂向应力的概率分布。

表2 dc指数和上覆地层垂向应力的均值和标准差

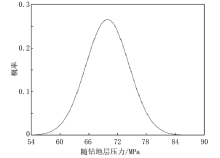
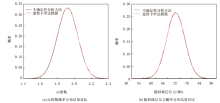
	Figure Option View Download New Window
	图3 HT 101井5 010~6 357 m井段dc指数和上覆地层垂向应力的概率分布

根据公式（14）和表2中的数据, 可以计算得到HT 101井5 010~6 357 m井段随钻地层压力的均值为69.78 MPa, 标准差为2.23 MPa。由于随钻地层压力公式中的随机变量dc指数和上覆地层垂向应力满足正态分布, 随钻地层压力也应满足正态分布, 其概率分布如图4所示。

	Figure Option View Download New Window
	图4 HT 101井5 010~6 357 m井段随钻地层压力的概率分布

5.2 不确定性分析方法精度验证

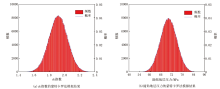
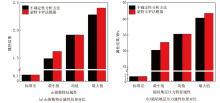
为了验证本文所研究方法的精度, 利用蒙特卡罗法^{[19, 20]}对HT 101井5 010~6 357 m井段dc指数和随钻地层压力进行了不确定性分析, 模拟次数为20万次, 得到了其dc指数和随钻地层压力的蒙特卡罗法模拟结果（图5）。将本文所研究的不确定性分析方法得到的dc指数和随钻地层压力概率分布曲线与蒙特卡罗法模拟得到的结果进行比较可知（图6）, 两种方法的概率分布曲线具有很高的一致性, 吻合程度超过95%。同时, 对两种方法得到的dc指数和随钻地层压力的最大值、最小值、均值、标准差等特征属性进行对比（图7）可知, dc指数和随钻地层压力的最大值、最小值、均值、标准差之间的差异非常小, 吻合程度高达98%。综合以上分析结果, 从概率分布曲线和随机变量特征属性的角度来看, 本文研究方法所得到的结果与蒙特卡罗法得到的结果非常接近, 可以满足实际工程需要。

	Figure Option View Download New Window
	图5 HT 101井5 010~6 357 m井段dc指数和随钻地层压力的蒙特卡罗法模拟结果

	Figure Option View Download New Window
	图6 两种方法得到的dc指数和随钻地层压力概率分布预测结果对比

	Figure Option View Download New Window
	图7 两种方法得到的dc指数和随钻地层压力特征属性结果对比

5.3 随钻地层压力测算结果分析

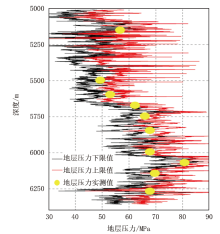
基于HT 101井的密度测井和声波测井曲线及表1数据, 并结合前文所提方法, 计算得出HT 101井5 010~6 357 m井段地层压力分布区间。图8为该井段地层压力分布区间和实测值对比。计算结果表明, 所有地层压力实测值均位于地层压力分布区间的中值线附近, 这在一定程度上验证了本文研究方法所测算得出的地层压力分布区间的合理性。以HT 101井5 704 m处的地层压力为例, 该深度处的地层压力分布区间为57.87~67.87 MPa, 分布区间中值为62.87 MPa, 地层压力实测值为59.15 MPa, 分布区间中值与实测值之间的误差仅为6.3%。另外, 其他深度处的地层压力分布区间中值和实测值误差也均低于10%, 表明本文所研究方法的计算精度可以满足现场要求。

	Figure Option View Download New Window
	图8 HT 101井5 010~6 357 m井段地层压力分布区间和实测值对比

6 结论

（1）针对钻速、转盘转速、钻压、钻井液密度、岩石密度不确定性以及由此引起的dc指数和上覆地层垂向应力不确定性对随钻地层压力的影响, 提出了基于改进的Rosenbluthe方法和Eaton法的随钻地层压力不确定性分析方法。

（2）建立了随钻地层压力不确定性分析的完整计算流程。首先统计钻速、转盘转速、钻压以及钻井液密度、岩石密度的不确定性特征; 然后由推导得出的dc指数和上覆地层垂向应力的不确定性表达式, 求出其均值和标准差; 最后将dc指数和上覆地层垂向应力的均值和标准差代入随钻地层压力的不确定性表达式, 得到地层压力的概率分布。

（3）将本文所研究的不确定性分析方法得到的dc指数和随钻地层压力的概率分布与蒙特卡罗法模拟结果进行了比较, 两者的吻合程度超过95%; 将不确定性分析方法所得到的地层压力与密度测井和声波测井曲线得到的结果进行比较, 误差均低于10%, 验证了本文所提方法的准确性。

（编辑唐艳军）

参考文献

文献列表

[1]	杨进, 刘书杰, 石磊, 等. 挤压构造地层压力预测模型研究[J]. 石油学报, 2009, 30(5): 764-768. YANG Jin, LIU Shujie, SHI Lei, et al. Research on prediction model for formation pressure in compression structure[J]. Acta Petrolei Sinica, 2009, 30(5): 764-768. [本文引用:1]
[2]	张晓广. 上覆岩层压力、地层压力和骨架应力的关系[J]. 科技创新与应用, 2018(12): 70-71. ZHANG Xiaoguang. Relationship between overlying rock pressure, formation pressure and skeleton stress[J]. Technology Innovation and Application, 2018(12): 70-71. [本文引用:1]
[3]	冯雪松, 魏安超, 任松涛, 等. 东方气田高温高压井完井技术难点及挑战[J]. 化学工程与装备, 2017(6): 104-106. FENG Xuesong, WEI Anchao, REN Songtao, et al. Technical difficulties and challenges of high temperature and high pressure well completion in Dongfang Gas Field[J]. Chemical Engineering & Equipment, 2017(6): 104-106. [本文引用:1]
[4]	方满宗, 刘和兴, 刘智勤, 等. 南海西部深水高温高压钻井液技术研究与应用[J]. 中国海上油气, 2017, 29(1): 89-94. FANG Manzong, LIU Hexing, LIU Zhiqin, et al. Research and application of deep water HTHP drilling fluid technology in western South China Sea[J]. China Offshore Oil and Gas, 2017, 29(1): 89-94. [本文引用:1]
[5]	刘春莹. 随钻测井地层压力预测技术研究[D]. 青岛: 中国石油大学(华东), 2014. LIU Chunying. Research on LWD formation pressure prediction technology[D]. Qingdao: China University of Petroleum(East China), 2014. [本文引用:1]
[6]	帕尔哈提, 雷德文, 邵雨. 准噶尔盆地复杂地区地层压力预测方法研究及应用[J]. 地球物理学进展, 2009, 24(4): 1377-1383. PA ErHati, LEI Dewen, SHAO Yu. Research and application of the formation pressure prediction method to complex regions in the Junggar Basin[J]. Progress in Geophysics, 2009, 24(4): 1377-1383. [本文引用:1]
[7]	艾池, 冯福平, 李洪伟. 地层压力预测技术现状及发展趋势[J]. 石油地质与工程, 2007, 21(6): 71-73, 76. AI Chi, FENG Fuping, LI Hongwei. Current status and development trend of formation pressure prediction technology[J]. Petroleum Geology & Engineering, 2007, 21(6): 71-73, 76. [本文引用:1]
[8]	常文会, 秦绪英. 地层压力预测技术[J]. 勘探地球物理进展, 2005, 28(5): 314-319. CHANG Wenhui, QIN Xuying. Formation pressure prediction technology[J]. Progress in Exploration Geophysics, 2005, 28(5): 314-319. [本文引用:1]
[9]	刘震, 张万选, 张厚福, 等. 辽西凹陷北洼下第三系异常地层压力分析[J]. 石油学报, 1993, 14(1): 14-24. LIU Zhen, ZHANG Wanxuan, ZHANG Houfu, et al. An analysis of abnormal formation pressures of Paleogene in the north sag of Liaoxi depression[J]. Acta Petrolei Sinica, 1993, 14(1): 14-24. [本文引用:1]
[10]	胜亚楠, 管志川, 赵廷峰, 等. 含可信度的地层压力求取方法研究[J]. 科学技术与工程, 2016, 16(2): 37-42. SHENG Ya'nan, GUAN Zhichuan, ZHAO Tingfeng, et al. Study on method of determining the formation pressure with credibility[J]. Science Technology and Engineering, 2016, 16(2): 37-42. [本文引用:1]
[11]	胜亚楠. 钻井工程风险评估与控制技术研究[D]. 青岛: 中国石油大学(华东), 2019. SHENG Ya'nan. Research on drilling engineering risk assessment and control technology[D]. Qingdao: China University of Petroleum(East China), 2019. [本文引用:1]
[12]	李莹莹. 基于地层信息不确定性的钻井设计风险评估方法研究[J]. 石化技术, 2021(6): 126-127. LI Yingying. Research on drilling design risk assessment method based on stratigraphic information uncertainty[J]. Petrochemical Industry Technology, 2021(6): 126-127. [本文引用:1]
[13]	于浩. 多变量孔隙压力预测与不确定性分析方法及应用研究[D]. 北京: 中国地质大学, 2020. YU Hao. Research on multivariate pore pressure prediction and uncertainty analysis method and its application[D]. Beijing: China University of Geosciences, 2020. [本文引用:1]
[14]	黄熠, 杨进, 胜亚楠, 等. 莺琼盆地高温高压钻井工程风险定量评价方法[J]. 中国海上油气, 2019, 31(4): 119-124. HUANG Yi, YANG Jin, SHENG Ya'nan, et al. Drilling engineering risk quantitative assessment for HTHP exploration wells in Yingqiong basin[J]. China Offshore Oil and Gas, 2019, 31(4): 119-124. [本文引用:1]
[15]	魏凯, 管志川, 马金山, 等. 钻井地质参数的不确定性表征及分析方法[J]. 中国石油大学学报(自然科学版), 2015, 39(5): 89-93. WEI Kai, GUAN Zhichuan, MA Jinshan, et al. Assessment method for uncertainty of geological parameters in well drilling[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2015, 39(5): 89-93. [本文引用:1]
[16]	王湘平. 随钻地层压力动态监测技术研究[D]. 北京: 中国地质大学, 2014. WANG Xiangping. Study on dynamic monitoring technology of formation pressure while drilling[D]. Beijing: China University of Geosciences, 2014. [本文引用:2]
[17]	崔维成, 徐向东, 邱强. 一种快速计算随机变量函数均值与标准差的方法[J]. 船舶力学, 1998, 2(6): 50-58. CUI Weicheng, XU Xiangdong, QIU Qiang. A fast method to calculate the mean and the stand ard deviation of the function of rand om variables[J]. Journal of Ship Mechanics, 1998, 2(6): 50-58. [本文引用:2]
[18]	EATON B A. Graphical method predicts geopressures worldwide[J]. World Oil, 1976, 183: 1: 51-56. [本文引用:1]
[19]	张锋, 徐建平, 胡玲妹, 等. PNN测井方法的蒙特卡罗模拟结果研究[J]. 地球物理学报, 2007, 50(6): 1924-1930. ZHANG Feng, XU Jianping, HU Lingmei, et al. Monte Carlo simulation result for the pulsed neutron -neutron logging method[J]. Chinese Journal of Geophysics, 2007, 50(6): 1924-1930. [本文引用:1]
[20]	胜亚楠, 管志川, 罗鸣, 等. 基于蒙特卡洛法的井壁稳定可靠度随机变量敏感性分析[J]. 石油钻采工艺, 2018, 40(1): 14-19. SHENG Ya'nan, GUAN Zhichuan, LUO Ming, et al. Sensitivity analysis of rand om variables for wellbore stability reliability based on Monte Carlo method[J]. Oil Drilling & Production Technology, 2018, 40(1): 14-19. [本文引用:1]

2009

0.0

... 0 引言地层压力是指地层中流体所承受的压力^[1,2],其对于维持钻井过程中的井壁稳定性具有重要作用^[3,4] ...

0.0

... 0 引言地层压力是指地层中流体所承受的压力^[1,2],其对于维持钻井过程中的井壁稳定性具有重要作用^[3,4] ...

0.0

... 0 引言地层压力是指地层中流体所承受的压力^[1,2],其对于维持钻井过程中的井壁稳定性具有重要作用^[3,4] ...

2017

0.0

... 0 引言地层压力是指地层中流体所承受的压力^[1,2],其对于维持钻井过程中的井壁稳定性具有重要作用^[3,4] ...

0.0

... 地层压力预测尤其是随钻地层压力预测一直是钻井工程的核心问题,目前随钻地层压力预测中大多应用录井数据^[5],然而即使对于同一地层,钻速、转盘转速、钻压、钻井液密度、岩石密度等录井数据均存在一定的不确定性,这导致基于上述参数计算得出的dc指数和上覆地层垂向应力存在不确定性,进而使得随钻地层压力预测存在不确定性,其预测结果也不是确切数值,而是一个概率分布区间 ...

2009

0.0

... 目前,通过录井参数和dc指数建立随钻地层压力确定性模型已取得进展：Hottman和Johnson通过建立确定性模型预测随钻地层压力^[6] ...

2007

0.0

... Eaton总结前人研究成果,提出了基于电阻率、声波时差和dc指数的随钻地层压力关系式,即伊顿法^[7] ...

2005

0.0

... Fillippone提出一个不依赖于正常压实趋势线,而是利用层速度来预测地层压力的经验模型^[8] ...

1993

0.0

... 刘震等对Fillippone确定性模型进行了修正,提高了地层压力预测精度^[9] ...

2016

0.0

... 此外,部分学者引入不确定性分析方法预测地层压力：胜亚楠等^[10,11]结合蒙特卡罗法模拟和概率分布理论,建立了含可信度的地层压力求取方法,得到了地层压力和钻井液密度的概率分布 ...

0.0

... 李莹莹^[12]通过处理已钻地层地震或测井资料,利用概率统计理论对地层压力进行了不确定性分析,定量描述含可信度区间的地层压力纵向剖面 ...

2020

0.0

... 于浩^[13]使用基于机器学习的多变量地层压力预测方法获取多组预测地层压力并使用多组模拟对预测压力不确定性进行量化分析 ...

2019

0.0

... 黄熠等^[14]分析了地层压力的不确定性,并基于不确定度分析理论对钻井液密度的不确定性进行了概率分布分析 ...

2015

0.0

... 魏凯等^[15]通过录井参数不确定性的概率分布和不确定度两种描述方法,建立地质参数不确定性分析方法,确定钻井地质参数的概率分布函数 ...

2014

0.0

... 2 改进的Rosenbluthe不确定性分析方法Rosenbluthe于1985年提出了一种计算由不同随机变量X构成的函数Y的简便方法,称为Rosenbluthe法^[16] ...

... 1 dc指数不确定性分析本文针对录井参数的不确定性,采用改进的Rosenbluthe法推导得出了dc指数^[16]这一随机变量的不确定性分析表达式,其均值和标准差公式如下： ...

1998

0.0

... 崔维成等^[17]针对Rosenbluthe法存在的计算数值奇异和计算精度不稳等问题进行了改进,提出了改进的Rosenbluthe法,其计算过程如下 ...

... 2 上覆地层垂向应力不确定性分析采用改进的Rosenbluthe法推导得出了上覆地层垂向应力^[17]这一随机变量的不确定性分析表达式,其均值和标准差见公式（13）： ...

1976

0.0

... 4 随钻地层压力不确定性分析针对dc指数和上覆地层垂向应力的不确定性,基于Eaton法^[18]和改进的Rosenbluthe法推导得出了随钻地层压力的不确定性分析表达式,其均值和标准差见公式（14）： ...

2007

0.0

... 2 不确定性分析方法精度验证为了验证本文所研究方法的精度,利用蒙特卡罗法^[19,20]对HT 101井5 010~6 357 m井段dc指数和随钻地层压力进行了不确定性分析,模拟次数为20万次,得到了其dc指数和随钻地层压力的蒙特卡罗法模拟结果（图5） ...

2018

0.0