引用本文
白倩, 赵军龙, 黄千玲, 许鉴源. H油田侏罗系延9储层物性参数预测方法研究[J]. 录井工程, 2023,34(3): 81-88.
BAI Qian, ZHAO Junlong, HUANG Qianling, XU Jianyuan. Study on prediction method of physical properties of Jurassic Yan 9 reservoir in H Oilfield[J]. Mud Logging Engineering, 2023,34(3): 81-88.
Doi:10.3969/j.issn.1672-9803.2023.03.013  
Permissions
Copyright©2023, 《录井工程》杂志社
《录井工程》杂志社 所有
H油田侏罗系延9储层物性参数预测方法研究
白倩①,②, 赵军龙①,②, 黄千玲①,②, 许鉴源①,②
①西安石油大学地球科学与工程学院
②西安石油大学陕西省油气成藏地质学重点实验室
通信作者：赵军龙 博士,教授,硕士生导师,1970 年生,主要从事测井资料处理与解释、复杂油气藏测井评价工作。通信地址：710065 陕西省西安市电子二路东段18 号西安石油大学。电话：18809186671。E-mail：zjl1970@163.com

作者简介：白倩 1998 年生,西安石油大学在读硕士研究生,研究方向为测井地质综合研究、测井资料处理与解释。通信地址：710065 陕西省西安市电子二路东段18 号西安石油大学。电话：15389439731。E-mail：2248027585@qq.com。

收稿日期: 2023-07-21
基金: 陕西省自然科学基础研究计划（编号：2019JM-359）
摘要

孔隙度和渗透率是描述储层物性特征的重要参数。常规的孔隙度和渗透率计算方法基于线性拟合,模型较单一且准确度不足。因此,基于文献调研和鄂尔多斯盆地H油田延9储层概况,总结了一些常用的孔隙度和渗透率计算方法,进而提出一种梯度提升决策树预测储层物性的方法,该方法将得到的物性参数和多条相关测井曲线作为梯度提升决策树的多元输入信息,通过训练得到预测孔隙度和渗透率的模型。H油田的21口井中6口井有实验数据,利用其中4口井与用常规的统计回归法和孔渗拟合法得出的15口井的物性数据进行训练,另外2口井作为测试集,结果表明梯度提升决策树储层预测方法的孔隙度、渗透率结果与岩心分析结果相关性均为0.9,常规方法计算结果的相关性也较高,分别为0.88、0.87。为提高模型解释精度,将常规方法计算的物性和训练集的物性及其测井曲线作为梯度提升决策树的多元输入信息进行训练,优化后梯度提升树结果与岩心分析结果相关性达到0.93。

关键词: 梯度提升决策树; 孔隙度; 渗透率; 储层物性
中图分类号:TE132.1 文献标志码:A
Study on prediction method of physical properties of Jurassic Yan 9 reservoir in H Oilfield
BAI Qian①,②, ZHAO Junlong①,②, HUANG Qianling①,②, XU Jianyuan①,②
①School of Earth Sciences and Engineering,Xi'an Shiyou University, Xi'an, Shaanxi 710065,China
②Shaanxi Key Laboratory of Petroleum Accumulation Geology,Xi'an Shiyou University,Xi'an, Shaanxi 710065,China
Abstract

Porosity and permeability are important parameters to describe reservoir physical properties. Conventional calculation methods of porosity and permeability are based on linear fitting, and the model is single and the accuracy is insufficient. Therefore, based on the literature investigation and the general situation of Yan 9 reservoir in Ordos Basin, this paper summarizes some commonly used calculation methods of porosity and permeability, and then puts forward a method of predicting reservoir physical properties by gradient boosting decision tree. In this method, the physical properties and many related logging curves are used as multivariate input information of gradient boosting decision tree, and the models for predicting porosity and permeability are obtained through training. There are 21 wells in H Oilfield, among which 6 wells have experimental data, 4 wells are trained with the physical property data of 15 wells obtained by conventional statistical regression method and porosity -permeability fitting method and the other 2 wells are taken as test sets. The results show that the correlation coeffieient between porosity and permeability results of gradient boosting decision tree reservoir prediction method and core analysis results is 0.9, and the correlation coefficients calculated by conventional methods are also high, which are 0.88 and 0.87 respectively. In order to improve the interpretation accuracy of the model, the physical properties calculated by conventional methods, the physical properties of training sets and their logging curves are trained as multivariate input information of gradient boosting decision tree, and the correlation coefficient between the optimized gradient boosting decision tree results and core analysis results reaches 0.93.

Keyword: gradient boosting tree decision; porosity; permeability; reservoir physical property
0 引言

储层物性的研究对于油气田的开发至关重要, 孔隙度和渗透率则是重要储层物性参数。提高孔隙度和渗透率的预测精度可以更准确地了解储层的状况, 有利于开发工作者根据储层状态进行开发。直接对岩心进行分析是准确得到储层孔隙度和渗透率的最直接方法, 但该方法取样成本高, 分析过程复杂且速度慢, 不适合大规模使用。传统的储层物性参数计算方法中, 使用测井数据计算储层物性的技术已经发展成熟, 为石油开采提供了坚实的基础。

随着计算机技术的不断发展, 计算储层物性的方法也变得多样化。在进行孔隙度预测时, 前人使用中子-密度交会、岩石物理线性模型迭代反演、结合岩心测试数据和测井数据建立模型、基于半监督聚类算法建立孔隙度预测模型对储层孔隙度进行预测[1, 2, 3, 4]; 通过预测成岩指数变化定量计算孔隙度[5, 6]; 基于地震测试资料、成像测井数据和人工智能技术也可以建立孔隙度预测模型[6, 7]。在进行渗透率预测时, 通过孔隙度与渗透率数据拟合法、数理统计方法可以建立渗透率模型, 采用核磁共振T2模型、孔喉结构参数结合核磁T2谱相定量计算渗透率, 用分形理论与渗流规律对渗透率进行研究[7, 8, 9, 10, 11, 12]。此外人工智能算法中的BP、GBDT、PSO-XGBoost和RBF等神经网络技术也可以用于预测储层物性[13, 14, 15, 16]。

本文以H油田B井区侏罗系延9储层为研究对象, 基于测井资料预测目标储层的物性参数。由于印支运动导致盆地发生了复杂的形变和剥削作用, 控制后期延9储层沉积, 在该研究区进行储层物性参数预测的新方法探索显得非常必要。因此, 基于文献调研和研究区概况, 总结了一些常用的孔隙度和渗透率计算方法, 并提出了一种梯度提升决策树预测储层物性的方法, 将其用于研究区的物性参数预测, 有助于提高预测准确性, 优化开发策略, 并利于最大程度地实现油藏资源的有效开采。

1 区域背景研究
1.1 地质概况

H油田位于甘肃省庆阳市, 坐落于庆西古河两岸的古地貌上。该地区构造位于鄂尔多斯盆地西南部、子午岭西北斜坡和演武北斜坡的局部隆起之上。在三叠纪末期, 印支运动导致华北地块西部的鄂尔多斯盆地迅速抬升和剥削变形, 对研究区目的层的沉积产生了明显的控制作用。此外, 目的层段顶部发育2~3套煤层, 其中部煤层最为发育, 导致油藏构造复杂。燕山运动区域东升, 形成了伊陕斜坡, 进一步在西倾单斜背景上构成了序列圈闭。甘陕、庆西与庆合三大古河相连, 形成了三叠系油气向上运移的通道, 使得部署区发育了物性较好的延9储层。延9储层的顶部构造为由西倾单斜背景上的差异压实作用形成的一系列低幅鼻状隆起, 其轴线近似东西向, 从下到上幅度逐渐变缓, 相应的圈闭面积也逐层减小。延9储层主要受到构造控制, 但岩性在局部地区对油层分布有一定的影响, 形成了以构造为主、岩性为辅的油藏。

1.2 储层基本特征

通过对研究区的扫描电镜、砂岩薄片鉴定等资料进行分析, 发现延9储层主要由灰-褐灰色细粒岩屑石英砂岩和石英岩屑砂岩组成。延9储层的面孔率一般在5%~14%之间, 平均为8.95%。孔隙类型主要包括粒间孔、溶孔和晶间孔, 储层的孔隙度平均值为18%, 并且大部分在10%~25%之间（图1a）。渗透率的平均值为9.8 mD, 主要分布在3~15 mD（图1b）范围内。据此可以判断延9储层属于中孔隙度、低渗透率储层, 储层物性较好。

图1 H油田延9储层物性分布

2 常规储层物性参数预测方法
2.1 孔隙度预测方法

孔隙度是描述储层相对容量的重要参数, 表示岩石中孔隙体积与总体积之间的比例。孔隙度的大小对于油藏勘探具有重要影响。在研究区内, 延9砂岩储层的孔隙度均值为18%, 属于中孔储层。

通过对砂岩储层孔隙度预测方法进行分类归纳, 系统分析了各种方法的计算原理及适用条件（表1）。岩石体积物理模型法、参数交会图法以及统计回归法是比较常用且相对容易实现的孔隙度计算方法; 通过分析核磁共振测井资料和地震资料的特征, 并结合相关的地质知识可以对孔隙度进行计算[17]; 根据储层特征和数据情况, 机器学习法提供了多种算法选择, 用于预测不同储层的孔隙度。

表1 储层常规孔隙度预测方法（据文献整理总结）
2.2 渗透率预测方法

渗透率是指在地层间压力差作用下, 岩石中通过石油和天然气的能力。研究区延9储层渗透率均值为9.8 mD, 分布在3~15 mD范围内, 属于低渗储层。

表2是据调研文献的储层常规渗透率预测方法, 其中孔渗拟合法简单且常用; Timur公式法和Herron模型不需要岩心测试数据[18]; 基于毛管压力资料, 常见的渗透率预测模型包括Winland模型、Klinkenberg模型、Purcell模型、Thomeer模型等[19, 20]; 核磁共振测井法常用的渗透率预测模型有SDR模型、Coates模型、Timur/Coates模型[21, 22]; 地层因素法、斯通利波（Stoneley）法也可反映储层渗透率[23]; 机器学习法也常被用于砂岩储层渗透率的预测。

表2 储层常规渗透率预测方法（据文献整理总结）
3 基于GBDT的储层物性参数预测研究

随着油气勘探开发的深入, 传统的基于线性假设的储层参数预测方法已无法满足对储层特征进行精细描述的需求。为了提高储层参数预测的准确度, 尝试利用多维度的测井数据和岩心分析结果, 建立非线性数学模型。

3.1 梯度提升决策树的预测原理

梯度提升决策树（GBDT）是一种基于决策树的集成学习算法。其中, 它的基学习器采用了分类回归树（CART）, 主要使用CART中的回归树进行训练。决策树通常被分为回归树和分类树两种类型, 而在GBDT中, 我们使用回归树来计算实际值, 以预测储层物性参数。

GBDT的核心思想在于, 每棵树的学习都是基于之前所有树结论和的残差信息。这个残差可以被视为一个累加量, 通过加上预测值能够得到真实值。因此, 每棵新树的学习就是为了减少之前所有树的预测结果与真实值之间的误差, 从而提高整个模型的预测精度。

梯度提升决策树学习算法包含的步骤如下[24]：

（1）构建初始化模型：

F0（x）=argminθ∑i=1NL（yi, θ）

式中： F0（x）为初始模型; argmin为一个优化操作符, 表示找到使得后面的目标函数取得最小值的参数θ ; θ 为模型参数; N为训练样本数量; L为损失函数; yi为第i个训练样本的真实标签。

（2）计算残差（负梯度）：

γim=-∂L（yi, F（xi））∂F（xi）F（xi）=Fm-1（xi）

式中： γim为第m轮迭代中第i个样本的残差; Fm-1（xi）为前m-1轮迭代后的模型对样本 xi的预测值。

（3）拟合基础模型：

hm（x）=argminγ∑i=1NL（yi, Fm-1（xi）+γh（xi））

式中： hm（x）为第m轮迭代所拟合的基础模型; γ 为基础模型的系数; h（xi）为基础模型对样本 xi的预测值。

（4）将当前弱分类器加入到模型中进行预测, 并更新已有的模型：

Fm（x）=Fm-1（x）+αhm（x）

式中： α为学习率（也称为步长）, 控制每轮迭代时新模型的权重。

（5）生成最终模型：

F（x）=∑m=1Mαhm（x）

式中： F（x）为最终的梯度提升模型; M为迭代次数; α和 hm（x）分别为第m轮迭代的学习率和基础模型。

这些公式描述了梯度提升算法中的关键步骤：构建初始化模型、计算残差（负梯度）、拟合基础模型、更新已有的模型以及生成最终模型。通过迭代优化模型, 梯度提升算法能够逐步改进预测效果。

3.2 研究区实际应用

本文将基于GBDT预测储层物性参数的方法应用于鄂尔多斯盆地H油田的21口井, 该方法输入的测井曲线主要包括自然伽马、声波时差、密度、中子、电阻率, 其中共6口井有薄片分析结果, 用其中4口井与结合常规方法得出的15口井的物性数据进行训练, 然后预测另外2口井的孔隙度、渗透率结果并与岩心分析结果对照, 对照效果较好。

3.2.1 特征值的选择

根据文献调研和参考其他研究者的工作, 主要选择与目标变量相关性较大的特征来进行特征值的选取。本次针对孔隙度预测输入的特征曲线是声波时差、中子、密度, 图2是测井响应与孔隙度交会图, 其中声波时差与孔隙度拟合程度最高; 针对渗透率预测输入的特征曲线是密度、声波时差、自然伽马、中子、电阻率, 图3是测井响应与渗透率交会图, 其中密度、声波时差、自然伽马与渗透率的相关性较好, 其他较差。

图2 测井响应与孔隙度交会图

图3 测井响应与渗透率交会图

根据上面各个散点图显示的结果可知, 使用声波时差、中子和密度做为孔隙度预测的输入特征时, 声波时差与孔隙度拟合程度最高, 表明它在孔隙度预测中占据重要比例。预测渗透率时, 除了密度、声波时差和中子特征外, 自然伽马和电阻率特征也被引入作为输入特征, 其中密度和声波时差与渗透率拟合程度较高, 说明它们对于预测渗透率是重要的因素。

3.2.2 模型训练

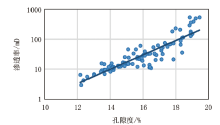
对H油田21口井的物性进行处理和分析, 共有6口井通过岩心薄片鉴定得到了结果, 利用其中4口井作为训练集, 将其砂岩段的声波时差与薄片分析的真实孔隙度进行交会分析（图2a）, 可见两者之间具有较好的线性关系; 将真实孔隙度与薄片分析的渗透率进行交会, 也具有较好的线性关系（图4）。

图4 孔隙度与渗透率交会图

利用最小二乘法（统计回归法和孔渗拟合法）建立孔隙度预测模型（r2=0.88）, 其模型公式为：

ϕ=0.2762Δt-50.969

建立渗透率预测模型（r2=0.87）, 其模型公式为：

K=0.0045e0.5507ϕ

式中：ϕ 为储层孔隙度, %; Δ t为声波时差, μ s/m; K为储层渗透率, mD。

根据该模型, 用作为训练集的4口井的声波时差可以初步估算其余15口井的储层孔隙度和渗透率。将除了测试集2口井外的19口井的孔隙度和渗透率与测井敏感属性参数作为算法的多元输入信息来训练梯度提升决策树, 并以岩心实验结果的孔隙度、渗透率作为标签, 建立目的层储层物性参数预测模型。

用相关系数作为预测结果的评价标准, 即：

r=∑i=1n（Pi-P-）（Ti-T-）∑i=1n（Pi-P-）2∑i=1n（Ti-T-）2

式中：r为相关系数; n为数据点个数; P、T分别为储层物性参数预测值和实际值; P-、 T-分别为储层物性参数预测值和实际值的均值。

本文基于GBDT的孔隙度、渗透率预测结果与岩心分析结果的r2均为0.9; 而最小二乘法在测试井计算的孔隙度、渗透率与岩心分析结果的相关系数也较高, r2分别为0.88和0.87。

3.2.3 结果展示

为了进一步提高梯度提升决策树的预测准确率, 可以将测井曲线拟合的孔隙度、渗透率和相关的测井响应作为梯度提升决策树算法的输入进行训练。使用被最小二乘法估算的参数所训练的梯度提升决策树, 可以更好地预测孔隙度和渗透率。图5为部分储层物性预测结果对比, 黄色部分代表实际的孔隙度和渗透率, 蓝色部分代表预测的孔隙度和渗透率, 可见该模型预测精度较高, 预测结果与岩心分析结果r2为0.93。

图5 储层物性预测结果对比

4 结论

（1）基于文献、调研, 储层物性参数常规预测方法很多, 岩石体积物理模型法、参数交会图法、统计回归法、核磁共振测井法、机器学习法等可以对孔隙度进行预测; 孔渗拟合法、Timur公式法、Herron模型、基于毛管压力、核磁共振测井法、地层因素法、斯通利波法等可以对储层渗透率进行预测, 其中孔渗拟合法较简单, 基于毛管压力、核磁共振测井法成本较高, 机器学习法前景较好。

（2）基于GBDT回归的储层物性参数预测的准确性依赖于输入参数的选择, 选取输入参数时要考虑其对预测目标的影响效果, 以便选出对物性影响较大的几个参数进行预测。与常规储层物性参数预测方法相比, 基于GBDT回归的储层物性参数计算方法准确率高、稳定性好, 结合常规线性拟合方法进行对比, 可进一步提高预测结果准确性。

（编辑 陈 娟）

参考文献
[1] 王亚兰, 杨凯程, 王河, 等. 苏南区块中子-密度交会计算孔隙度方法应用[J]. 石油化工应用, 2022, 41(9): 72-77.
WANG Yalan, YANG Kaicheng, WANG He, et al. Application of neutron-density intersection method to calculate porosity in southern Sulige block[J]. Petrochemical Industry Application, 2022, 41(9): 72-77. [本文引用:1]
[2] 田军, 刘永雷, 徐博, 等. 深埋储层孔隙度迭代反演方法[J]. 石油地球物理勘探, 2022, 57(3): 666-675.
TIAN Jun, LIU Yonglei, XU Bo, et al. Iterative inversion method of porosity in deep buried reservoir[J]. Oil Geophysical Prospecting, 2022, 57(3): 666-675. [本文引用:1]
[3] 张宇航, 时保宏, 张曰静, 等 . 机器学习方法在浅层滩坝相薄储层孔隙度预测中的应用: 以准噶尔盆地车排子地区白垩系为例[J/OL]. 沉积学报: 1-12[2023-03-21]. http://kns.cnki.net/kcms/detail/62.1038.P.20221026.1812.002.html.
ZHANG Yuhang, SHI Baohong, ZHANG Yuejing, et al. Application of machine learning method in porosity prediction of shallow beach-dam facies thin reservoir: A case study of Cretaceous in Chepaizi area of Junggar Basin[J/OL]. Acta Sedimentologica Sinica: 1-12[2023-03-21]. http://kns.cnki.net/kcms/detail/62.1038.P.20221026.1812.002.html. [本文引用:1]
[4] 魏国华, 韩宏伟, 刘浩杰, 等. 基于半监督高斯混合模型与梯度提升树的砂岩储层相控孔隙度预测[J]. 石油地球物理勘探, 2023, 58(1): 46-55.
WEI Guohua, HAN Hongwei, LIU Haojie, et al. Prediction of facies -controlled porosity of sand stone reservoir based on semi -supervised Gaussian mixture model and gradient boosting tree[J]. Oil Geophysical Prospecting, 2023, 58(1): 46-55. [本文引用:1]
[5] 张荣虎, 姚根顺, 寿建峰, 等. 沉积、成岩、构造一体化孔隙度预测模型[J]. 石油勘探与开发, 2011, 38(2): 145-151.
ZHANG Ronghu, YAO Genshun, SHOU Jianfeng, et al. Integrated porosity prediction model of sedimentation, diagenesis and structure[J]. Petroleum Exploration and Development, 2011, 38(2): 145-151. [本文引用:1]
[6] 杨丽, 覃利娟, 彭志春, 等. 乌石东区成岩演化数值模拟与孔隙度预测[J]. 地质科技通报, 2022, 41(3): 150-157.
YANG Li, QIN Lijuan, PENG Zhichun, et al. Numerical simulation of diagenetic evolution and porosity prediction in eastern Wushi area[J]. Bulletin of Geological Science and Technology, 2022, 41(3): 150-157. [本文引用:2]
[7] 韩宏伟, 刘浩杰, 桑文镜, 等. 基于半监督学习的井震联合储层横向孔隙度预测方法[J]. 地球物理学报, 2022, 65(10): 4073-4086.
HAN Hongwei, LIU Haojie, SANG Wenjing, et al. Prediction method of reservoir lateral porosity based on semi-supervised learning combined seismic with well logs[J]. Chinese Journal of Geophysics, 2022, 65(10): 4073-4086. [本文引用:2]
[8] 张言辉. 基于物性预测相对渗透率的改进神经网络方法[J]. 天然气与石油, 2020, 38(3): 44-49.
ZHANG Yanhui. Improved neural network method for predicting relative permeability based on physical properties[J]. Natural Gas and Oil, 2020, 38(3): 44-49. [本文引用:1]
[9] 曹茜, 王志章, 樊太亮, 等. 基于FSVM法分岩性解释砂砾岩储层渗透率[J]. 新疆大学学报(自然科学版), 2018, 35(3): 264-271.
CAO Qian, WANG Zhizhang, FAN Tailiang, et al. Permeability interpretation of sand y conglomerate reservoir by lithology based on FSVM method[J]. Journal of Xinjiang University(Natural Science Edition), 2018, 35(3): 264-271. [本文引用:1]
[10] 李雄炎, 秦瑞宝, 曹景记, 等. 复杂储层连通孔隙度评价与渗透率定量计算方法[J]. 石油地球物理勘探, 2022, 57(2): 377-385.
LI Xiongyan, QIN Ruibao, CAO Jingji, et al. Evaluation of connected porosity and quantitative calculation method of permeability in complex reservoirs[J]. Oil Geophysical Prospecting, 2022, 57(2): 377-385. [本文引用:1]
[11] 黄雨阳, 冯进, 宋伟, 等. 结合NMR横向弛豫时间谱与压汞资料的砂岩储层改进渗透率智能预测方法[J]. 物探化探计算技术, 2020, 42(3): 338-344.
HUANG Yuyang, FENG Jin, SONG Wei, et al. Improved intelligent permeability prediction method for sand stone reservoirs based on NMR transverse relaxation time spectrum and mercury injection data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2020, 42(3): 338-344. [本文引用:1]
[12] 杨坤, 王付勇, 曾繁超, 等. 基于数字岩心分形特征的渗透率预测方法[J]. 吉林大学学报(地球科学版), 2020, 50(4): 1003-1011.
YANG Kun, WANG Fuyong, ZENG Fanchao, et al. Permeability prediction method based on fractal characteristics of digital core[J]. Journal of Jilin University(Earth Science Edition), 2020, 50(4): 1003-1011. [本文引用:1]
[13] 王猛, 董宇, 蔡军, 等. 基于BP神经网络的储层渗透率预测及质量评价方法[J]. 地球物理学进展, 2023, 38(1): 321-327.
WANG Meng, DONG Yu, CAI Jun, et al. Reservoir permeability prediction and quality evaluation method based on BP neural network[J]. Progress in Geophysics, 2023, 38(1): 321-327. [本文引用:1]
[14] 谷宇峰, 张道勇, 鲍志东, 等. 利用梯度提升决策树(GBDT)预测渗透率: 以姬塬油田西部长4+5段致密砂岩储层为例[J]. 地球物理学进展, 2021, 36(2): 585-594.
GU Yufeng, ZHANG Daoyong, BAO Zhidong, et al. Permeability prediction using Gradient Boosting Decision Tree (GBDT): A case study of tight sand stone reservoir in Chang 4+5 Member in western Jiyuan Oilfield[J]. Progress in Geophysics, 2021, 36(2): 585-594. [本文引用:1]
[15] 谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37.
GU Yufeng, ZHANG Daoyong, BAO Zhidong, et al. Permeability prediction of logging data by PSO-XGBoost[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. [本文引用:1]
[16] 王谦, 谭茂金, 石玉江, 等. 径向基函数神经网络法致密砂岩储层相对渗透率预测与含水率计算[J]. 石油地球物理勘探, 2020, 55(4): 864-872.
WANG Qian, TAN Maojin, SHI Yujiang, et al. Relative permeability prediction and water cut calculation of tight sand stone reservoir by radial basis function neural network method[J]. Oil Geophysical Prospecting, 2020, 55(4): 864-872. [本文引用:1]
[17] 高强勇, 王昕, 高建英, 等. 致密岩心核磁共振孔隙度影响因素分析[J]. 测井技术, 2021, 45(4): 424-430.
GAO Qiangyong, WANG Xin, GAO Jianying, et al. Analysis of influencing factors of NMR porosity of tight core[J]. Well Logging Technology, 2021, 45(4): 424-430. [本文引用:1]
[18] 周新波, 段迎利, 袁伟, 等. M油田渗透率计算方法研究[J]. 科技创新与应用, 2014, 108(32): 76.
ZHOU Xinbo, DUAN Yingli, YUAN Wei, et al. Study on permeability calculation method of M Oilfield[J]. Technology Innovation and Application, 2014, 108(32): 76. [本文引用:1]
[19] 路萍, 王浩辰, 高春云, 等. 致密砂岩储层渗透率预测技术研究进展[J]. 地球物理学进展, 2022, 37(6): 2428-2438.
LU Ping, WANG Haochen, GAO Chunyun, et al. Research progress of permeability prediction technology for tight sand stone reservoirs[J]. Progress in Geophysics, 2022, 37(6): 2428-2438. [本文引用:1]
[20] 汤潇, 张超谟, 周文银, 等. Purcell模型与Thomeer模型相结合的高精度渗透率模型研究[J]. 当代化工, 2019, 48(12): 2934-2938.
TANG Xiao, ZHANG Chaomo, ZHOU Wenyin, et al. Study on high precision permeability model based on Purcell model and Thomeer model[J]. Contemporary Chemical Industry, 2019, 48(12): 2934-2938. [本文引用:1]
[21] 孙颖. 核磁共振在页岩储层参数评价中的应用综述[J]. 地球物理学进展, 2023, 38(1): 254-270.
SUN Ying. Application of nuclear magnetic resonance in shale reservoir parameter evaluation[J]. Progress in Geophysics, 2023, 38(1): 254-270. [本文引用:1]
[22] 胡婷婷, 贾春明, 余海涛, 等. 核磁共振测井法估算砂砾岩储层束缚水饱和度模型构建[J]. 核电子学与探测技术, 2020, 40(6): 897-901.
HU Tingting, JIA Chunming, YU Haitao, et al. Construction of model for estimating irreducible water saturation of glutenite reservoirs by nuclear magnetic resonance logging[J]. Nuclear Electronics & Detection Technology, 2020, 40(6): 897-901. [本文引用:1]
[23] 何玉春. 基于机器学习的储层渗透率预测方法[J]. 石化技术, 2022, 29(12): 182-184.
HE Yuchun. Prediction method of reservoir permeability based on machine learning[J]. Petrochemical Industry Technology, 2022, 29(12): 182-184. [本文引用:1]
[24] 沈夏炯, 张俊涛, 韩道军. 基于梯度提升回归树的短时交通流预测模型[J]. 计算机科学, 2018, 45(6): 222-227, 264.
SHEN Xiajiong, ZHANG Juntao, HAN Daojun. Short -term traffic flow prediction model based on gradient boosting regression tree[J]. Computer Science, 2018, 45(6): 222-227, 264. [本文引用:1]