引用本文
李阳, 郭明宇, 倪鹏勃, 李鸿儒, 符强, 黄子舰. 渤海海域井壁取心裂解烃 S2烃类损失恢复回归分析 [J]. 录井工程, 2024,35(2): 49-56.
LI Yang, GUO Mingyu, NI Pengbo, LI Hongru, FU Qiang, HUANG Zijian. Regression analysis of hydrocarbon loss restoration of cracking hydrocarbon S2 from sidewall coring in the Bohai Sea [J]. Mud Logging Engineering, 2024,35(2): 49-56.
Doi:10.3969/j.issn.1672-9803.2024.02.009  
Permissions
Copyright©2024, 《录井工程》杂志社
《录井工程》杂志社 所有
渤海海域井壁取心裂解烃 S2烃类损失恢复回归分析
李阳①, 郭明宇②, 倪鹏勃③, 李鸿儒②, 符强②, 黄子舰④
①中国石油辽河油田分公司勘探开发研究院
②中海石油（中国）有限公司天津分公司
③中法渤海地质服务有限公司
④盘锦中录油气技术服务有限公司

作者简介：李阳 1988年生,博士,2022年毕业于西南石油大学地质资源与地质工程专业,现为中国石油辽河油田分公司勘探开发研究院在站博士后,主要从事石油地质、数据挖掘等研究工作。通信地址：124010 辽宁省盘锦市兴隆台区石油大街95号中国石油辽河油田分公司勘探开发研究院。电话：17741949988。E-mail：7891235@qq.com

收稿日期: 2024-01-16
基金: 中海石油（中国）有限公司重大科技专项“渤海油田上产4000万吨新领域勘探关键技术”（编号：CNOOC-KJ 135 ZDXM36 TJ 08 TJ）
摘要

地化录井受工程、地质条件及人为因素的影响,往往造成岩石样品从井底到地表的烃类损失,不能很好地反映地下储层的真实含油气信息,因此需要一种合理准确的方法进行烃类损失恢复。针对渤海海域不同地区不同层位的岩屑值（自变量）与壁心值（因变量）之间的关系,基于最小二乘法、梯度下降法及其衍生算法,以多元线性回归和非线性回归两种方式来拟合研究区井壁取心数据。多元线性回归模型可使用标准方程法、岭回归、LASSO（Least Absolute Shrinkage and Selection Operator）及弹性网进行回归拟合,非线性回归模型可使用梯度下降法和分段函数的拟合方法。对不同回归分析方法进行分析对比可知,岭回归在计算线性关系的烃类损失方面具有较好的效果,决定系数 r2均超过0.7;基于岭回归分段函数拟合和非线性回归模型 y= x/（ b+ kx）适合非线性烃类损失恢复。与传统的烃类损失恢复方法相比,使用量化的方式对研究区烃类进行恢复,更加科学全面,具有广泛的应用前景。

关键词: 烃类损失恢复; 裂解烃; 回归分析; 多元线性回归模型; 非线性回归模型 井壁取心
中图分类号:TE132.1 文献标志码:A
Regression analysis of hydrocarbon loss restoration of cracking hydrocarbon S2 from sidewall coring in the Bohai Sea
LI Yang①, GUO Mingyu②, NI Pengbo③, LI Hongru②, FU Qiang②, HUANG Zijian④
①Exploration and Development Research Institute, Liaohe Oilfield of CNPC, Panjin, Liaoning 124010, China
②Tianjin Branch of CNOOC（China） Co., Ltd., Tianjin 300452, China
③China French Bohai Geoservices Co., Ltd., Tianjin 300457, China
④Panjin Zhonglu Oil & Gas Technology Service Co., Ltd., Panjin, Liaoning 124010,China;
Abstract

Geochemical logging is often affected by engineering, geological conditions, and human factors, resulting in hydrocarbon losses of rock samples from the bottom of the well to the surface. It fails to reflect the real oil and gas content information of underground reservoirs well, and a reasonable and accurate method is needed to restore hydrocarbon losses. In view of the relationship between cuttings values（independent variables） and wall core values （dependent variables） at different horizons in different areas of the Bohai Sea, based on least square method, gradient descent method and its derivative algorithm, the paper fits the data of sidewall coring in the study area using two methods： multiple linear regression and non-linear regression. The model of multiple linear regression can be fitted by regression using normal equation, ridge regression, LASSO （Least Absolute Shrinkage and Selection Operator） and elastic net. The non-linear regression model can use the gradient descent method and the piecewise function fitting method. The analysis and comparison of different regression analysis methods show that ridge regression has good results in calculating the hydrocarbon losses of linear relationship, with the determination coefficient r2 exceeding 0.7. Piecewise function fitting based on ridge regression and nonlinear regression model y= x/（ b+ kx） are suitable for non-linear hydrocarbon loss restoration. Compared with the traditional method of hydrocarbon loss restoration, using the quantitative method to restore hydrocarbons in the study area is more scientific and comprehensive, and has a broad prospect of application.

Keyword: hydrocarbon loss restoration; cracking hydrocarbon; regression analysis; multiple linear regression model; non-linear regression model; sidewall coring
0 引言

回归分析源于19世纪初的天文学, 其最早形式是最小二乘法, 而后20世纪50年代, 计算机技术促进了回归分析相关算法和软件的发展, 进而使得回归分析开始向多元回归、非线性回归和广义线性模型等方向扩展, 以满足解决更多实际问题的需求。21世纪以来, 随着大数据和机器学习的发展, 回归分析仍然保持着重要地位, 并在各领域继续发挥着重要作用。近些年, 各学者使用回归分析方法在油气勘探中取得了丰富的研究成果, 纵观回归分析在油气勘探中的应用, 主要体现在两个方面：（1）储层物性计算及优质储层预测, 其中多数学者选用矿物含量或测井数据（如声波时差、密度、中子、自然伽马等）使用多元线性回归模型来对储层的孔隙度和渗透率进行预测[1, 2, 3, 4, 5, 6], 也有学者使用多元逐步回归、偏最小二乘回归来对多种地震属性进行分析, 从而达到砂体厚度与优质储层预测的目的[7, 8, 9, 10, 11, 12]; （2）原始有机碳恢复, 利用测井数据、烃源岩地球化学特征（不溶残碳、有机质类型及成熟度）以及元素地球化学等数据使用多元线性回归模型可以很好地解决原始有机碳恢复问题, 与改进的Δ logR和CARBOLOG等方法相比, 多元线性回归方法计算效果更加有效[13, 14, 15, 16, 17, 18]。

地球化学录井作为一种现场快速定量分析技术, 在发现油气显示、评价油气水层等方面发挥了重要作用。岩屑是地球化学录井中最方便、廉价的分析对象, 但岩屑在从井底返回井口的过程容易受钻井液冲刷、温度与压力变化等因素影响, 造成大量的烃类损失; 井壁取心和岩心的烃损量较小, 接近地层原始烃类含量, 缺点是这两种取样方式成本较高。基于回归分析方法可以建立烃类损失恢复方法, 来更准确地描述地层的原始烃类含量。综合渤海海域二级构造带中不同层位岩屑值（自变量）与壁心值（因变量）之间的关系, 岩屑与壁心呈线性关系时采用最小二乘法以及有偏回归算法（岭回归、LASSO及弹性网）, 使用多元线性回归对研究区的烃类损失进行多元线性拟合; 岩屑与壁心呈非线性关系时, 使用梯度下降法和基于岭回归的分段函数拟合这两种方法实现烃类损失恢复。研究成果综合考虑自变量与因变量的关系, 针对线性关系和非线性关系选择不同的回归模型来构建岩屑与壁心之间的近似解析式, 以达到烃类损失恢复的目的。

1 区域地质概况

渤海海域地理位置位于渤海湾盆地中东部, 在大地构造位置上, 渤海地区位于华北新生代裂谷盆地, 东邻胶辽断隆区, 西为黄骅坳陷的延伸, 北与下辽河坳陷相连, 南与济阳坳陷相接, 是渤海湾盆地的重要组成部分, 面积约为4.2× 104 km2。渤海海域与陆地部分相比, 其主要地质特点是新生代地层发育, 喜山运动使地壳抬升并遭受剥蚀夷平, 渤海结束了以古近纪湖相沉积为主的历史, 开始了以河流相为主的发展过程。断裂构造主活动期晚, 有很多断裂至今仍在活动, 渤海海域包括济阳、黄骅、渤中、辽东湾坳陷和埕宁隆起5个一级构造单元, 包括由13个凸起、4个低凸起、18个凹陷构成的35个二级构造单元, 研究选取辽中凹陷、辽西低凸起、渤中凹陷、黄河口凹陷、莱北低凸起以及庙西北凸起6个重点二级构造单元的沙河街组、东营组、馆陶组和明化镇组来进行烃类损失恢复研究。

2 基于回归分析的烃类损失恢复
2.1 线性回归烃类损失恢复

2.1.1 线性回归模型建立

标准方程法是一种简单而有效的求解线性回归问题最优解的方法, 它基于最小二乘法来求取全局最优解, 为解决小样本特征参数比样本点多而导致矩阵XTX（其中X为自变量样本矩阵）不可逆以及各个特征参数多重共线的问题。在标准方程法代价函数的基础上加入正则项, 进而得到岭回归、LASSO以及弹性网回归3种有偏估计回归模型。

受岩心热解资料相对较少的限制, 在此仅作岩屑热解参数向井壁取心热解参数的回归, 即将岩屑热解参数恢复到井壁取心热解参数。

通过整理渤海海域多个二级构造带（包括辽中凹陷、辽西低凸起、渤中凹陷、黄河口凹陷、莱北低凸起以及庙西北凸起）中102口井的岩屑与井壁取心热解参数的裂解烃S2数据, 观察岩屑与壁心的相同热解参数构成的散点图发现, 渤海海域内辽东湾坳陷（包含各个次级构造）、渤中凹陷、黄河口凹陷及莱州湾凹陷沙河街组至馆陶组中, 尤其是中质油（原油密度介于0.87~0.92 g/cm3）地层, 其多数岩屑值与壁心值呈线性变化的关系。

选取研究区中10组烃类数据, 分别是岩屑热解中的S1、S2及含油气总量（Pg）、油产率指数（OPI）、油气总产量指数（TPI）, 来拟合研究井壁取心热解参数中的裂解烃S2。针对这些线性关系, 分别使用标准方程法、岭回归、LASSO以及弹性网, 选用不同数量自变量建立烃类损失恢复线性回归模型（表1）, 对这10组数据进行分析实验。

表1 烃类损失恢复线性回归模型

从10组数据使用不同方法分析得到的相关系数折线图中可以发现, 使用多个岩屑自变量的拟合效果均好于一元线性回归（图1）; 标准方程法中相关系数随自变量数量的增加而增大, 原因在于当特征参数增加时容易发生过度拟合, 尤其是在小样本集中（如莱北低凸起东营组中质油的数据点仅有31个）。此外, 其他3种有偏估计回归法拟合的相关系数在使用两个自变量后变化不大, 尤其是LASSO与弹性网, 四元回归与五元回归相关系数不再变化, 说明这两种回归方法在很大程度上解决了多重共线的问题, 因为Pg、OPI与TPI均是由S0、S1及S2计算得到（其中S0一般可忽略不计）。

图1 线性回归分析相关系数折线图

相关系数r计算公式如下：

$r=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}$

式中： Cov（X，Y）为样本X和Y的协方差; σ X、 X̅分别为X的标准差和平均值; σ Y、 Y̅分别为Y的标准差和平均值; n为样本个数, i=1, 2, …, n。

2.1.2 多元线性回归模型评估

在以上分析基础上, 选用M 2-M 5多元线性回归模型, 将每组数据集按照7∶ 3的比例划分为训练集和测试集, 使用标准方程法、岭回归、LASSO及弹性网4种回归方法对10组数据以交叉验证的方式进行分析拟合, 使用均方根误差（RMSE）以及决定系数（R2）来对模型的拟合性能进行评估, 均方根误差越小, 决定系数越大, 拟合效果越好, 最终选取适合研究区的拟合模型。

从图2中可以发现, 在进行二元线性拟合时, 4种回归方法决定系数差异不大, 但LASSO和弹性网均方根误差的上四分位数较大, 说明LASSO和弹性网整体误差偏大, 回归效果差于标准方程法和岭回归; 在使用更多参数进行拟合时, 岭回归在均方根误差及决定系数上均优于其他3种回归方法, 标准方程法由于发生过度拟合导致其拟合效果变差, 而LASSO和弹性网是将OPI和TPI此类的多重共线参数直接忽略掉, 导致其3次拟合效果变化不大。M 4模型与M 5模型, 岭回归拟合效果较为相近, 但M 4模型的均方根误差以及决定系数整体上优于M 5模型, 因此, 笔者选用岭回归法的M 4模型对研究区10组数据进行拟合。从图3、表2中可以发现, 10组数据的实测值与预测值相关性较好, 决定系数均大于0.7, 同时具有较小的均方根误差, 使用岭回归方法计算得到的预测值与井壁取心的实测值匹配效果较好。

图2 4种不同方法的均方根误差与决定系数箱形图

图3 基于岭回归M 4模型计算的井壁取心S2预测值与实测值对比

表2 应用岭回归法M 4模型拟合效果一览表

$R M S E=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i}\right)^{2}}$

$R^{2}=1-\frac{\sum_{i=1}^{n}\left(Y_{i}-\hat{Y}_{i}\right)^{2}}{\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}$

式中：Yi为Y的真实值; Ŷi为Y的预测值。

2.2 非线性回归模型烃类损失恢复

研究区部分层位及油质的岩屑与壁心的热解参数值呈现非线性的变化规律, 具体表现为壁心值开始上升速度快, 然后变慢, 这主要是因为在此类样品中部分储层的砂岩以泥质胶结为主, 疏松易碎, 容易发生烃类散失。非线性回归与线性回归相比更为复杂, 为此, 笔者选用梯度下降法和基于岭回归的分段函数拟合法来解决非线性的烃类损失校正。

2.2.1 梯度下降法

梯度下降法通过初始化回归系数并对系数进行调整, 可以计算代价函数的极小值或最小值, 进而确定最优回归系数。在使用梯度下降法对研究区非线性变化的烃类进行烃类损失校正时, 首先需要选取合适的函数模型, 经研究发现, y=x/（b+kx）与y=b（1-e-kx）这两种函数模型和岩屑与壁心的热解参数值的变化规律较为相符。使用梯度下降法寻找函数模型中合适的b、k参数值, 来使总误差达到最小, 设置初始值（0.01, 0.2）, 学习率为0.1, 不断更新（b, k）的数值, 直至总误差最小。

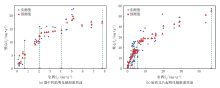
从庙西北凸起明化镇组重质油和渤中凹陷明化镇组重质油的曲线拟合效果来看, 两种函数模型的拟合效果比较接近（图4）; 但从表3的RMSE和R2两项评价指标来看, 函数模型y=x/（b+kx）的拟合效果要优于函数模型y=b（1-e-kx）。同时, 通过对比两种模型的迭代次数可以发现, 函数模型y=x/（b+kx）比函数模型y=b（1-e-kx）更容易收敛达到模型的极小值。因此, 在使用梯度下降法对研究区进行非线性烃类损失校正时, 选用函数模型y=x/（b+kx）, 更加准确合理。

图4 研究区岩屑与壁心基于梯度下降法非线性回归效果

表3 基于梯度下降法的非线性回归模型烃损恢复拟合效果

使用梯度下降法对研究区呈非线性关系的烃类损失恢复时, 需要选取合适的非线性函数模型, 且不同模型的回归效果也千差万别, 能找到一个较为合适的函数模型较为困难。

2.2.2 基于岭回归的分段函数拟合法

分段函数拟合法的基本思想是将非线性拟合变成线性拟合, 同时上文已述, 在使用岭回归进行多元线性回归时具有较好的拟合效果, 因此笔者选用了一种基于岭回归的分段函数拟合方法, 来对研究区的非线性烃类损失进行恢复校正。将分段函数分成N个区间, 保证每个区间的样本数相同, 为n个, 或者前N-1个区间样本数为n个, 最后一个区间样本数大于n个（此时为样本集个数未整除n）, 确定分段函数每个区间后, 使用岭回归的方法对每个区间的样本点进行多元线性拟合, 并且选取合适的样本数n, 使得回归模型具有较小的RMSE。

本文利用基于岭回归的分段函数拟合方法, 对研究区渤中凹陷明化镇组重质油和庙西北凸起明化镇组重质油的烃类损失进行了校正（前者每个区间13个数据点, 后者每个区间8个数据点）, 不难发现, 此种方法拟合效果优于梯度下降法, 使得研究区两个区域的烃类损失校正具有更小的RMSE和更大的R2（图5、表4）; 而且, 与梯度下降法相比, 使用基于岭回归的分段函数拟合方法不用再寻找合适的非线性函数模型。

图5 基于岭回归的分段函数拟合回归效果

表4 基于岭回归分段拟合效果一览表
3 结论

（1）在油气勘探的多数领域中回归分析被广泛应用, 根据自变量与因变量之间的关系（线性或非线性）, 选取合适的回归分析模型, 可提升研究成果的准确性, 做好自变量和因变量两种类型数据之间对应关系是建立回归模型数据准确性的基础。

（2）中质油的岩屑与壁心烃类损失多呈线性相关关系, 采用标准方程法、岭回归、LASSO及弹性网回归分析方法进行对比分析, 拟合效果均优于一元线性回归模型, 最后确定M 4模型为最佳拟合模型, 使用岭回归对研究区的烃类损失进行了恢复校正。

（3）重质油的岩屑与壁心烃类损失一般呈非线性相关关系, 选用梯度下降法和基于岭回归的分段函数拟合法进行非线性烃类损失恢复, 函数模型y=x/（b+kx）比y=b（1-e-kx）更符合研究区内岩屑与壁心的变化规律; 与梯度下降法相比, 基于岭回归的分段函数拟合法在进行非线性烃类损失校正中具有更好的拟合效果。

编辑 陈娟

参考文献
[1] 陈俊霖, 王朋, 郜元元, 等. 多元逐步回归法在致密砂岩储层矿物与孔隙度关系分析中的应用: 以鄂尔多斯盆地姬塬地区长8储层为例[J]. 天然气地球科学, 2021, 32(9): 1372-1383.
CHEN Junlin, WANG Peng, GAO Yuanyuan, et al. Application of multiple stepwise regression method in the analysis of the relationship between porosity and tight sand stone: Case study of Chang 8 reservoir in Jiyuan area, Ordos Basin[J]. Natural Gas Geoscience, 2021, 32(9): 1372-1383. [本文引用:1]
[2] 马小伟. 鄂尔多斯盆地临兴地区盒8段储层特征研究[D]. 青岛: 山东科技大学, 2018.
MA Xiaowei. Study on reservoir characteristics of the eighth member, Shihezi Formation in Lixing area, Ordos Basin, NW China[D]. Qingdao: Shand ong University of Science and Technology, 2018. [本文引用:1]
[3] 徐士鹏, 马崇尧, 王娜, 等. 卡拉库里区块碳酸盐岩沉积相分布特征研究[J]. 新疆石油天然气, 2020, 16(3): 1-5.
XU Shipeng, MA Chongyao, WANG Na, et al. Study on the distribution characteristics of carbonate sedimentary facies in Karakul block[J]. Xinjiang Oil & Gas, 2020, 16(3): 1-5. [本文引用:1]
[4] 范雯. 逐步回归分析方法在储层参数预测中的应用[J]. 西安科技大学学报, 2014, 34(3): 350-355.
FAN Wen. Application of stepwise regression analysis method in reservoir parameter prediction[J]. Journal of Xi’an University of Science and Technology, 2014, 34(3): 350-355. [本文引用:1]
[5] 胡作维, 黄思静, 王冬焕, 等. 多元逐步回归分析在评价孔隙结构对低渗透砂岩储层质量影响中的应用[J]. 桂林理工大学学报, 2013, 33(1): 21-25.
HU Zuowei, HUANG Sijing, WANG Donghuan, et al. Application of multiple stepwise regression to influential evaluation of pore-throat size on low-permeability sand stone reservoirs[J]. Journal of Guilin University of Technology, 2013, 33(1): 21-25. [本文引用:1]
[6] 沈立成, 黄思静, 刘洁, 等. 用多元逐步回归方法评价储层孔隙度的控制因素[J]. 成都理工学院学报, 2002, 29(6): 610-616.
SHEN Licheng, HUANG Sijing, LIU Jie, et al. Estimation of controlling factors of reservoir porosity by using multiple stepwise regression analysis[J]. Journal of Chengdu University of Tehcnology, 2002, 29(6): 610-616. [本文引用:1]
[7] 刘艺萌, 张藜, 王志萍, 等. 沉积模式约束下复杂构造带砂体定量表征与沉积微相刻画: 以沙南凹陷曹妃甸18-1油田围区为例[J]. 大庆石油地质与开发, 2020, 39(1): 26-34.
LIU Yimeng, ZHANG Li, WANG Zhiping, et al. Quantitative characterization of the sand bodies and sedimentary microfacies description for the complicated structure belt with the restriction of the sedimentary model: Taking CFD oilfield 18-1 in Shanan sag as an example[J]. Petroleum Geology & Oilfield Development in Daqing, 2020, 39(1): 26-34. [本文引用:1]
[8] 徐江楠. 港东二区六断块新近系三维地质建模及应用[D]. 北京: 中国石油大学(北京), 2020.
XU Jiangnan. 3D geological modeling and application of the Neogene in fault-block 6 of No. 2 area, Gangdong oilfield[D]. Beijing: China University of Petroleum(Beijing), 2020. [本文引用:1]
[9] 马磊. 致密储层地震预测方法研究[D]. 大庆: 东北石油大学, 2016.
MA Lei. Study on seismic prediction method of tight reservoir[D]. Daqing: Northeast Petroleum University, 2016. [本文引用:1]
[10] 程顺国. 基于地质模式的多元地震属性储层预测[J]. 大庆石油地质与开发, 2014, 33(3): 151-154.
CHENG Shunguo. Prediction of multiple seismic attribute reservoir based on geological modes[J]. Petroleum Geology & Oilfield Development in Daqing, 2014, 33(3): 151-154. [本文引用:1]
[11] 李操. 基于地震属性的储层预测方法研究及初步应用[D]. 大庆: 大庆石油学院, 2006.
LI Cao. Reservoir parameter predicted method research and primary application basing on seismic attribute[D]. Daqing: Daqing Petroleum Institute, 2006. [本文引用:1]
[12] 刘国明, 董敏煜, 苑书金, 等. 储层横向预测的多元地质统计方法[J]. 石油地球物理勘探, 1999, 34(5): 555-559.
LIU Guoming, DONG Minyu, YUAN Shujin, et al. Multivariate geologic statistical method for horizontal reservoir prediction[J]. Oil Geophysical Prospecting, 1999, 34(5): 555-559. [本文引用:1]
[13] 王亚森. 河南中部W区块山西组页岩气储层测井评价[D]. 西安: 西安石油大学, 2020.
WANG Yasen. Well logging evaluation of Shanxi Formation shale gas reservoir in block W, central Henan[D]. Xi’an: Xi’an Shiyou University, 2020. [本文引用:1]
[14] 刘晓雪. 四川盆地典型地区富有机质页岩含气性测井评价[D]. 北京: 中国石油大学(北京), 2020.
LIU Xiaoxue. Well logging evaluation of gas content of organic-rich shale in typical areas of Sichuan Basin[D]. Beijing: China University of Petroleum(Beijing), 2020. [本文引用:1]
[15] 尚飞, 刘峥君, 解习农. 有机碳含量测井预测方法在泌阳凹陷的应用[J]. 新疆石油地质, 2016, 37(1): 102-106.
SHANG Fei, LIU Zhengjun, XIE Xinong. Application of well logs prediction method for organic carbon content in Biyang sag, Nanxiang basin[J]. Xinjiang Petroleum Geology, 2016, 37(1): 102-106. [本文引用:1]
[16] 郑一丁. 鄂尔多斯盆地东南部张家滩页岩元素地球化学特征及评价[D]. 青岛: 中国石油大学(华东), 2015.
ZHENG Yiding. Geochemical characteristics and evaluation of zhangjiatan shale elements in the southeast of Ordos Basin[D]. Qingdao: China University of Petroleum (East China), 2015. [本文引用:1]
[17] 尚飞. 泌阳凹陷古近系核三段富有机质页岩非均质性及控制因素分析[D]. 北京: 中国地质大学, 2015.
SAHNG Fei. Analysis of heterogenicity and control factors of organic-rich shale in He-3 Member, Biyang sag[D]. Beijing: China University of Geosciences, 2015. [本文引用:1]
[18] 王子文, 赵锡嘏, 卢双舫, 等. 原始有机质丰度的恢复及其意义[J]. 大庆石油地质与开发, 1991, 10(4): 20-26.
WANG Ziwen, ZHAO Xigu, LU Shuangfang, et al. The recovery of original abundance of organic matter and its significance[J]. Petroleum Geology & Oilfield Development in Daqing, 1991, 10(4): 20-26. [本文引用:1]