引用本文
屈凯旋, 于春勇, 彭力, 孙皓, 孙春辉. 基于灰色关联法和主成分分析法的致密砂岩储层流体性质测井解释评价方法[J]. 录井工程, 2024,35(3): 89-97.
QU Kaixuan, YU Chunyong, PENG Li, SUN Hao, SUN Chunhui. Logging interpretation and evaluation method for fluid properties of tight sandstone reservoirs based on grey relational and principal component analysis[J]. Mud Logging Engineering, 2024,35(3): 89-97.
Doi:10.3969/j.issn.1672-9803.2024.03.013  
Permissions
Copyright©2024, 《录井工程》杂志社
《录井工程》杂志社 所有
基于灰色关联法和主成分分析法的致密砂岩储层流体性质测井解释评价方法
屈凯旋①, 于春勇②, 彭力③, 孙皓①, 孙春辉①
①中国石油渤海钻探油气合作开发分公司
②中国石油渤海钻探第一录井公司
③中国石油渤海钻探泥浆技术服务分司

作者简介：屈凯旋 工程师,1993年生,2022年博士毕业于中国地质大学（北京）矿产普查与勘探专业,现在中国石油渤海钻探油气合作开发分公司从事致密砂岩气储层开发地质研究工作。通信地址：300457 天津市开发区第二大街83号（中国石油天津大厦）。电话：18811170326。E-mail：qukaixuan@cnpc.com.cn

收稿日期: 2024-07-24
基金: 国家科技重大专项“上古生界海陆过渡相页岩气赋存机理与富集规律研究”（编号：2016ZX05034-001）; 中国石油渤海钻探工程公司重大工艺研究项目“苏里格西区构造-岩性复合气藏富集成因机理与储层流体性质识别技术研究”（编号：2023ZD19Y）联合资助
摘要

苏里格气田致密砂岩气藏储层非均质性强,气水关系复杂,流体测井响应特征不明显,导致常规测井参数交会图法对储层流体性质的识别符合率较低,且容易引起误判,严重制约了气田的勘探开发。基于灰色关联法和主成分分析法,建立了一种致密砂岩储层流体性质测井解释新方法,并利用苏20区块西南部30口井112个试气层位资料对该方法的准确性进行了验证。首先利用灰色关联法优选出对储层流体性质变化反映最为敏感的声波时差、补偿密度、补偿中子、孔隙度和声波时差-补偿中子曲线幅度差（ A1）共5种测井响应参数,在此基础上,开展主成分分析,构建了 Y1- Y5共5个相互独立的主成分变量,并选取累计方差贡献率为86.99%的主成分 Y1和 Y2来综合反映多维测井变量的原始信息,最后,利用Fisher线性判别法,建立了气水定量解释模型。应用新方法结合多种测井敏感参数信息对储层流体性质进行识别,整体解释符合率为86.6%,气层解释符合率达到92.3%,相对常规交会图法均有明显提升。同时,新方法在研究区盒8段实际应用中效果显著,进一步表明新方法能够为研究区致密气藏的高效开发提供有效的技术支撑。

关键词: 灰色关联; 主成分分析; 测井曲线; 致密砂岩储层; 流体识别
中图分类号:TE132.1 文献标志码:A
Logging interpretation and evaluation method for fluid properties of tight sandstone reservoirs based on grey relational and principal component analysis
QU Kaixuan①, YU Chunyong②, PENG Li③, SUN Hao①, SUN Chunhui①
①Oil & Gas Cooperation and Development Company, BHDC, CNPC,Tianjin 300457, China
②No.1 Mud Logging Company, BHDC, CNPC, Tianjin 300280, China
③Mud Service Company, BHDC, CNPC, Tianjin 300280, China
Abstract

Due to the significant heterogeneity and intricate gas-water relation of the tight sandstone gas reservoirs in Sulige Gas Field, there is a limited distinction in fluid logging response characteristics. Consequently, this leads to a low coincidence rate in identifying the reservoir fluid properties for the conventional logging parameters cross-plot interpretation methods, making it challenge to effectively identify gas layers. A new gas-water identification method for tight sandstone reservoirs is established based on grey relational and principal component analysis methods. 112 gas test reservoirs from 30 wells in the southwestern part of Su 20 block are selected as analysis samples. First, the grey relational method is used to select 5 logging response parameters, which are the most sensitive to the change of reservoir fluid properties, namely interval transit time, compensated density, compensated neutron, porosity and the difference（ A1） in amplitude between internal transit time and compensated neutron curves. On this basis, principal component variables from Y1 to Y5 independent from each other are constructed based on the principal component analysis method, and principal components Y1 and Y2, with a cumulative variance contribution rate of 86.99%, are selected to synthesize the raw information reflecting the multidimensional logging variables. Finally, Fisher linear discriminant method is used to establish a gas-water quantitative interpretation model. The new method recognizes the reservoir fluid properties by integrating the information of multiple logging sensitive parameters, the overall interpretation compliance rate is 86.6%, and the gas layer interpretation compliance rate reaches 92.3%, which is an obvious improvement in the recognition efficiency compared with the conventional crossplot chart method. At the same time, the new method is effective in practical application on Member 8 of Shihezi Formation, which further indicates that the new method can provide effective technical support for the efficient development of tight gas reservoirs in the study area.

Keyword: grey correlation; principal component analysis; log; tight sandstone reservoir; fluid identification
0 引言

苏里格气田致密砂岩气资源规模巨大, 2022年产气量超300× 108 m3, 是当前我国非常规天然气规模开发和持续稳产的重要力量[1, 2, 3]。但该气田历经20余年的勘探开发, 富集区天然气储量已基本动用, 开发目标逐渐向外围气水混合区及富水区储量扩展, 其储层物性变差, 非均质性更强, 气水关系更加复杂。气井投产后普遍出现压力和产气量下降快、气水同产并存在井筒积液的情况, 且低产低效井占比持续升高, 给气田长期稳产带来极大困难[4, 5, 6]。因此, 开展储层气水识别研究, 优化开发层位, 实现先期有效控水, 对于高效开发气藏和提高储量动用程度具有重要意义。

测井信号是储层岩性、物性、含油气性的综合反映, 根据不同流体性质储层的测井响应特征参数建立交会图板, 是目前苏里格气田储层气水识别最直接和最常用的手段之一[7, 8]。然而, 由于致密砂岩储层通常具有低孔低渗、孔隙结构复杂、非均质性强、气水分布不均且束缚水含量高等特征, 高阻水层和低阻气层异常现象显著, 导致流体测井响应特征不明显, 气层、气水同层、含气水层、水层的测井响应关系并无明显规律可循, 常规交会图法适应性较差[9, 10, 11, 12, 13]。此外, 常规交会图法往往只能同时采用2至3种测井参数对气层进行评价, 参数指标数量少。同时, 由于不同类型测井参数对储层流体性质的敏感性不同, 且彼此之间可能存在一定的相关性, 这都会给储层流体性质的识别带来一定的复杂性和多解性, 导致对气层的解释出现误判、漏判的情况。主成分分析法能够同时提取多种测井参数的主成分信息, 并能通过数学降维将多个原始测井变量转变为少数几个彼此相互独立的综合测井变量, 同时能够最大限度保留数据样本的原始信息[14]。本文基于灰色关联法和主成分分析法, 建立了一种综合多种测井响应特征的致密砂岩储层流体性质识别方法, 以期通过提高储层流体性质识别准确率, 为苏里格气田高效开发提供技术支撑。

1 研究区概况

研究区位于苏里格气田苏20区块, 区块构造形态总体呈东西向展布的宽缓斜坡构造, 局部发育有低幅度（构造幅度< 20 m）的背斜构造。气藏主力开发层位为上古生界二叠系山西组山1段和下石盒子组盒8段。该区沉积相类型多样, 储层岩石成分复杂, 岩性变化大, 主要为石英砂岩和岩屑石英砂岩。由于砂岩储层经历过强烈的成岩改造作用, 孔隙类型整体以次生溶孔为主, 残余粒间孔及晶间孔次之, 孔喉组合类型多为中孔中喉型和中孔细喉型。储层孔隙度和渗透率的主要分布范围分别为2%~16%和0.01~10 mD, 总体上属于低渗-致密储层。

由于受到储层致密、岩性和物性变化大、孔隙结构复杂、非均质性强以及天然气充注强度低等地质因素影响, 储层气水关系复杂且流体的测井响应特征不明显。图1为苏20区块西南部30口井112个试气层段（其中包括65个气层、7个差气层、18个气水同层、13个含气水层和9个水层）常规测井参数交会图。从图1可以看出, 研究区不同流体性质储层电性特征无明显差别, 高、低阻气、水层并存, 数据点之间交叉重叠现象严重, 难以划分出明显的数据边界。利用常规交会图法识别气、水层, 不仅符合率低, 而且容易引起误判, 亟需进一步探索新的储层流体解释方法。

图1 苏20区块西南部不同流体性质储层常规测井参数交会图

2 方法简介
2.1 灰色关联法

灰色关联法是一种利用部分已知信息来研究和预测系统未知信息的多因素数学统计法, 主要是用来评价系统中母因素与子因素之间的关联性, 并通过计算因素间的灰色关联度来判断出引起母量变化的主要因素, 从而实现对系统动态发展和变化趋势的定量分析[15, 16, 17]。其主要分析步骤如下。

2.1.1 确定母、子序列

基于被评价目标事物的影响因素分析, 选取最能反映目标事物特性的主影响因素作为母因素, 其余的次影响因素作为子因素。将母、子因素数据按照一定顺序进行排列, 分别构成母序列 Xt0（0）和子序列 Xt0（i）, 其中t=1, 2, …, n; 其中i=1, 2, …, m。

2.1.2 构建评价矩阵

（1）构建原始评价矩阵。根据确定的母序列式和子序列式, 以母序列在前、子序列在后的顺序进行排列, 可构成一个n× （m+1）原始数据评价矩阵：

X0（0）=X10（0）X10（1）⋯X10（m）X20（0）X20（1）⋯X20（m）⋮⋮⋱⋮Xn0（0）Xn0（1）⋯Xn0（m）（1）

（2）构建标准化评价矩阵。由于不同序列原始数据的物理性质和意义存在差异, 为了消除因参数之间量纲和数量级的不同对预测结果造成的影响, 需要对母、子序列数据进行无量纲化处理, 获得具有可比性的标准化数据序列（2）, 处理方法主要包括极差化法、均值化法和极大值标准化法等。

X1（0）=X11（0）X11（1）⋯X11（m）X21（0）X21（1）…X21（m）⋮⋮⋱⋮Xn1（0）Xn1（1）…Xn1（m）（2）

2.1.3 计算母、子因素的相关系数及相关度

基于标准化后的评价矩阵, 通过下式可以计算出母、子因素之间的相关系数：

ξi，0=Δmin+ρΔmaxΔt（i，0）+ρΔmax，i=1，2，…，m（3）

其中： Δt（i，0）=Xt1（i）-Xt1（0）

Δmax=maxtmaxiXt1（i）-Xt1（0）

Δmin=mintminiXt1（i）-Xt1（0）

式中： Δt（i，0）为标准化后第i个子因素与母因素之间的绝对差值; Δmax和 Δmin分别为标准化后第i个子因素与母因素之间的绝对差值的最大值和最小值; ρ 为分辨系数, 取值范围一般为0~1, 为了减弱母、子序列之间因绝对差值太大而降低数据分析准确性的影响, 并提高灰色关联系数之间的差异性, 本次研究中分辨系数取0.5。

关联度指各子因素与母因素之间的相似程度, 其值介于0~1之间[18]。关联度越趋近于1, 说明子因素对母因素的作用越强, 彼此之间关系越密切, 反之亦然。根据相关系数的计算结果, 利用下式可以得出各因素的关联度：

${{r}_{i,0}}=\frac{1}{n}\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\xi }_{i0}}$（4）

式中：${{r}_{i,0}}$为第i个子因素与母因素的灰色关联度; n为样本数量。

2.2 主成分分析法

主成分分析法是一种将多维变量数据通过正交变换转换成少数几个彼此间互不相关的综合变量的数学降维方法[19]。该方法能够在损失很少初始信息的前提下, 将高维数据浓缩成几个主成分来综合反映原始数据所包含的全部信息, 从而达到简化数据结构和提高数据信息集中度的目的[20]。其分析步骤如下。

（1）初始矩阵构成。在数学降维过程中, 初始变量的总方差保持不变, n个初始变量即有n个主成分[21]。设目标系统的样本数为n, 每个样本具有p个特征变量x1, x2, ⋯, xp, 构成样本矩阵X。

X=x11x12…x1px21x22⋯x2p⋮⋮⋱⋮xn1xn2⋯xnp（5）

（2）数据标准化处理。为消除样本参数量纲及数量级差异的影响, 需对原始数据进行标准化处理。

${{z}_{ij}}=\frac{{{x}_{ij}}-{{{\bar{x}}}_{j}}}{S_{j}^{2}}$（6）

其中: ${{\bar{x}}_{j}}=\frac{\mathop{\sum }_{i=1}^{n}{{x}_{ij}}}{n}$

$S_{j}^{2}=\frac{\mathop{\sum }_{i=1}^{n}{{({{x}_{ij}}-{{{\bar{x}}}_{j}})}^{2}}}{n-1}$

（3）求取标准化后样本矩阵的相关系数矩阵。

R=r11r12⋯r1pr21r22⋯r2p⋮⋮⋱⋮rn1rn2⋯rnp（7）

（4）计算相关系数矩阵的特征值与特征向量。利用雅可比行列式法求解相关系数矩阵的特征方程 R-λE=0的p个非负特征值λ i（λ 1≥ λ 2≥ ⋯≥ λ p> 0）和相对应的正交化单位特征向量[22]。

ai=a1i, a2i, ⋯, aniT（8）

式中：ai为单位特征向量; E为单位矩阵; λ i为矩阵R第i个特征值, 也是主成分Yi的方差, 其值越大, 对总方差的贡献越大。

（5）合理选取k个主成分。首先计算主成分Yi的方差贡献率和累计方差贡献率, 然后选取累计方差贡献率超过85%的k个主成分进行最终分析, 从而筛选出样本参数的主要因子[23, 24]。

3 实例研究
3.1 测井参数敏感性分析

表1总结了研究区112个试气层段不同流体性质致密砂岩储层的测井参数数据, 包括地层真电阻率（RT）、声波时差（AC）、补偿密度（DEN）、补偿中子（CNL）、孔隙度（Por）、渗透率（Perm）、泥质含量（Vsh）、声波时差-补偿中子曲线幅度差（A1）。其中, 泥质含量（Vsh）的计算公式为：

${{V}_{\text{sh}}}=\frac{\ \ \ {{2}^{GCUR\times {{I}_{GR}}}}\ \ \ \ \ \ \ \ -1\ \ \ }{{{2}^{GCUR}}\ \ \ \ \ -1}$（9）

式中：GCUR是希尔奇指数, 其值与地层地质年代相关, 老地层GCUR取2, 新地层GCUR取3.7; IGR为泥质含量指数, 其值等于自然伽马（GR）曲线相对值。

表1 研究区不同流体性质致密砂岩储层测井参数统计

对于纯水层, 当地层孔隙中一部分水被天然气所代替时, 会导致地层含氢指数和密度值减小, 声波时差变大, 甚至发生“ 周波跳跃” , 此类现象被称为“ 挖掘效应” [25]。因此, 声波时差-补偿中子曲线幅度差（A1）可以用来表示储层挖掘效应的强弱, 其值越高, 代表储层含气性越高。对声波时差和补偿中子测井曲线值进行归一化处理, 以消除曲线刻度影响。声波时差-中子曲线幅度差（A1）可通过以下公式计算：

A1=AC* -CNL* （10）

其中:$A{{C}^{\text{*}}}=\frac{A{{C}_{\text{max}}}\ \ \ -\ \ AC}{A{{C}_{\text{max}}}\ \ -\ \ A{{C}_{\text{min}}}}$

$CN{{L}^{\text{*}}}=\frac{CN{{L}_{\text{max}}}\ \ \ -\ \ CNL}{CN{{L}_{\text{max}}}\ \ \ -\ \ CN{{L}_{\text{min}}}}$

式中：AC* 、CNL* 分别为声波时差、补偿中子测井曲线数据的归一化值; max和min分别代表AC、CNL对应数据的最大值和最小值。

以上8个测井参数虽然均能不同程度地反映储层流体性质的变化（表1）, 但对储层流体的敏感性有所区别。若同时选取8个测井参数作为样本数据, 会加大分析过程的复杂程度, 降低测井解释准确性。

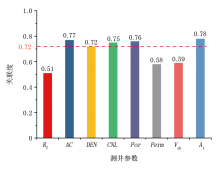
本文基于灰色关联法, 以单层试气产量作为母序列, 试气层测井参数作为子序列, 依次获取了8个测井参数与试气产量的关联系数及关联度, 结果如图2所示。各因素关联度处于0.51~0.78之间, 其排序结果为：A1（0.78）> AC（0.77）> Por（0.76）> CNL（0.75）> DEN（0.72）> Vsh（0.59）> Perm（0.58）> RT（0.51）。本文以灰色关联度为0.72为界, 选取A1、AC、Por、CNL、DEN（灰色关联度≥ 0.72）5个测井参数作为主成分分析的样本数据。

图2 测井参数与试气产量灰色关联度分析结果

3.2 主成分计算

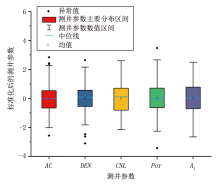
对优选出的测井参数进行主成分分析, 首先需要利用公式（6）对原始测井数据进行标准化处理, 使所有变量的均值为0, 方差为1, 且分布范围一致, 从而消除不同变量间数量级和量纲差异的影响[24], 增强数据之间的可对比性（图3）[26]。然后, 利用标准化后的数据计算样本矩阵对应的相关系数矩阵（表2）。在相关性分析的基础上, 利用雅可比行列式法求解相关系数矩阵的特征方程, 得到特征值和对应的特征向量以及5个主成分（Y1-Y5）的方差贡献率（表3）。

图3 各测井参数标准化后的分布范围

表2 相关系数矩阵
表3 研究区样本参数的特征向量、特征值及方差贡献率

根据特征值及其对应的特征向量的计算结果, 可获得的5个主成分（Y1-Y5）的方程表达式如下：

Y1=0.527AC'-0.543DEN'+0.04CNL'+0.601Por'+0.253A1' （11）

Y2=0.068AC'-0.058DEN'+0.729CNL'+0.121Por'-0.668A1' （12）

Y3=0.716AC'+0.634DEN'+0.174CNL'-0.145Por'+0.182A1' （13）

Y4=-0.17AC'+0.516DEN'-0.299CNL'+0.742Por'-0.254A1' （14）

Y5=-0.418AC'+0.183DEN'+0.589CNL'+0.229Por'+0.626A1' （15）

式中：AC'、DEN'、CNL'、Por'、A1'分别为声波时差、补偿密度、补偿中子、孔隙度和声波时差-中子曲线幅度差样本数据的标准化值。

根据主成分分析原理, 5个主成分（Y1-Y5）相互独立。从分析结果（表3）可以看出, Y1的方差贡献率最大, 达54.57%; Y2的贡献率次之, 为32.42%, Y1和Y2两个主成分的累计方差贡献率超过85%, 说明选用这两个主成分可有效代表原始样本86.99%的信息, 数据信息损失量较小。

3.3 利用主成分识别流体性质

常规交会图法通常只能同时采用2至3项测井参数来进行储层流体性质识别, 评价参数指标数量少, 识别能力较弱, 因此必须增加更多测井参数作为评价指标, 才能有效区分储层流体性质。此外, 常规交会图忽略了测井参数指标之间所反映的信息可能存在一定的重合, 导致彼此之间具有相关性, 这也会增加数据点的重叠, 降低区分度。如图1中RT与AC、DEN、CNL这4项测井参数值一定程度上都受到储层岩石物性、流体类型及饱和度的影响, 所反映的信息重复性和相似性较高, 因此加大了不同流体性质储层数据点间的重叠程度, 导致RT与其他测井参数的交会结果难以有效区分储层流体性质。

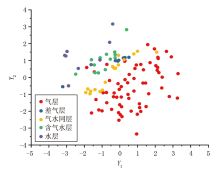
主成分分析法通过将5项原始敏感测井参数高维数据进行正交变换, 将其转换成2个相互独立的主成分变量, 从而实现数据降维的目的。主成分Y1和Y2基本涵盖了5项原始测井变量全部信息且彼此之间互不相关, 有效弥补了常规交会图法的缺陷。通过对主成分Y1和Y2进行交会分析发现（图4）, 储层流体识别能力相对于常规交会图法显著提升。除差气层与部分气水同层数据点发生重叠以外, 其他流体类型储层的数据点之间都存在较为明显的界限, 说明主成分Y1和Y2能够有效突出储层流体性质的变化特征。

图4 主成分Y1、Y2交会图

在主成分分析优化结果的基础上, 利用Fisher判别分析法, 可建立不同流体储层的判别函数来进行定量辅助识别。

F（xi）=aY1+bY2+c （16）

式中：F（xi）为第i种流体类型储层的判别函数; a、b、c分别为判别函数的系数和常数项。

将公式（11）、（12）带入公式（16）中, 即可得到不同流体类型储层的定量判别模型。

气层：F（1）=0.428AC'-0.453DEN'-0.647CNL'+0.446Por'+0.863A1'-2.183 （17）

差气层：F（2）=-0.333AC'+0.363DEN'+0.79CNL'-0.337Por'-0.952A1'-2.236 （18）

气水同层：F（3）=-0.274AC'+0.287DEN'+0.298CNL'-0.293Por'-0.441A1'-1.793 （19）

含气水层：F（4）=-0.625AC'+0.659DEN'+1.11CNL'-0.643Por'-1.42A1'-3.067 （20）

水层：F（5）=-1.241AC'+1.307DEN'+1.674CNL'-1.308Por'-2.307A1'-5.961 （21）

通过对研究区储层段气层、差气层、气水同层、含气水层、水层112个试气层样本数据的识别结果进行回判统计, 结果见表4。

表4 新方法的储层流体性质解释结果

其中, 正判个数共计97个, 整体符合率为86.6%, 气层判别符合率达到92.3%, 表明该方法能有效提高气水层识别精度。

4 应用效果
4.1 S 20-17-5井

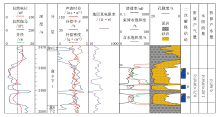
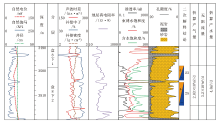
研究区S 20-17-5井盒8段试气3段, 平均无阻流量为1.02× 104 m3/d, 产气为0.71× 104 m3/d, 产水为6.4 m3/d。6#、8#、10#储层段测井曲线均表现出良好的响应特征, 即电阻率增高、声波时差增大、补偿中子和补偿密度减小, 利用常规测井交会图板均解释为气层。基于本次研究提出的气水定量判别模型, 对6#、8#、10#储层段进行二次精细解释。根据最大相似性原则, 将待判断储层段测井参数标准化值带入储层流体性质的定量判别公式（17）-（21）中, 计算结果越大, 代表储层流体性质与主成分分析中已知流体性质类型的相似性越强, 即判别方程计算结果最大者对应的流体性质类型即为判别结果。3层二次解释结论为含气水层。该井试气结果显示, 二次解释结论与试气结论一致（图5）。

图5 S 20-17-5井盒8段储层测井解释成果

4.2 S 20-16-1井

研究区S 20-16-1井盒8段试气两段, 平均无阻流量为3.2× 104 m3/d, 产气为2.03× 104 m3/d, 产水为4.8 m3/d。其中, 23#砂体深度3 498.0~3 503.9 m, 地层电阻率偏高, 平均值为91.2 Ω ∙ m, 声波时差221.8 μ s/m, 补偿中子5.95%, 补偿密度2.52 g/cm3, 利用常规测井交会图板解释为气层; 25#砂体深度3 504.7~3 514.2 m, 地层电阻率上部高、下部低, 平均值为65.8 Ω ∙ m, 声波时差218.8 μ s/m, 补偿中子7.35%, 补偿密度2.52 g/cm3, 利用常规测井交会图板解释为气水同层。基于本次研究提出的气水定量判别模型, 对23#、25#砂体进行二次解释。两层二次解释结论均为气水同层, 与试气结论一致, 表明该方法相比常规交会图法对于识别研究区气水层的精度更高（图6）。

图6 S 20-16-1井盒8段储层测井解释成果

5 结论

（1）研究区储层气水关系复杂, 流体测井响应特征不明显, 高、低阻气、水层并存, 利用常规测井交会图法识别储层流体性质的解释符合率低, 难以满足现场生产需求。

（2）利用灰色关联法优选出对储层流体性质变化敏感性最强的声波时差（AC）、补偿密度（DEN）、补偿中子（CNL）、孔隙度（Por）和声波时差-补偿中子曲线幅度差（A1）, 对这5种测井响应参数进行主成分分析, 提取累计方差贡献率为86.99%的主成分Y1和Y2, 并结合Fisher判别分析法, 建立了不同流体性质储层定量解释模型。该模型整体解释符合率为86.6%, 气层解释符合率为92.3%。

（3）相对于常规交会图法, 该方法综合了更多测井曲线信息对储层流体性质进行识别, 同时也避免了测井参数之间相关性导致的多解性, 在研究区储层流体性质识别方面具有较高的解释精度, 实用性更强。

编辑 孔宪青

参考文献
[1] 贾爱林, 位云生, 郭智, 等. 中国致密砂岩气开发现状与前景展望[J]. 天然气工业, 2022, 42(1): 83-92.
JIA Ailin, WEI Yunsheng, GUO Zhi, et al. Development status and prospect of tight sand stone gas in China[J]. Natural Gas Industry, 2022, 42(1): 83-92. [本文引用:1]
[2] 何东博, 贾爱林, 冀光, 等. 苏里格大型致密砂岩气田开发井型井网技术[J]. 石油勘探与开发, 2013, 40(1): 79-89.
HE Dongbo, JIA Ailin, JI Guang, et al. Well type and pattern optimization technology for large scale tight sand gas, Sulige Gas field[J]. Petroleum Exploration and Development, 2013, 40(1): 79-89. [本文引用:1]
[3] 杨华, 付金华, 刘新社, 等. 苏里格大型致密砂岩气藏形成条件及勘探技术[J]. 石油学报, 2012, 33(增刊1): 27-36.
YANG Hua, FU Jinhua, LIU Xinshe, et al. Formation conditions and exploration technology of large-scale tight sand stone gas reservoir in Sulige[J]. Acta Petrolei Sinica, 2012, 33(S1): 27-36. [本文引用:1]
[4] 卢涛, 刘艳侠, 武力超, 等. 鄂尔多斯盆地苏里格气田致密砂岩气藏稳产难点与对策[J]. 天然气工业, 2015, 35(6): 43-52.
LU Tao, LIU Yanxia, WU Lichao, et al. Challenges to and countermeasures for the production stabilization of tight sand stone gas reservoirs of the Sulige Gasfield, Ordos Basin[J]. Natural Gas Industry, 2015, 35(6): 43-52. [本文引用:1]
[5] 王继平, 张城玮, 李建阳, 等. 苏里格气田致密砂岩气藏开发认识与稳产建议[J]. 天然气工业, 2021, 41(2): 100-110.
WANG Jiping, ZHANG Chengwei, LI Jianyang, et al. Tight sand stone gas reservoirs in the Sulige Gasfield: Development understand ings and stable-production proposals[J]. Natural Gas Industry, 2021, 41(2): 100-110. [本文引用:1]
[6] 程立华, 郭智, 孟德伟, 等. 鄂尔多斯盆地低渗透-致密气藏储量分类及开发对策[J]. 天然气工业, 2020, 40(3): 65-73.
CHENG Lihua, GUO Zhi, MENG Dewei, et al. Reserves grading classification and development countermeasures for low-permeability tight gas reservoirs in the Ordos Basin[J]. Natural Gas Industry, 2020, 40(3): 65-73. [本文引用:1]
[7] 光友会, 张子为, 彭述兴, 等. 低阻致密气藏多学科融合气水解释评价技术[J]. 断块油气田, 2022, 29(4): 508-513.
GUANG Youhui, ZHANG Ziwei, PENG Shuxing, et al. Multidisciplinary integrated gas-water interpretation and evaluation technology for low-resistance tight gas reservoirs[J]. Fault-Block Oil and Gas Field, 2022, 29(4): 508-513. [本文引用:1]
[8] 王安龙. 基于常规测井资料综合评价延川南致密砂岩气层[J]. 油气藏评价与开发, 2019, 9(2): 75-79, 82.
WANG Anlong. Comprehensive evaluation of dense sand stone gas layer in southern Yanchuan area based on conventional logging data[J]. Reservoir Evaluation and Development, 2019, 9(2): 75-79, 82. [本文引用:1]
[9] 冯春珍, 邵德艳, 胡晓丽, 等. 苏里格气田W区盒8段储层特征与快速气水识别方法[J]. 测井技术, 2014, 38(5): 558-563.
FENG Chunzhen, SHAO Deyan, HU Xiaoli, et al. Reservoir characteristics and rapid gas-water identification method of He 8 Member in Block W of Sulige Gasfield[J]. Well Logging Technology, 2014, 38(5): 558-563. [本文引用:1]
[10] 刘毅, 李建奇, 冯强汉, 等. 苏里格气田苏48区块石盒子组8段气水识别方法研究[J]. 石油天然气学报(江汉石油学院学报), 2014, 36(9): 84-87.
LIU Yi, LI Jianqi, FENG Qianghan, et al. Research on gas-water identification method in Member 8 of Shihezi Formation in Block Su 48 of Sulige Gasfield[J]. Journal of Oil and Gas Technology (J. JPI), 2014, 36(9): 84-87. [本文引用:1]
[11] 李昌绵, 李爽, 柳琳, 等. 苏里格气田苏S区块高含水气藏气水识别及开发对策研究[J]. 非常规油气, 2022, 9(3): 64-71.
LI Changmian, LI Shuang, LIU Lin, et al. Study on gas-water identification and development strategy of high water-cut gas reservoir in Su S block of Sulige Gasfield[J]. Unconventional Oil & Gas, 2022, 9(3): 64-71. [本文引用:1]
[12] 付斌, 李进步, 陈龙, 等. 苏里格气田西区致密砂岩气水识别方法与应用[J]. 特种油气藏, 2014, 21(3): 66-69.
FU Bin, LI Jinbu, CHEN Long, et al. Gas and water identification method and application in tight sand stone in the western region of Sulige GasField[J]. Special Oil & Gas Reservoirs, 2014, 21(3): 66-69. [本文引用:1]
[13] 李霞, 石玉江, 王玲, 等. 致密砂岩气层测井识别与评价技术: 以苏里格气田为例[J]. 天然气地球科学, 2013, 24(1): 62-68.
LI Xia, SHI Yujiang, WANG Ling, et al. Logging identification and evaluation technology for tight sand stone gas zones: Taking Sulige Gasfield as an example[J]. Natural Gas Geoscience, 2013, 24(1): 62-68. [本文引用:1]
[14] HUANG B Z, PAN B Z. Characteristics of log responses and lithology determination of igneous rock reservoirs[J]. Journal of Geophysics and Engineering, 2004, 1(1): 51-55. [本文引用:1]
[15] 苟启洋, 徐尚, 郝芳, 等. 基于灰色关联的页岩储层含气性综合评价因子及应用: 以四川盆地焦石坝区块为例[J]. 天然气地球科学, 2019, 30(7): 1045-1052.
GOU Qiyang, XU Shang, HAO Fang, et al. A comprehensive evaluation index of gas-bearing property of shale reservoirs based on grey relation and its application: Case study of Jiaoshiba area, Sichuan Basin[J]. Natural Gas Geoscience, 2019, 30(7): 1045-1052. [本文引用:1]
[16] 刘凤伟, 谢传礼, 刘超, 等. 基于灰色关联分析法的致密油储层定量评价[J]. 地质科技情报, 2016, 35(5): 168-175.
LIU Fengwei, XIE Chuanli, LIU Chao, et al. Quantitative evaluation of tight oil reservoirs based on grey relational analysis[J]. Bulletin of Geological Science and Technology, 2016, 35(5): 168-175. [本文引用:1]
[17] 方辉煌, 汪吉林, 宫云鹏, 等. 基于灰色模糊理论的页岩气储层评价: 以重庆南川地区龙马溪组页岩为例[J]. 岩性油气藏, 2016, 28(5): 76-81.
FANG Huihuang, WANG Jilin, GONG Yunpeng, et al. Evaluation of shale gas reservoirs based on gray fuzzy theory: A case study from Longmaxi Formation in Nanchuan area, Chongqing[J]. Lithologic Reservoirs, 2016, 28(5): 76-81. [本文引用:1]
[18] 朱兆群, 林承焰, 张苏杰, 等. 改进的模糊-灰色综合评判方法在储层定量评价中的应用: 以苏里格气田苏X井区盒8下亚段低渗透气藏为例[J]. 石油与天然气地质, 2017, 38(1): 197-208.
ZHU Zhaoqun, LIN Chengyan, ZHANG Sujie, et al. Application of improved fuzzy-grey comprehensive evaluation method to quantitative reservoir evaluation: A case study of the low-permeability gas reservoirs of the lower part of 8th member of the Shihezi Formation in Su X block of Sulige Gasfield[J]. Oil & Gas Geology, 2017, 38(1): 197-208. [本文引用:1]
[19] 叶涛, 韦阿娟, 黄志, 等. 基于主成分分析法与Bayes判别法组合应用的火山岩岩性定量识别: 以渤海海域中生界为例[J]. 吉林大学学报(地球科学版), 2019, 49(3): 872-879.
YE Tao, WEI Ajuan, HUANG Zhi, et al. Quantitative identification of volcanic rock lithology based on the combination of principal component analysis and Bayes discriminant method: Taking the Mesozoic in the Bohai Sea as an example[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(3): 872-879. [本文引用:1]
[20] 张强, 李家金, 王毛毛, 等. 基于改进主成分分析法的测井曲线岩性分层技术[J]. 吉林大学学报(地球科学版), 2022, 52(4): 1369-1376.
ZHANG Qiang, LI Jiajin, WANG Maomao, et al. Logging curve rock layering technology based on improved principal component analysis[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(4): 1369-1376. [本文引用:1]
[21] 高阳, 李忠新. 基于主成分分析的致密砂砾岩孔隙度测井评价方法[J]. 沉积学报, 2016, 34(4): 716-724.
GAO Yang, LI Zhongxin. Logging interpretation of porosity for tight glutenite based on principal component analysis[J]. Acta Sedimentologica Sinica, 2016, 34(4): 716-724. [本文引用:1]
[22] 刘毅, 陆正元, 吕晶, 等. 主成分分析法在泥页岩地层岩性识别中的应用[J]. 断块油气田, 2017, 24(3): 360-363.
LIU Yi, LU Zhengyuan, LYU Jing, et al. Application of principal component analysis method in lithology identification for shale formation[J]. Fault-Block Oil & Gas Field, 2017, 24(3): 360-363. [本文引用:1]
[23] 杨兆栓, 林畅松, 尹宏, 等. 主成分分析在塔中地区奥陶系鹰山组碳酸盐岩岩性识别中的应用[J]. 天然气地球科学, 2015, 26(1): 54-59.
YANG Zhaoshuan, LIN Changsong, YIN Hong, et al. Application of principal component analysis in carbonate lithology identification of the Ordovician Yingshan Formation in Tazhong area[J]. Natural Gas Geoscience, 2015, 26(1): 54-59. [本文引用:1]
[24] 刘爱疆, 左烈, 李景景, 等. 主成分分析法在碳酸盐岩岩性识别中的应用: 以YH地区寒武系碳酸盐岩储层为例[J]. 石油与天然气地质, 2013, 34(2): 192-196.
LIU Aijiang, ZUO Lie, LI Jingjing, et al. Application of principal component analysis in carbonate lithology identification: A case study of the Cambrian carbonate reservoir in YH area[J]. Oil & Gas Geology, 2013, 34(2): 192-196. [本文引用:2]
[25] 张志虎, 孙玉红, 金力钻, 等. 致密砂岩气层测井评价新方法研究[J]. 特种油气藏, 2015, 22(5): 46-49.
ZHANG Zhihu, SUN Yuhong, JIN Lizuan, et al. Research on new logging evaluation methods for tight sand stone gas zones[J]. Special Oil & Gas Reservoirs, 2015, 22(5): 46-49. [本文引用:1]
[26] 尹帅, 丁文龙, 汤婕, 等. 主成分分析法在致密碎屑岩储层有效裂缝识别中的应用[J]. 油气地质与采收率, 2016, 23(6): 1-7.
YIN Shuai, DING Wenlong, TANG Jie, et al. Application of principal component analysis method to effective fracture identification of tight clastic rock reservoir[J]. Petroleum Geology and Recovery Efficiency, 2016, 23(6): 1-7. [本文引用:1]