引用本文
孙婧, 赵军龙, 刘军锋. 基于Lasso-SSA-Adaboost组合模型的致密砂岩储层岩性识别[J]. 录井工程, 2025,36(1): 41-48.
SUN Jing, ZHAO Junlong, LIU Junfeng. Lithology identification of tight sandstone reservoirs based on Lasso-SSA-Adaboost combined model[J]. Mud Logging Engineering, 2025,36(1): 41-48.
Doi:10.3969/j.issn.1672-9803.2025.01.007  
Permissions
Copyright©2025, 《录井工程》杂志社
《录井工程》杂志社 所有
基于Lasso-SSA-Adaboost组合模型的致密砂岩储层岩性识别
孙婧①,②, 赵军龙①,②, 刘军锋③
①西安石油大学地球科学与工程学院
②陕西省油气成藏地质学重点实验室
③中国石油长庆油田公司第二采油厂
通讯作者：赵军龙 1970年生,博士,教授,从事测井资料处理与解释、复杂油气藏测井评价研究工作。E-mail：zjl1970@163.com

作者简介：孙婧 1998年生,西安石油大学在读研究生,从事测井地质综合研究、测井资料处理与解释工作。通信地址：710000 陕西省西安市雁塔区电子二路东段18号西安石油大学雁塔校区。E-mail：19801360170@163.com

收稿日期: 2024-10-17
基金: 陕西省自然科学基础研究计划（编号：2019JM-359）
摘要

为了提高利用测井资料识别致密砂岩储层岩性的精度和效率,基于文献调研,提出Lasso-SSA-Adaboost组合模型识别致密砂岩储层岩性。首先采用最小绝对收缩和选择算子（Lasso）模型对原始数据集特征值重要性进行排序及特征降维,进而把对于岩性识别分类精度更高的特征值送入自适应提升算法（Adaboost）模型进行训练学习;由于Adaboost在建模过程中使用较多超参数,因此采用麻雀优化搜索算法（SSA）对其进行超参寻优以获得最佳参数组合。以J研究区延8段致密砂岩储层测井及岩心数据为基础,训练构建Lasso-SSA-Adaboost组合模型。经Lasso模型特征提取后,Adaboost模型迭代误差率较未使用Lasso算法明显降低,岩性识别准确率提升明显;SSA算法全局优化搜索经较少次数迭代获得Adaboost最优超参数,提升了模型训练精度及效率。与K-近邻算法（KNN）模型和随机森林模型识别岩性效果进行对比,Lasso-SSA-Adaboost组合模型在测试集上预测准确率达到90%以上,表明了其在研究区应用效果较好。

关键词: 致密砂岩储层; 岩性识别; Lasso; SSA; Adaboost; 组合模型
中图分类号:TE132.1 文献标志码:A
Lithology identification of tight sandstone reservoirs based on Lasso-SSA-Adaboost combined model
SUN Jing①,②, ZHAO Junlong①,②, LIU Junfeng③
①School of Earth Sciences and Engineering of Xi′an Shiyou University,Xi′an,Shaanxi 710000,China
②Shaanxi Key Laboratory of Petroleum Accumulation Geology,Xi′an,Shaanxi 710000,China
③NO.2 Oil Production Plant,Qingdao,Gansu 745100,China
Abstract

In order to improve the accuracy and efficiency of using well-log information to identify the lithology of tight sandstone reservoirs,based on literature researches,a Lasso-SSA-Adaboost combined model is proposed to identify the lithology of tight sandstone reservoirs. First,the Least Absolute Shrinkage and Selection Operator（Lasso） model is used to order the importance of the original data set ′s eigenvalues and reduce feature dimensionality. Then,the eigenvalues with higher accuracy for lithology identification and classification are fed into the Adaptive Boosting（Adaboost） model for training and learning. Due to the frequent use of hyperparameters in the modeling process of Adaboost,the Sparrow Search Algorithm（SSA） is adopted to perform hyperparameter optimization to obtain the optimal combination of parameters. Based on the log and core data of the Yan 8 tight sandstone reservoirs in the J study area,a Lasso-SSA-Adaboost combined model was trained and constructed, and compared the effects of identifying lithology with K-nearest neighbor（KNN） algorithm and random forest model. After feature extraction using the Lasso model,the iteration error rate of the Adaboost model is significantly reduced compared to not using the Lasso algorithm,and the accuracy of lithology identification is significantly improved. The global optimization search of SSA algorithm obtains the optimal hyperparameters of Adaboost through fewer iterations,which improves the training accuracy and efficiency of the model. The prediction accuracy of Lasso-SSA-Adaboost combined model is over 90% on the test set,showing its good effects in the study area.

Keyword: tight sandstone reservoir; lithology identification; Lasso; SSA; Adaboost; combined model
0 引言

准确判别储层岩性是油气勘探开发过程中必不可少的一项基础工作, 对于地层划分对比、沉积展布分析、油气储层物性参数求取、含油气性评价、地质建模、油藏描述等方面的地质工作开展至关重要[1, 2, 3]。利用测井资料进行岩性识别, 具备效率高、成本效益好等优势, 目前被广泛使用。测井资料识别岩性主要通过交会图法[4]、统计学法[5]以及成像测井[6, 7], 但对于非常规油气藏如致密砂岩储层, 其沉积环境与岩性成分均复杂多样、不同岩性的测井响应相似度高, 在传统交会图板上难以清晰有效辨别[3]。由于致密砂岩储层非均质性影响, 测井响应与实际油气储层岩性之间呈现非线性关系, 采用线性测井响应方程和统计经验公式难以表征储层岩性真实特性, 导致其结果主观性及不确定性增加。此外, 层析成像测井价格昂贵, 不利于广泛实际使用[1]。

机器学习能高效挖掘测井数据与岩性之间多维度非线性映射关系, 利于实现高精度、高效率自动识别, 为岩性识别领域提供了新思路。目前, 岩性识别领域常使用的机器学习算法有：支持向量机（SVM）、BP神经网络、梯度提升决策树、K-近邻算法（KNN）等。较于传统的支持向量机等方法, 结合优化算法优化向量机参数改进传统支持向量机可以大幅提高岩性识别效率。林香亮等[8]提出主成分分析与支持向量机结合PCA-SVM模型可有效提高砂砾岩岩性识别效率; 苏赋等[9]将模糊隶属度函数与孪生支持向量机结合, 在复杂岩性识别中取得了较佳识别效果; 李曦等[10]提出粒子群优化支持向量机参数PSO-SVM模型, 岩性识别效率达97%; 张晗等[11]将BP神经网络应用于复杂岩性致密层, 岩性预测结果与实际目标岩性基本吻合; 武中原等[12]利用循环神经网络（LSTM）实现测井序列与岩性序列垂向匹配, 岩性识别提升效果明显; 刘跃杰等[13]基于主成分分析优选对测井相划分贡献较大的主成分, 并结合BP神经网络使得页岩岩相识别准确率得到有效提高; 韩启迪等[14]基于梯度提升决策树（GBDT）对覆盖区下伏岩体进行有效岩性识别, 验证了与单一学习器相比, 基于多个学习器的GBDT模型具有更高的预测精度; 刘凯等[15]利用随机森林模型开展火成岩岩性智能解释, 结果表明, 智能模型预测结果与井段取心高度符合; 彭英等[16]提出基于FL-XGBoost模型的砂泥岩识别方法, 取得了较佳识别效果, 解决了胜利油田砂泥岩识别关键技术难点; 赵彤彤等[17]基于KNN模型开展岩性识别研究, 取得了较好的识别效果; 张梓童等[18]验证了KNN模型可以作为一种岩性识别研究有效手段; 陈玉林等[19]验证了KNN算法对于复杂储层岩相识别应用效果显著。

以上算法有效性在许多应用实例中均得到充分肯定, 但也忽视了以下问题：SVM处理高维大规模数据需要大量内存及计算时间, 在高维空间中计算复杂度会增加; BP神经网络采用局部最优搜索来解决优化问题, 训练过程局部最优非全局最优导致模型应用于新数据集泛化性不佳; KNN易将样本预测偏向于学习样本数据规模较多的类别; LSTM在分类任务中存在计算效率低（无法并行处理长序列）、长距离依赖捕捉能力有限, 以及参数量大易过拟合的问题; GBDT对于异常值更敏感（因直接拟合残差）, 且单轮迭代需串行生成多棵决策树, 计算效率较低; 一般采用的优化算法如粒子群优化算法（PSO）性能高度依赖于参数选择, 不同参数设置可能会导致算法收敛速度慢或陷入局部最优解。

Adaboost作为集成学习算法这类优秀模式识别技术的代表之一, 能逐步提高错分样本权重, 起到了正则化效果, 且通过限制弱分类器复杂度, 可减少过拟合, 融入并行化处理从而提高计算效率; 自适应调整机制使得每轮迭代根据上一轮分类情况调整权重, 对于各类型数据表现出较强适应性[20, 21, 22]。Adaboost模型在建模过程中还存在以下不足：建模需要较多经验超参数参与, 模型状态难以保持最优; 当特征维度变高时, 为提高模型训练效率, 其通过自身随机变量采样技术实现, 但这种随机处理方式易使模型建模后状态难以确保最优。

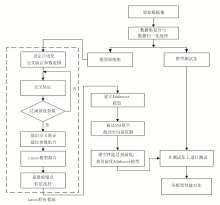
为了使Adaboost模型在建模后状态达到最佳, 本文采用最小绝对收缩和选择算子（Lasso）模型和麻雀优化搜索算法（SSA）模型对其进行改进。Lasso模型具有特征提取功能, 能从源数据中依据特征重要性排序, 提取对于预测分类问题更高效的特征值, 从而解决高维数据特征带来的影响; 而SSA模型能有效解决参数优化问题。为此, 本文提出构建Lasso-SSA-Adaboost组合模型来解决研究区储层岩性识别问题。

1 相关算法原理
1.1 Lasso算法

Lasso算法是一种应用于模型特征选择的正则化方法。

Lasso基本思想是通过在线性回归的损失函数中添加一个L1正则化项, 即系数绝对值之和, 以限制回归系数的大小, 该约束使得一些不重要的特征系数变为零, 而对模型预测有利的系数将会保留, 从而实现特征选择。具体公式如下。

在标准线性回归中, 模型损失函数是最小化残差平方和（RSS）：

RSS=∑i=1n（yi-β0-∑j=1pxijβj）2（1）

Lasso回归在此基础上引入了L1正则化项, 损失函数f（x）变为：

f（x）=min∑i=1n（yi-β0-∑j=1pxijβj）2+λ∑j=1p|βj|（2）

式中： yi为目标变量的实际值（其中 i=1，2，…，n, n为样本总数）; xij为第 i个样本的第 j个特征的值（其中 j=1，2，…，p，j表示特征索引, p为特征总数）; β0为截距项, 表示模型在所有特征都为0时的预测值; βj为第j个特征的系数, 表示该特征对于目标变量的影响程度; λ为正则化系数, 用于平衡模型的拟合优度及复杂度, 防止过拟合; ∑j=1p|βj|为L1范式, 表示模型系数绝对值之和。

L1正则化项引入使得优化过程不仅考虑拟合数据优度, 还考虑模型参数大小。

1.2 SSA算法

SSA算法是由Xue等[23]基于麻雀觅食行为提出的一种启发式群优化算法, 主要模拟该过程中探索者、追随者和警戒者3种角色各自行为, 通过三者协作来解决复杂优化问题。

SSA基本原理如下：

（1）探索者行为：在全局大范围搜索, 以发现潜在的高质量解, 负责为种群提供全局解决方案。在每轮迭代中, 探索者位置更新规则主要与两个因素有关：一是预警值（ r2）, 表示环境中危险程度; 二是安全阈值 （ST）, 表示麻雀的警戒状态。当 r2< ST时, 探索者进行大范围的跳跃搜索; 当 r2≥ ST时, 探索者会寻找其他区域进行搜索。

（2）追随者行为：依据探索者搜索指引, 在探索者发现区域内进行局部搜索, 以寻求更加优质解。追随者位置更新取决于其适应度（即当前解质量）。若某只追随者的适应度较差, 其会进行跳跃式搜索, 以摆脱不良解位置, 向更优解方向移动; 否则, 会在探索者发现的最优位置附近进行微调和搜索, 以进一步优化解。

（3）警戒者行为：警戒者为种群中部分麻雀, 通常由探索者与追随者中随机挑选出来, 负责监视环境中的危险, 并采取策略避免种群陷入局部最优解。

1.3 Adaboost算法

Adaboost算法是一种基于弱学习器的自适应提升算法, 基于弱学习器线性组合中构建的一个强分类器[24]。

Adaboost算法核心原理如下：

（1）训练弱分类器：在每一轮迭代中, Adaboost模型会基于当前的样本权重分布训练一个弱分类器。弱分类器通常是简单且性能有限的模型（如决策树桩、朴素贝叶斯分类器、支持向量机等）。

（2）样本权重分配：在初始时, 所有样本所分配的权重相等。Adaboost在每一轮训练时, 会根据上一轮迭代中错误分类的样本来调整样本权重, 正确分类的样本权重减小, 被错误分类的样本权重增加, 使得这些样本在下一轮训练中受到更多关注。

（3）组合弱分类器：Adaboost根据每个弱分类器的错误率计算其权重。错误率越低的弱分类器, 权重越高, 最终的强分类器是这些弱分类器的加权组合。在做出决策时, Adaboost会综合所有弱分类器的结果进行加权投票或求和, 得到最终预测结果。

2 实例验证
2.1 实验数据及建模流程

2.1.1 实验数据来源及预处理

本文以J研究区延8段致密砂岩储层为研究对象。根据岩心测试资料, 识别出目的层主要岩性共有5种, 分别为细砂岩、粗砂岩、中砂岩、泥质粉砂岩、泥岩, 本文规定各岩性对应原始编码依次为数字1~5。样本由测井曲线和岩心信息组成, 组成训练及测试样本共569组, 其中, 1-细砂岩数据133组、2-粗砂岩数据93组、3-中砂岩数据112组、4-泥质粉砂岩数据107组、5-泥岩数据124组。模型原始输入测井曲线有11条, 分别为自然电位（SP）、自然伽马（GR）、声波时差（AC）、原状地层电阻率（RT）、补偿中子（CNL）、补偿密度（DEN）、阵列感应电阻率（AT10、AT20、AT30、AT60）、光电效应截面指数（Pe）。在本次研究中, 由于不同测井响应之间属性值差异过大对预测结果造成影响, 在进行实验之前, 采用归一化处理对测井曲线数据集进行预处理。某类岩性测井参数归一化计算公式如下：

Xkm'=Xkm-min（Xkm）max（Xkm）-min（Xkm）（3）

式中： Xkm'为归一化后的后第k类测井参数的第m个数据值（k=1, 2, …, 11）; Xkm为第k类测井参数的第m个实际值; min（Xkm）为第k类测井参数最小值; max（Xkm）为第k类测井参数最大值。

2.1.2 Lasso-SSA-Adaboost组合模型构建

本次实验代码程序以及建模测试环境为64位Windows 10操作系统, 软件操作平台为Jupyter Notebook, 实验使用的编程开发语言为Python 3.8。对于归一化之后的训练数据, 设置网格搜索Lasso算法主要参数正则化系数（ λ）的范围值分别为0.001、0.01、0.1、1.0、10, 并设定交叉验证预设折数为10折进行交叉运算, 迭代次数达到预设折数时, 输出的交叉验证最佳参数组合将作为Lasso模型设定参数组合, 完成模型拟合并观察系数大小及非零项, 从而进行特征重要性排序。经Lasso模型处理得到的特征变量将作为Adaboost模型输入特征, 并开始进行模型特征学习训练。SSA模型通过设置麻雀种群预设值以及迭代次数预设值, 比Adaboost模型更容易找到一组理想设置参数。SSA模型通过不断迭代计算, 更新模型适应度以确保适应度最佳, 获取模型每轮迭代超参数组合不断进行调优, 以确保Adaboost模型预测结果达到最优, 预测识别结果可靠。具体的Lasso-SSA-Adaboost组合模型岩性识别流程如图1所示。

图1 Lasso-SSA-Adaboost组合模型岩性识别流程

2.2 实验过程及分析

2.2.1 评价指标

混淆矩阵可直观衡量分类模型的性能, 统计不同类别样本的分类情况[25]。其中, 行代表分类算法的预测类别, 列代表样本的真实类别, 一般将多数类定义为负类, 少数类定义为正类。其中正类样本预测结果为正类表示为真正例, 负类样本预测结果为正类表示为假正例; 正类样本预测结果为负类表示为假反例, 负类样本预测结果为负类表示为真反例[28]。由此可以引出一些常用指标, 如准确率（A）、精准度（P）、召回率（R）、F1值（F1-score）来检验模型分类性能。具体计算公式如下：

A=TP+TNTP+TN+FP+FN（4）

P=TPTP+FP（5）

R=TPTP+FN（6）

F1=2RPR+P（7）

式中：TP、TN、FP、FN分别为真正例、真反例、假正例、假反例的样本数量。

2.2.2 基于Lasso模型特征重要性排序

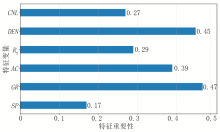
由图2可知, 基于Lasso模型的特征重要性得分由高至低依次为GR、DEN、AC、RT、CNL、SP。其中, GR、DEN、AC特征重要性得分排在前3位, 对本次岩性识别效果显著, 对原始高维特征提取有效。Lasso模型提供的重要特征进行训练建模时, 在训练集上的迭代误差较使用全部测井响应迭代误差低。因此, 剔除一些重要性得分较低的特征, 可在最大限度保持分类精度的同时, 缩减数据规模, 提高岩性识别效果。

图2 基于Lasso模型特征重要性排序

2.2.3 基于SSA模型参数优化

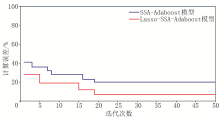
利用归一化后的原始学习样本和Lasso模型提供的重要特征分别对Adaboost模型进行训练。SSA-Adaboost模型及Lasso-SSA-Adaboost模型在训练建模过程中误差随迭代过程收敛如图3所示, 经Lasso模型特征提取后, Adaboost模型迭代误差率较未使用Lasso算法明显降低, SSA模型能够有效地优化Adaboost模型, 特别是在Lasso模型处理重要特征数据的条件下。SSA算法在前5次迭代过程中, 误差收敛速度较快, 而第6次至第15次迭代中, 误差收敛明显降低且接近平缓。主要原因为SSA算法通过全局搜索优化Adaboost模型, 在每一轮迭代中不断更新种群麻雀个体最佳适应度以寻找最佳参数组合, 使模型整体陷入了局部最优解, 模型误差收敛性能降低; 在第16次至第19次迭代过程中误差率又再次降低, 这说明SSA模型已找到全局超参数优化最佳组合, 使得模型较快跳出局部最优解; 第20次迭代之后, 模型训练误差率稳定且不再发生变化, 表明此时模型整体性能已经达到最优, 预测性能达到最好。这也验证了SSA算法在Adaboost模型训练过程中, 具备较好的全局搜索能力, 使得Adaboost模型能够在迭代初期快速完成误差收敛, 在迭代中期也能使Adaboost模型较快跳出局部最优解, 在保证优化效率高的同时提升模型预测精度, 使得模型整体预测性能达到最优。

图3 SSA-Adaboost和Lasso-SSA-Adaboost模型训练误差

在完成Adaboost模型以及Lasso-SSA-Adaboost模型训练之后, 使用测试集进行验证。两种模型在测试集上准确率混淆矩阵结果如图4所示。由图4a可以看出, Adaboost模型在未采用Lasso算法进行重要特征筛选并且模型超参数采用传统经验参数完成建模后, 模型在测试集上整体预测准确率为78.96%, 对于各类岩性预测准确率均较低, 其中对于粗砂岩及泥质粉砂岩预测效果不佳, 两者准确率分别为71.42%和74.03%, 中砂岩岩性识别准确率最高, 也仅为83.77%, 表明模型整体预测效果均不理想, 岩性识别可信度较低。由图4b可以看出, 经过Lasso算法进行重要特征筛选处理以及SSA全局优化搜索找到全局范围最优解组合带入模型完成训练后, 模型对于各类岩性特征区分度敏感性增强, Adaboost模型整体预测准确率从78.96%提升至91.50%, 提升尤为明显; 相较于前者, Lasso-SSA-Adaboost模型对于粗砂岩及泥质粉砂岩预测准确率均有较大提升, 分别为91.32%和89.91%; Lasso-SSA-Adaboost模型对于其他类别岩性预测效果均较好, 对于细砂岩、中砂岩、泥岩的预测准确率分别为90.93%、92.34%、93.17%, 在测试集上的准确率均在90%以上, 达到较好的效果, 说明Lasso-SSA-Adaboost模型整体泛化性以及鲁棒性较好。这表明, 使用Lasso算法及SSA算法对Adaboost模型优化改进效果明显, 整体准确率提升12.54%, 岩性识别效果明显, 模型预测可信度较高。

图4 Adaboost模型及Lasso-SSA-Adaboost模型在测试集上准确率混淆矩阵结果

2.2.4 不同模型预测结果对比

在验证了Lasso算法和SSA算法对Adaboost模型岩性预测能力有较为明显提升作用后, 引入传统分类模型（如KNN模型、随机森林模型）与本文所提出的改进Adaboost模型进行模型性能对比。为了确保所有验证模型在预测时整体性能达到最佳状态, 也将利用Lasso算法和SSA算法对KNN模型以及随机森林模型进行相同条件下的优化处理。表1记录了使用3种优化模型在测试集上的岩性预测结果, 结果显示, 在采用相同优化算法下, Lasso-SSA-Adaboost模型准确率、召回率和F1值分别为91.50%、91.21%和90.52%, 均高于其他两种优化模型, 成为最佳预测模型。图5以岩性柱状图形式展示测试集部分预测结果, 通过观察发现, Lasso-SSA-KNN模型预测结果明显存在多处预测错误样点, Lasso-SSA-随机森林模型略好, 两者预测效果均不理想, Lasso-SSA-Adaboost模型较Lasso-SSA-KNN模型以及Lasso-SSA-随机森林模型得到的预测准确率提升明显, 分类结果可靠。

图5 测试集部分岩性预测柱状图

表1 3种优化模型在测试集上的岩性预测结果对比
3 结论

（1）为提高测井资料对研究区致密砂岩储层岩性识别精度和效率, 本文提出了Lasso-SSA-Adaboost组合模型。通过采用交叉验证设置Lasso算法主参数正则化系数, 模型在迭代过程完成拟合, 并根据系数大小及非零项进行特征重要性排序, 将经Lasso算法所筛选出的特征变量以及设定岩性标签值作为Adaboost建模输入特征集以及标签值, 利用SSA算法不断更新Adaboost模型适应度以确保达到最佳, 从而寻找到Adaboost超参最优组合, 完成Lasso-SSA-Adaboost组合模型建模流程。

（2）实验分析表明, Lasso算法能够从源数据中提取利于建立自变量与因变量映射关系的重要特征, 为提高Adaboost算法效率奠定特征维度基础; SSA算法在Adaboost训练过程中, 具备较好的全局搜索能力, 使得Adaboost模型在迭代过程中快速完成收敛, 在保证优化效率的同时提升模型预测精度。同类模型在测试集上的对比表明, Lasso-SSA-Adaboost模型较KNN模型和随机森林模型, 其预测结果与真实岩性符合率更高, 能预测出可靠的岩性结果, 在研究区应用效果较好。

（ 编辑 陈 娟）

参考文献
[1] 安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018, 33(3): 1029-1034.
AN Peng, CAO Danping. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029-1034. [本文引用:2]
[2] 谷宇峰, 张道勇, 鲍志东. PSO-GBDT识别致密砂岩储集层岩性研究: 以姬塬油田西部长4+5段为例[J]. 矿物岩石地球化学通报, 2021, 40(3): 624-634.
GU Yufeng, ZHANG Daoyong, BAO Zhidong. Lithology prediction of tight sand stone reservoirs using the PSO-GBDT: A case study of the Chang 4+5 members in the western Jiyuan Oilfield[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2021, 40(3): 624-634. [本文引用:1]
[3] 马陇飞, 萧汉敏, 陶敬伟, 等. 基于梯度提升决策树算法的岩性智能分类方法[J]. 油气地质与采收率, 2022, 29(1): 21-29.
MA Longfei, XIAO Hanmin, TAO Jingwei, et al. Intelligent lithology classification method based on GBDT algorithm[J]. Petroleum Geology and Recovery Efficiency, 2022, 29(1): 21-29. [本文引用:2]
[4] 陶宏根, 程日辉, 赵小青, 等. 海拉尔盆地火山碎屑岩的测井响应与应用[J]. 地球物理学报, 2011, 54(2): 534-544.
TAO Honggen, CHENG Rihui, ZHAO Xiaoqing, et al. Well logging response to the volcaniclastic rocks of Hailar Basin and application[J]. Chinese Journal of Geophysics, 2011, 54(2): 534-544. [本文引用:1]
[5] 田玉昆, 周辉, 袁三一. 基于马尔科夫随机场的岩性识别方法[J]. 地球物理学报, 2013, 56(4): 1360-1368.
TIAN Yukun, ZHOU Hui, YUAN Sanyi. Lithologic discrimination method based on Markov rand om-field[J]. Chinese Journal of Geophysics, 2013, 56(4): 1360-1368. [本文引用:1]
[6] 胡红, 曾恒英, 梁海波, 等. 基于主成分分析和学习矢量化的神经网络岩性识别方法[J]. 测井技术, 2015, 39(5): 586-590.
HU Hong, ZENG Hengying, LIANG Haibo, et al. Lithology identification based on Principal Component Analysis and Learning Vector Quantization neural network[J]. Well Logging Technology, 2015, 39(5): 586-590. [本文引用:1]
[7] 牟丹, 王祝文, 黄玉龙, 等. 基于SVM测井数据的火山岩岩性识别: 以辽河盆地东部坳陷为例[J]. 地球物理学报, 2015, 58(5): 1785-1793.
MOU Dan, WANG Zhuwen, HUANG Yulong, et al. Lithological identification of volcanic rocks from SVM well logging data: Case study in the eastern depression of Liaohe Basin[J]. Chinese Journal of Geophysics, 2015, 58(5): 1785-1793. [本文引用:1]
[8] 林香亮, 朱建伟, 刘光寿, 等. 基于PCA-SVM的砂砾岩岩性识别[J]. 长江大学学报(自然科学版), 2020, 17(1): 21-26.
LIN Xiangliang, ZHU Jianwei, LIU Guangshou, et al. Lithology identification of conglomerate based on PCA-SVM[J]. Journal of Yangtze University(Natural Science Edition), 2020, 17(1): 21-26. [本文引用:1]
[9] 苏赋, 马磊, 罗仁泽, 等. 基于改进多分类孪生支持向量机的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2020, 35(1): 174-180.
SU Fu, MA Lei, LUO Renze, et al. Research and application of logging lithology identification based on Improve Multi-Class Twin Support Vector Machine[J]. Progress in Geophysics, 2020, 35(1): 174-180. [本文引用:1]
[10] 李曦, 范翔宇, 王兆峰, 等. 基于PSO-SVM的测井岩性识别方法研究: 以南图尔盖盆地K油田古生界(Pz)储层为例[J]. 地球物理学进展, 2022, 37(2): 617-626.
LI Xi, FAN Xiangyu, WANG Zhaofeng, et al. Logging lithology identification method research based on PSO-SVM： A case of Paleozoic（Pz） reservoir in K Oilfield, South Turgay Basin, Kazakhstan[J]. Progress in Geophysics, 2022, 37(2): 617-626. [本文引用:1]
[11] 张晗, 卢双舫, 李文浩, 等. ΔLogR技术与BP神经网络在复杂岩性致密层有机质评价中的应用[J]. 地球物理学进展, 2017, 32(3): 1308-1313.
ZHANG Han, LU Shuangfang, LI Wenhao, et al. Application of ΔLogR technology and BP neural network in organic evaluation in the complex lithology tight stratum[J]. Progress in Geophysics, 2017, 32(3): 1308-1313. [本文引用:1]
[12] 武中原, 张欣, 张春雷, 等. 基于LSTM循环神经网络的岩性识别方法[J]. 岩性油气藏, 2021, 33(3): 120-128.
WU Zhongyuan, ZHANG Xin, ZHANG Chunlei, et al. Lithology identification based on LSTM recurrent neural network[J]. Lithologic Reservoirs, 2021, 33(3): 120-128. [本文引用:1]
[13] 刘跃杰, 刘书强, 马强, 等. BP神经网络法在三塘湖盆地芦草沟组页岩岩相识别中的应用[J]. 岩性油气藏, 2019, 31(4): 101-111.
LIU Yuejie, LIU Shuqiang, MA Qiang, et al. Application of BP neutral network method to identification of shale lithofacies of Lucaogou Formation in Santanghu Basin[J]. Lithologic Reservoirs, 2019, 31(4): 101-111. [本文引用:1]
[14] 韩启迪, 张小桐, 申维. 基于梯度提升决策树(GBDT)算法的岩性识别技术[J]. 矿物岩石地球化学通报, 2018, 37(6): 1173-1180.
HAN Qidi, ZHANG Xiaotong, SHEN Wei. Lithology identification technology based on Gradient Boosting Decision Tree(GBDT) algorithm[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2018, 37(6): 1173-1180. [本文引用:1]
[15] 刘凯, 邹正银, 王志章, 等. 基于机器学习的火山岩岩性智能识别及预测[J]. 特种油气藏, 2022, 29(1): 38-45.
LIU Kai, ZOU Zhengyin, WANG Zhizhang, et al. Intelligent identification and prediction of lithology of volcanic reservoirs based on machine learning[J]. Special Oil & Gas Reservoirs, 2022, 29(1): 38-45. [本文引用:1]
[16] 彭英, 李克文, 朱应科, 等. 基于FL-XGBoost算法的砂泥岩识别方法: 以胜利油田牛庄地区为例[J]. 油气地质与采收率, 2023, 30(1): 76-85.
PENG Ying, LI Kewen, ZHU Yingke, et al. FL-XGBoost algorithm-based method for identifying sand stone and mudstone: A case study of Niuzhuang area in Shengli Oilfield[J]. Petroleum Geology and Recovery Efficiency, 2023, 30(1): 76-85. [本文引用:1]
[17] 赵彤彤, 张春雷, 张春雨, 等. 基于模糊熵的KNN分类模型在岩性识别中的应用[J]. 计算机工程与应用, 2018, 54(24): 260-265.
ZHAO Tongtong, ZHANG Chunlei, ZHANG Chunyu, et al. Application of KNN classification model based on fuzzy entropy in lithology recognition[J]. Computer Engineering and Applications, 2018, 54(24): 260-265. [本文引用:1]
[18] 张梓童, 张春雷, 张艳, 等. 数据空间结构性及在KNN算法中的应用[J]. 数学的实践与认识, 2019, 49(1): 195-202.
ZHANG Zitong, ZHANG Chunlei, ZHANG Yan, et al. Spatial structure of data and its application in KNN algorithm[J]. Mathematics in Practice and Theory, 2019, 49(1): 195-202. [本文引用:1]
[19] 陈玉林, 李戈理, 杨智新, 等. 基于KNN算法识别合水地区长7储层岩性岩相[J]. 测井技术, 2020, 44(2): 182-185.
CHEN Yulin, LI Geli, YANG Zhixin, et al. Identification of lithology and lithofacies of Chang 7 reservoir in Heshui area by KNN algorithm[J]. Well Logging Technology, 2020, 44(2): 182-185. [本文引用:1]
[20] ZHOU K B, ZHANG J Y, REN Y S, et al. A Gradient Boosting Decision Tree Algorithm combining synthetic minority over-sampling technique for lithology identification[J]. Geophysics, 2020, 85(4): 1-52. [本文引用:1]
[21] DEV V A, EDEN M R. Formation lithology classification using Scalable Gradient Boosted Decision Trees[J]. Computers & Chemical Engineering, 2019, 128: 392-404. [本文引用:1]
[22] 朱林奇, 张冲. 谱聚类-Adaboost集成数据挖掘算法在岩性识别中的应用[J]. 中国科技论文, 2016, 11(5): 545-550.
ZHU Linqi, ZHANG Chong. Application of spectral clustering-Adaboost integrated data mining algorithm in lithology identification[J]. China Sciencepaper, 2016, 11(5): 545-550. [本文引用:1]
[23] XUE J K, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [本文引用:1]
[24] 梁云, 门昌骞, 王文剑. 基于模型决策树的AdaBoost算法[J]. 山东大学学报(理学版), 2023, 58(1): 67-75.
LIANG Yun, MEN Changqian, WANG Wenjian. AdaBoost algorithm based on model decision tree[J]. Journal of Shand ong University(Natural Science), 2023, 58(1): 67-75. [本文引用:1]
[25] 王增帅. 基于集成学习的不平衡数据分类问题研究[D]. 北京: 北京交通大学, 2022.
WANG Zengshuai. Research of the unbalanced data classification problem based on integrated learning[D]. Beijing: Beijing Jiaotong University, 2022. [本文引用:1]