引用本文
季帅良, 曾滨鑫. 基于Transformer-LSTM融合模型的密度测井曲线重构方法[J]. 录井工程, 2025,36(2): 15-23.
JI Shuailiang, ZENG Binxin. Density logging curve reconstruction method based on Transformer-LSTM fusion model[J]. Mud Logging Engineering, 2025,36(2): 15-23.
Doi:10.3969/j.issn.1672-9803.2025.02.003  
Permissions
Copyright©2025, 《录井工程》杂志社
《录井工程》杂志社 所有
基于Transformer-LSTM融合模型的密度测井曲线重构方法
季帅良①,②, 曾滨鑫①,②
①西安石油大学地球科学与工程学院
②西安石油大学陕西省油气成藏地质学重点实验室

作者简介：季帅良 2001年生,西安石油大学地质工程专业在读硕士研究生,研究方向为油气成藏地质。通信地址：710065 陕西省西安市西安石油大学雁塔校区地球科学与工程学院。E-mail：17719689556@163.com

收稿日期: 2025-04-29
摘要

在地质勘探领域,密度测井曲线在确定储层孔隙度、识别气层、判断岩性、划分油水界面、识别流体类型以及提升反演精度等方面具有重要意义。然而,在实际操作中,测井曲线可能因仪器故障、数据传输错误或外部干扰而导致数据丢失或失真。为了解决这一问题,研究提出了一种基于Transformer-LSTM融合模型的密度测井曲线重构方法。该方法利用Transformer的自注意力机制,有效捕捉测井数据中的长距离依赖关系,同时结合长短期记忆神经网络（LSTM）的递归特性从而显著提高重构精度。通过对鄂尔多斯盆地Y区的测井数据进行预处理、模型构建和训练,并与双向门控循环单元（BiGRU）、深度神经网络（DNN）、多元回归分析（Logistic）、时域卷积网络（TCN）及Transformer模型进行了性能对比。结果表明,Transformer-LSTM融合模型在密度测井曲线重构中表现优异,尤其在重构精度和泛化能力方面。实验结果验证了该模型能够重构高精度的密度曲线数据,为地质勘探提供可靠支持。

关键词: 密度测井; 曲线重构; 长距离依赖关系; Transformer架构; LSTM神经网络; 自注意力机制
中图分类号:TE132.1 文献标志码:A
Density logging curve reconstruction method based on Transformer-LSTM fusion model
JI Shuailiang①,②, ZENG Binxin①,②
①School of Earth Sciences and Engineering, Xi′an Shiyou University, Xi′an, Shaanxi 710065, China
②Shaanxi Key Laboratory of Petroleum Accumulation Geology, Xi′an Shiyou University, Xi′an, Shaanxi 710065, China
Abstract

In the field of geologic exploration, density logging curve is of great significance in determining reservoir porosity, identifying gas reservoirs, judging lithology, dividing oil-water interfaces, identifying fluid types, and improving inversion accuracy. However, in practical operation, logs may be lost or distorted due to instrument failures, data transmission errors or external interference. To solve this problem, this paper proposes a density logging curve reconstruction method based on Transformer-LSTM fusion model. This method utilizes Transformer′s self-attention mechanism to effectively capture the long-distance dependency relation in log data, and combines with the recursive characteristics of Long Short-Term Memory （LSTM） to significantly improve the reconstruction accuracy. By preprocessing, model construction and training of log data from Y zone of Ordos Basin, the performance is compared with bidirectional gated recurrent unit （BiGRU）, deep neural networks （DNN）, multiple regression analysis （Logistic）, temporal convolutional network （TCN） and Transformer model. The results show that Transformer-LSTM fusion model performs well in density logging curve reconstruction, especially in terms of reconstruction accuracy and generalization ability. The experimental results verify that the model is capable of reconstructing high-precision density curve data, providing reliable support for geologic exploration.

Keyword: density logging; curve reconstruction; long-distance dependency relation; Transformer architecture; LSTM neural network; self-attention mechanism
0 引言

在地球物理勘探领域, 测井技术能够提供关于地下岩石物理性质的详细信息, 这对于油气勘探、矿产资源评估以及环境监测等方面具有重要的学术和实践意义[1]。密度测井曲线是评估地下岩石孔隙度、渗透性以及流体分布等关键参数的重要依据, 其数据能够直接反映岩石的密度变化, 进而为油气藏的识别和储量估算提供关键信息。然而, 在实际采集过程中, 密度测井曲线常常因技术故障、数据传输错误或外部环境干扰而遭遇数据丢失或失真的问题。这些问题严重影响了数据的完整性, 进而对地质分析和决策构成了极大的障碍[2, 3]。因此, 开发一种有效的密度测井曲线重构方法, 对于提高数据质量和优化勘探效率具有重要的现实意义。

近年来, 随着机器学习技术的迅速发展, 基于数据驱动的测井曲线重构方法逐渐成为研究的热点[4, 5]。目前, 深度学习技术在地球物理学领域得到了广泛应用[6, 7], 涵盖了多个方面, 包括地震反演[8]、测井资料分析[9]、微地震信号拾取[10, 11]以及油藏特征描述[12]等。尽管传统的机器学习算法, 如支持向量机回归（SVR）[13]、随机森林（RF）[14, 15]和极端梯度提升（XGBoost）[16]等, 在一定程度上提高了重构的准确性, 但在处理超长序列数据和识别长距离依赖关系方面仍存在局限。

深度学习中自注意力机制的引入, 为测井曲线的处理提供了新的研究方向。自注意力机制在捕捉长距离依赖关系方面的优势, 有助于提升预测的准确性[17]。已有学者通过研究基于自注意力机制的模型[18, 19, 20], 有效地捕捉了数据中的长距离依赖关系, 从而提高了模型重构的精度。此外, 研究者还提出了利用长短期记忆神经网络（LSTM）及其改进模型来解决测井曲线重构问题[21, 22, 23]。Shi等[24]通过结合卷积神经网络（CNN）、长短期记忆神经网络（LSTM）和注意力机制（Attention）, 降低了测井曲线重构的误差; 翟晓岩等[25]通过融合注意力机制的二维卷积神经网络, 增强了对测井曲线特征的捕捉能力, 从而提高了重构精度; 刘建建等[26]提出了一种基于超参数优化的长短期记忆神经网络（LSTM）技术, 结合自适应超参数调整（ASHA）算法, 优化了LSTM的超参数。然而, 由于该技术对训练数据的质量和数量要求较高, 可能会影响最终生成的测井曲线的准确性。

本文提出了一种基于Transformer-LSTM融合模型的密度测井曲线重构方法。该方法结合Transformer的自注意力机制和LSTM的递归特性, 旨在充分发挥两者在序列建模中的互补优势, 提高重构精度。模型选择与密度相关的测井曲线作为输入特征, 以确保密度曲线重构的准确性和真实性。通过将Transformer-LSTM融合模型的重构结果与双向门控循环单元（BiGRU）、深度神经网络（DNN）、多元回归分析（Logistic）、时域卷积网络（TCN）及Transformer模型的重构结果进行比较, 并在鄂尔多斯盆地Y区应用, 验证了该模型在重构精度和泛化能力方面的优势。实验结果表明, Transformer-LSTM融合模型在处理测井数据中存在的长距离依赖关系以及提高重构质量方面表现出色, 具有较好的重构结果。

1 Transformer-LSTM融合模型构建

本研究采用Transformer-LSTM融合模型架构, 该模型通过结合Transformer结构中的自注意力机制与LSTM网络的递归特性, 充分发挥了两者在序列建模中的互补优势。

1.1 Transformer模块

本实验采用的Transformer模块基于自注意力机制构建, 由以下核心部分组成。

1.1.1 自注意力机制

自注意力机制是Transformer模型的核心, 允许模型在处理每个元素（如单词或字符）时, 考虑整个序列中的所有元素。自注意力机制有效克服了传统循环神经网络在处理长序列数据时容易出现的梯度消失问题, 同时支持并行计算, 极大地提升了运算效率[27, 28]。其计算公式如下：

Attention（Q，K，V）=softmaxQKTdKV（1）

式中：Q为查询向量; K为键向量; V为值向量; dK为构成Q和K的矩阵的列数维度; T为转置操作。

1.1.2 多头注意力层

多头注意力机制是自注意力机制的一种扩展形式。由Bahdanau等[29]首次应用于神经机器翻译领域, 该机制通过多次复制自注意力机制（即“ 头” ）, 使每个“ 头” 能学习数据的不同部分及其在不同子空间中的表示。这些“ 头” 的输出经过拼接后, 通过一个线性层进行处理, 从而使模型能够在多维度子空间中捕获信息[30]。此机制的引入增强了模型的容量, 使其能够更为丰富地表示数据。其计算公式如下：

MultiHead（Q，K，V）=Contact（h1，h2，…，hi，…，hj）WO（2）

hi=Attention（QWiQ，KWiK，VWiV）（3）

式中： j为“ 头” 的数量; hi为第i个“ 头” 的输出, i=1, 2, …, j; WO为输出变换矩阵; WiQ、 WiK、 WiV分别为第i个注意力“ 头” Q、K、V的权重矩阵。

1.1.3 编码器

编码器（Encoder）由多个层次构成, 每一层均包含自注意力机制和前馈神经网络, 从而有效捕捉输入数据的全局依赖关系, 同时提取更深层次的特征[31]。在Transformer的编码器中, 数据首先经过自注意力模块, 生成一个加权后的特征向量Z。在获得Z之后, 其将被传递至编码器的下一个模块, 即前馈神经网络。该前馈神经网络由两层全连接层组成, 其中第1层采用ReLU激活函数, 第2层则使用线性激活函数。其数学表达式如下：

FFN（Z）=max（0，ZW1+b1）W2+b2（4）

式中： W1、 W2分别为第1、2层全连接的权重矩阵; b1为第1层全连接层的偏置项, 其维度与 W1的列数相同; b2为第2层全连接层的偏置项, 其维度与 W2的行数相同; max（0，ZW1+b1）W2为ReLU激活函数的应用。

1.1.4 位置编码

由于Transformer模型的自注意力机制本身并不包含关于单词顺序的信息, 因此需要额外的位置编码来补充这一顺序信息。在Transformer模型的原始版本中, 采用了基于正弦和余弦函数的相对位置编码。该编码方法利用不同频率的正弦和余弦波形来表示序列中各个位置的信息, 从而使模型能够识别单词之间的相对位置及其绝对位置。位置编码的计算方法如下：

PE（p，2m）=sin（p/100002mdm）（5）

PE（p，2m+1）=cos（p/100002mdm）（6）

式中：p为当前序列的位置; m为维度; dm为输入特征的维度。

1.2 LSTM模块

在序列数据分析中, 准确捕捉时间序列的长期和短期依赖关系对于提高预测精度至关重要。在传统的Transformer模型中, 解码层在自然语言翻译等任务中表现优异, 然而在时间序列预测, 特别是在测井曲线重构任务中, 解码层被线性层所替代, 这在处理短数据集时可能导致显著的预测偏差。为提高预测的准确性, 本研究引入了一种基于长短期记忆神经网络的解码层重构方案, 以增强模型在测井曲线重构任务中的性能。

Hochreiter等[32]在1997年首次提出长短期记忆神经网络（LSTM）, 包含输入门、遗忘门、输出门以及单元状态。这些机制使得LSTM能够有效地捕捉序列数据中的长期依赖关系, 避免传统递归神经网络（RNN）中存在的梯度消失问题[33, 34]。在实验模型中, LSTM模块被用作解码层, 接收Transformer编码器的输出结果, 并在此基础上进一步提炼和加工信息。通过这种方式, LSTM增强了模型对时间序列数据动态特征的解析能力, 从而提高了预测的准确性。

1.3 Transformer-LSTM融合模型

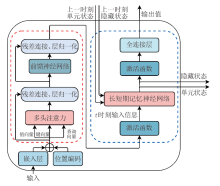
本研究采用了Transformer-LSTM融合模型, 旨在处理序列数据并提升预测精度。该模型结合了Transformer的自注意力机制与LSTM的递归结构, 以全面捕捉时间序列中的长短期依赖关系, Transformer-LSTM融合模型架构如图1所示。

图1 Transformer-LSTM融合模型架构

对于输入数据 x∈RB·T·dinput, 首先通过嵌入层映射至隐藏维度：

h0=x·Wemb+bemb（7）

式中： R为实数集; B为批大小; T为序列长度; dinput为输入特征维度; h0为嵌入后的表示; Wemb与 bemb分别为嵌入层的权重矩阵和偏置向量。

在Transformer模块中, 通过位置编码将位置信息添加到隐藏表示 h0中, 以便捕捉序列之间的关系, 对应公式如下：

h1=h0+PE（h0）（8）

式中： h1为对嵌入层得到的隐藏表示; PE（· ）为基于正弦和余弦函数的位置编码。

接下来, 通过多头注意力机制来捕捉全局依赖关系。在Transformer模块中, 每个子层的输出不仅包含当前层的计算结果, 还包含输入到该层的原始输入, 即残差连接, 这有助于缓解梯度消失问题。此外, 每个子层输出后都进行层归一化处理, 以进一步稳定训练过程。利用前馈神经网络进一步提取特征, 从而获得Transformer编码器的最终输出 h2。

再将Transformer编码器的输出作为LSTM的输入, 以提取时间序列中的短期依赖。其对应公式如下：

h2=TransformerEncoder（h1）（9）

h3, （ht，ct）=LSTM（h2，（ht-1，ct-1））（10）

式中： h2为Transformer编码器的输出序列; h3为LSTM解码器的输出序列; ht、 ct分别为LSTM在当前时间步的隐藏状态和单元状态; ht-1、 ct-1分别为LSTM在上一时间步的隐藏状态和单元状态。

LSTM通过引入激活函数来控制信息的流动：遗忘门和输入门使用sigmoid激活函数, 决定信息保留或丢弃; 单元状态更新使用tanh激活函数, 用于更新单元状态; 输出门使用sigmoid激活函数, 控制信息输出到隐藏状态。

最后输出通过线性层进行生成：

y=hT·Wout+bout（11）

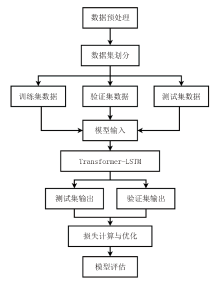
式中：y为整个模型流程的最终输出结果; hT为LSTM最后一个时间步的隐藏状态; Wout为输出层的权重矩阵; bout为输出层的偏置项。

2 模型应用与优化

Transformer-LSTM融合模型通过一系列数据流步骤处理序列预测任务, 数据流程如图2所示。先对原始数据进行预处理, 对数据进行异常值清理后, 再通过线性回归模型选取合适的模型输入特征, 然后对数据进行标准化以及数据集划分。在模型训练阶段, 将数据输入到Transformer编码器, 利用其自注意力机制捕捉数据中的长距离依赖关系, 然后数据流经LSTM层, 进一步提炼时间序列中的短期依赖特征, 最终由线性层输出预测结果, 并通过损失函数量化预测值与真实值之间的偏差。

图2 Transformer-LSTM融合模型数据流程

2.1 数据预处理

实验选取鄂尔多斯盆地Y区长8段的测井资料, 该区域地质条件稳定, 数据完整。选取3口井中与密度相关的测井曲线数据用于模型训练, 涵盖声波时差、自然电位、补偿中子、地层真电阻率和自然伽马等关键参数。

首先对数据进行异常值清理, 然后通过线性回归模型选取与测井密度相关性更好的测井参数作为输入特征, 最后进行数据标准化以提高模型的泛化能力和鲁棒性。

2.1.1 异常值清理

对所获取的测井资料进行数据清理, 剔除其中异常值和重复值。

2.1.2 输入特征选取

采用线性回归模型对密度测井曲线数据与其他测井曲线数据之间的相关性进行分析。决定系数R² 是衡量这种线性关系强度的重要指标, 基于原始数据计算, 其取值范围为0到1。R² 值越接近1, 表明相关性越强。R² 的计算公式如下：

R2=1-Sr/St（12）

式中： Sr为残差平方和, 即密度测井曲线数据实际值与基于线性关系计算值之差的平方和; St为总平方和, 即密度测井曲线数据实际值与该数据实际值平均值之差的平方和。

如图3所示, 密度曲线与声波时差及补偿中子之间存在显著的相关性, 与地层真电阻率相关性较弱, 与自然伽马及自然电位相关性很差。基于这一发现, 本实验选择声波时差、补偿中子与地层真电阻率3种测井曲线数据作为模型输入特征。

图3 其他测井曲线与密度曲线数据交会图

2.1.3 数据标准化

测井曲线因作业差异存在系统误差, 需通过标准化处理提高对比性。采用z-score（正规化）方法对特征和标签进行处理, 从而使数据符合标准正态分布。此过程有助于消除不同量纲特征的差异, 优化模型的训练效率, 并增强模型对数据的泛化能力。

yi=（xi-x̅）/s（13）

式中： yi为样本数据标准化值; xi为样本数据原始值; x̅为样本数据的均值; s为样本数据的标准差。

2.1.4 数据集划分

数据预处理后训练集包含15 488个测井曲线数据记录, 采样深度间隔为0.125 m。从训练集中提取其总量的十分之一作为测试集（训练集的数据量不变）。在确保训练集数据完整性的同时, 通过测试集对模型训练的泛化能力进行验证。从Y区M 31井中截取1 552条数据作为验证集, 为保证实验准确性, 这些数据已从井段数据中剔除。

2.2 模型优化

在模型训练过程中, 优化器与优化算法的选择对于提升模型的学习效率和性能至关重要。优化器的选择不仅直接影响模型的收敛速度, 还决定了训练过程的稳定性; 而参数优化算法则通过对超参数的精细调整, 进一步提升模型的性能。通过精心选择优化器与优化算法优化超参数, 确保模型在训练过程中的高效性和稳定性, 为地质勘探提供可靠的预测支持。

2.2.1 优化器选择

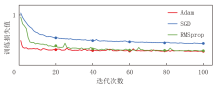
为了提高模型的学习效率和性能, 需要利用优化器以指导模型的优化过程。本实验选取Adam、SGD、RMSprop共3种优化器进行比较, 其训练损失函数对比如图4所示。从图4可以看出, Adam优化器表现出显著的优越性。从训练初期开始, Adam优化器的损失值迅速下降, 并且在整个训练过程中保持较低且稳定的损失水平, 这表明Adam优化器在学习率调整方面具有高效性和稳定性。相比之下, SGD优化器虽然在初期同样能够快速降低损失, 但在训练中期的收敛速度较慢, 且其损失值在整个训练过程中始终高于Adam优化器, 这表明SGD优化器在某些训练阶段需要更为细致的学习率调整以优化模型性能。RMSprop优化器在初期的损失下降速度与Adam优化器相近, 但在训练后期表现出较大的波动性, 这可能导致模型训练过程中的不稳定性。Adam优化器结合自适应学习率调整和动量项的特性, 相较于传统的SGD优化器, Adam优化器能够自动调整学习率, 从而显著减少了手动调整学习率的需求, 使训练过程更加高效。与RMSprop优化器相比, Adam优化器引入了动量项, 因而有助于加速模型的收敛过程。因此最终选择Adam优化器来指导模型参数的优化过程。

图4 不同优化器训练损失函数曲线对比

2.2.2 优化算法

为了对模型参数进行优化, 引入贝叶斯参数优化算法[35]。该算法的理论基础为贝叶斯定理以及高斯过程, 其核心思路在于构建目标函数的代理模型, 以此作为优化过程中的关键工具。在每轮迭代过程中, 依据已有的观测数据对代理模型进行更新, 随后借助更新后的代理模型来确定下一轮的参数选择方向。通过这种方式, 能够在参数空间内以一种更具智能性与高效性的方式筛选出下一个参数点, 加速对目标函数最优解的探寻进程, 进而提升模型参数优化的整体效率与效果。优化后的模型参数如表1所示。

表1 优化后的模型参数

通过贝叶斯优化算法筛选出的最优参数配置, 能够使Transformer-LSTM融合模型在密度测井曲线重构任务中达到最佳性能。最终确定最优参数配置如下：批处理大小为64, 学习率为0.000 286, LSTM层数为1, Dropout率为0.35, Transformer隐藏维度为128, Transformer注意力头数为2, Transformer前馈神经网络扩展倍数为2。

3 实验结果及分析
3.1 不同模型损失对比

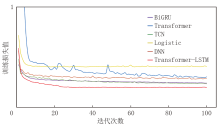
为验证Transformer-LSTM融合模型拟合精度, 本文选用BiGRU、DNN、Logistic、TCN及单独的Transformer模型进行对比。图5展示了不同模型在训练阶段的损失变化情况。从不同模型的训练损失对比分析中可以看出, Transformer-LSTM融合模型以其快速的损失下降和在整个训练周期内持续的低损失值而优于其他对比模型。这表明Transformer-LSTM融合模型在序列数据处理过程中具有高效的学习能力和良好的拟合精度。与BiGRU、Transformer、TCN、Logistic和DNN模型相比, Transformer-LSTM融合模型在损失下降速度和最终损失值方面均展现出优势, 尤其是在训练后期的稳定性和泛化能力上, 这在处理具有时间序列特征的数据时尤为重要。

图5 不同模型训练损失函数曲线对比

3.2 模型重构结果

为评估Transformer-LSTM融合模型在重构密度测井曲线方面的表现, 将其与BiGRU、DNN、Logistic、TCN以及Transformer模型在鄂尔多斯盆地Y区M 31井的重构结果进行对比。通过在相同验证集上进行测试, 对这些模型的性能进行对比分析。对比结果如图6所示, 图中红色曲线表示不同模型预测的密度测井数据结果, 黑色曲线表示密度测井数据的真实值。

图6 M 31井密度测井曲线重构对比图

Transformer-LSTM融合模型的预测曲线与真实曲线在趋势和波动上保持一致, 尤其是在2 150~2 300 m井段, 预测曲线能够准确捕捉到真实曲线的波动及其峰谷特征。相比之下, BiGRU模型的预测结果与真实曲线虽然整体趋势相似, 但在某些井段（如2 300 m附近）存在一定的偏差, 尤其是在曲线的某些峰值和谷值处, 其预测精度低于Transformer-LSTM融合模型; DNN模型的预测结果尽管在大部分区域与真实曲线保持一致, 但在某些井段（如2 250~2 300 m）内, 预测曲线的波动性较大, 且与真实曲线的拟合度低于Transformer-LSTM融合模型; TCN模型在2 200 m波动区域的表现与Transformer-LSTM融合模型相近, 但在2 150~2 200 m井段, 预测曲线与真实曲线相比存在一定的偏差; Logistic模型的表现相对较弱, 尤其是在2 150~2 300 m井段, 预测曲线与真实曲线的偏差较大, 显示出其在处理此类数据时的局限性; Transformer模型在2 200 m波动区域的表现尚可, 但在2 200~2 250 m井段, 预测曲线的波动性较大, 导致与真实曲线的拟合度降低。总体而言, Transformer-LSTM融合模型在预测准确性和稳定性方面优于其他模型。

3.3 重构误差分析

为了深入评估模型的泛化能力, 在实验环境和所采用的实验数据保持一致的前提下, 利用均方误差（MSE）、平均绝对误差（MAE）、均方根误差（RMSE）以及R² , 分别对Transformer-LSTM、BiGRU、DNN、Logistic、TCN和Transformer模型在鄂尔多斯盆地Y区M 31井的密度测井曲线预测结果进行综合评估。

3.3.1 评价指标

MSE衡量的是预测值与实际值之间差的平方的平均值。MSE越小, 表示模型预测越准确。计算公式为：

MSE=1N∑i=1Nŷi-yi2（14）

MAE衡量的是预测值与实际值之间差的绝对值的平均值。MAE越小, 表示模型预测越准确。计算公式为：

MAE=1N∑i=1Nŷi-yi（15）

RMSE是MSE的平方根, 与MAE类似, 但对大的误差给予更大的权重。RMSE越小, 表示模型预测越准确。计算公式为：

RMSE=1N∑i=1Nŷi-yi2（16）

上列各式中：N为样本总数; ŷi为重构曲线数据。

R² 衡量的是模型解释的因变量的方差比例, 基于模型预测结果和实际值标准化后的值计算。R² 越接近1, 表示模型预测越准确。计算公式同公式（12）。

3.3.2 模型重构误差分析

各模型在测试集上的评价指标数据如表2所示。该结果显示, Transformer-LSTM融合模型在MSE、MAE、RMSE和R² 方面均具有优势。这表明该模型在最小化预测误差和解释数据变异性方面具有优势。

表2 不同模型评价指标数据

实验结果表明, Transformer-LSTM融合模型在密度测井曲线重构中, 表现优于传统机器学习方法及部分深度学习方法, 验证了Transformer-LSTM融合模型在处理测井数据方面的有效性, 并在预测精度、稳定性和解释能力等方面展现出显著优势。

4 结论

将Transformer-LSTM融合模型应用于密度测井曲线重构是一项相对较新的研究尝试。对鄂尔多斯盆地Y区测井数据的实验结果表明, 该方法在重构精度和泛化能力方面具有显著优势。通过实验分析, 得出以下结论：

（1）Transformer-LSTM融合模型在密度测井曲线重构中表现出卓越的性能, 超越了传统机器学习模型（如Logistic、DNN等）和深度学习模型（如BiGRU、TCN等）。

（2）Transformer-LSTM融合模型在捕捉测井数据中的长距离依赖关系方面表现优异, 这主要归功于其自注意力机制的引入。多头自注意力机制使模型能够从多维度子空间中进行学习, 从而增强了对信息的捕获能力。此外, 残差连接和层归一化技术有助于稳定训练过程、缓解梯度消失和防止过拟合, 从而提升了模型的泛化能力。同时, LSTM的递归特性增强了对时间序列短期动态依赖的捕捉, 与Transformer的长距离依赖捕捉能力形成互补, 共同提升了重构精度。

（3）在独立测试集上, Transformer-LSTM融合模型展现了卓越的泛化性能, 其重构的密度曲线与实际测井数据高度吻合。模型预测结果具有较高的可靠性, 能够为地质勘探提供精确的数据支撑, 验证了该模型在测井密度曲线重构中的有效性与实用性。

（编辑 陈娟）

参考文献
[1] 李宁, 徐彬森, 武宏亮, 等. 人工智能在测井地层评价中的应用现状及前景[J]. 石油学报, 2021, 42(4): 508-522.
LI Ning, XU Binsen, WU Hongliang, et al. Application status and prospects of artificial intelligence in well logging and formation evaluation[J]. Acta Petrolei Sinica, 2021, 42(4): 508-522. [本文引用:1]
[2] 王欢欢, 赵彬, 刘建新, 等. 基于多头注意力机制的TCN-BiGRU密度测井曲线重构方法[J]. 地球物理学进展, 2025, 40(2): 592-604.
WANG Huanhuan, ZHAO Bin, LIU Jianxin, et al. Density logging curve reconstruction method based on TCN-BiGRU with multi-head attention mechanism[J]. Progress in Geophysics, 2025, 40(2): 592-604. [本文引用:1]
[3] 范翔宇, 孟凡, 邓娟, 等. 基于自动机器学习的测井曲线重构技术[J]. 天然气工业, 2024, 44(9): 38-54.
FAN Xiangyu, MENG Fan, DENG Juan, et al. Well logs reconstruction based on automatic machine learning technology[J]. Natural Gas Industry, 2024, 44(9): 38-54. [本文引用:1]
[4] 金永吉, 张强, 王毛毛. 基于遗传神经网络算法的测井曲线重构技术[J]. 地球物理学进展, 2021, 36(3): 1082-1087.
JIN Yongji, ZHANG Qiang, WANG Maomao. Well logging curve reconstruction based on genetic neural network[J]. Progress in Geophysics, 2021, 36(3): 1082-1087. [本文引用:1]
[5] 熊文君, 肖立志, 袁江如, 等. 基于深度强化学习的测井曲线自动深度校正方法[J]. 石油勘探与开发, 2024, 51(3): 553-564.
XIONG Wenjun, XIAO Lizhi, YUAN Jiangru, et al. Automatic depth matching method of well log based on deep reinforcement learning[J]. Petroleum Exploration and Development, 2024, 51(3): 553-564. [本文引用:1]
[6] 匡立春, 刘合, 任义丽, 等. 人工智能在石油勘探开发领域的应用现状与发展趋势[J]. 石油勘探与开发, 2021, 48(1): 1-11.
KUANG Lichun, LIU He, REN Yili, et al. Application and development trend of artificial intelligence in petroleum exploration and development[J]. Petroleum Exploration and Development, 2021, 48(1): 1-11. [本文引用:1]
[7] 赵改善. 石油物探智能化发展之路: 从自动化到智能化[J]. 石油物探, 2019, 58(6): 791-810.
ZHAO Gaishan. Road to intelligent petroleum geophysical exploration: From automatic to intelligent[J]. Geophysical Prospecting for Petroleum, 2019, 58(6): 791-810. [本文引用:1]
[8] 周杰. 神经网络法地震反演应用及效果[J]. 断块油气田, 2010, 17(5): 560-562, 570.
ZHOU Jie. Application and effect of seismic inversion based on neural network[J]. Fault-Block Oil & Gas Field, 2010, 17(5): 560-562, 570. [本文引用:1]
[9] 姜效典, 李巍然. 应用瓦尔什变换和人工神经网络划分岩层和岩性识别[J]. 石油学报, 1994, 15(4): 17-22.
JIANG Xiaodian, LI Weiran. The applications of Walsh transform and artificial neural network to identify the rock stratum and lithology automatically[J]. Acta Petrolei Sinica, 1994, 15(4): 17-22. [本文引用:1]
[10] 王博爱, 杨瑞召, 李德伟, 等. 基于循环神经网络的微地震有效信号自动识别[J]. 断块油气田, 2021, 28(5): 649-654, 690.
WANG Boai, YANG Ruizhao, LI Dewei, et al. Automatic recognition of effective signals for microseismic based on recurrent neural network[J]. Fault-Block Oil & Gas Field, 2021, 28(5): 649-654, 690. [本文引用:1]
[11] 罗浩, 彭代平, 黄鹏, 等. NARX神经网络微地震P波有效事件自动拾取方法研究[J]. 地球物理学进展, 2024, 39(6): 2345-2356.
LUO Hao, PENG Daiping, HUANG Peng, et al. Research on automatic picking method of effective events of microseismic P-wave in NARX neural network[J]. Progress in Geophysics, 2024, 39(6): 2345-2356. [本文引用:1]
[12] 郑松青, 计秉玉, 顾浩, 等. 基于节点网络模型的缝洞型碳酸盐岩油藏动态描述技术[J]. 石油学报, 2024, 45(9): 1422-1431.
ZHENG Songqing, JI Bingyu, GU Hao, et al. Dynamic description technology for fracture-vug carbonate reservoirs based on node network model[J]. Acta Petrolei Sinica, 2024, 45(9): 1422-1431. [本文引用:1]
[13] LUO S Y, XU T J, WEI S J. Prediction method and application of shale reservoirs core gas content based on machine learning[J]. Journal of Applied Geophysics, 2022, 204: 104741. [本文引用:1]
[14] 刘超, 唐锡彬, 邓冬梅, 等. 基于支持向量机回归的岩体变形模量预测[J]. 地质科技情报, 2018, 37(5): 275-280.
LIU Chao, TANG Xibin, DENG Dongmei, et al. Prediction of rock deformation modulus based on support vector machine regression[J]. Geological Science and Technology Information, 2018, 37(5): 275-280. [本文引用:1]
[15] FENG R H, GRANA D, BALLING N. Imputation of missing well log data by rand om forest and its uncertainty analysis[J]. Computers & Geosciences, 2021, 152(4): 104763. [本文引用:1]
[16] 张家臣, 邓金根, 谭强, 等. 基于XGBoost的测井曲线重构方法[J]. 石油地球物理勘探, 2022, 57(3): 697-705.
ZHANG Jiachen, DENG Jin′gen, TAN Qiang, et al. Reconstruction of well logs based on XGBoost[J]. Oil Geophysical Prospecting, 2022, 57(3): 697-705. [本文引用:1]
[17] 汪敏, 郭鑫平, 唐洪明, 等. 深度Transformer迁移学习的页岩气储层核心参数预测案例[J]. 地球物理学报, 2023, 66(6): 2592-2610.
WANG Min, GUO Xinping, TANG Hongming, et al. Prediction case of core parameters of shale gas reservoirs through deep Transformer transfer learning[J]. Chinese Journal of Geophysics, 2023, 66(6): 2592-2610. [本文引用:1]
[18] RAHMAN A U, ALSENANI Y, ZAFAR A, et al. Enhancing heart disease prediction using a self-ttention-based transformer model[J]. Scientific Reports, 2024, 14(1): 514-514. [本文引用:1]
[19] NASIM M Q, SINGHA ROY P N, MITRA A. Efficient self-attention based joint optimization for lithology and petrophysical parameter estimation in the Athabasca Oil Sand s[J]. Journal of Applied Geophysics, 2024, 230: 105532. [本文引用:1]
[20] XU C W, WANG Y Y, BARATI FARIMANI A. TransPolymer: A Transformer-based language model for polymer property predictions[J]. Computational Materials, 2023, 9: 64. [本文引用:1]
[21] 刘梦, 韩建, 曹志民, 等. 基于模态分解与LSTM注意表征的测井曲线重构研究[J]. 电子学报, 2024, 52(4): 1399-1410.
LIU Meng, HAN Jian, CAO Zhimin, et al. Logging curves reconstruction based on mode decomposition and LSTM-attention model[J]. Acta Electronica Sinica, 2024, 52(4): 1399-1410. [本文引用:1]
[22] LIANG J Y, LU Y X, SU M M. Hga-lstm: LSTM architecture and hyperparameter search by hybrid GA for air pollution prediction[J]. Genetic Programming and Evolvable Machines, 2024, 25(2): 20. [本文引用:1]
[23] 张海涛, 杨小明, 陈阵, 等. 基于增强双向长短时记忆神经网络的测井数据重构[J]. 地球物理学进展, 2022, 37(3): 1214-1222.
ZHANG Haitao, YANG Xiaoming, CHEN Zhen, et al. Log data reconstruction method based on enhanced bidirectional long short-term memory neural network[J]. Progress in Geophysics, 2022, 37(3): 1214-1222. [本文引用:1]
[24] SHI M J, YANG B H, CHEN R, et al. Logging curve prediction method based on CNN-LSTM-attention[J]. Earth Science Informatics, 2022, 15(4): 2119-2131. [本文引用:1]
[25] 翟晓岩, 高刚, 李勇根, 等. 融合注意力机制的二维卷积神经网络测井曲线重构方法[J]. 石油地球物理勘探, 2023, 58(5): 1031-1041.
ZHAI Xiaoyan, GAO Gang, LI Yonggen, et al. Reconstruction method of logging curves by 2D convolutional neural network integrating attention mechanism[J]. Oil Geophysical Prospecting, 2023, 58(5): 1031-1041. [本文引用:1]
[26] 刘建建, 周军, 余卫东, 等. 基于超参数优化LSTM的声波测井曲线生成技术[J]. 石油物探, 2024, 63(5): 1061-1074.
LIU Jianjian, ZHOU Jun, YU Weidong, et al. Acoustic log curve reconstruction based on hyperparameter optimized LSTM[J]. Geophysical Prospecting for Petrolum, 2024, 63(5): 1061-1074. [本文引用:1]
[27] 吴嘉俊, 苏春, 张玉茹. 基于双重自注意力机制和长短时记忆网络的剩余寿命预测[J]. 系统工程与电子技术, 2024, 46(6): 1986-1994.
WU Jiajun, SU Chun, ZHANG Yuru. Remaining useful life prediction based on double self-attention mechanism and long short-term memory network[J]. Systems Engineering and Electronics, 2024, 46(6): 1986-1994. [本文引用:1]
[28] 张帆, 姚德臣, 姚圣卓, 等. 基于Transformer-LSTM网络的轴承寿命预测[J]. 振动与冲击, 2024, 43(6): 320-328.
ZHANG Fan, YAO Dechen, YAO Shengzhuo, et al. Lifetime prediction of bearings based on the Transformer-LSTM network[J]. Journal of Vibration and Shock, 2024, 43(6): 320-328. [本文引用:1]
[29] BAHDANAU D, CHO K, BENGIO Y. Neural machine translation by jointly learning to align and translate[J]. Computer Science, 2014, 1: 1-15. [本文引用:1]
[30] 陈嘉俊, 刘波, 林伟伟, 等 . 基于Transformer的时间序列预测方法综述[J/OL]. 计算机科学, 1-17[2025-01-02]. http://kns.cnki.net/kcms/detail/50.1075.TP.20241030.0909.002.html.
CHEN Jiajun, LIU Bo, LIN Weiwei, et al. Summary of time series prediction methods based on Transformer[J/OL]. Computer Science, 1-17[2025-01-02]. http://kns.cnki.net/kcms/detail/50.1075.TP.20241030.0909.002.html. [本文引用:1]
[31] 王云宏. 基于Transformer神经网络的瞬变电磁法数值模拟[J]. 煤田地质与勘探, 2024, 52(11): 151-159.
WANG Yunhong. Transient electromagnetic numerical simulation based on the Transformer neural network[J]. Coal Geology & Exploration, 2024, 52(11): 151-159. [本文引用:1]
[32] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. [本文引用:1]
[33] LI J, GAO G Z. Digital construction of geophysical well logging curves using the LSTM deep-learning network[J]. Frontiers in Earth Science, 2023, 10: 1041807. [本文引用:1]
[34] 周恒, 武中原, 张欣, 等. 基于LSTM循环神经网络的横波预测方法[J]. 断块油气田, 2021, 28(6): 829-834.
ZHOU Heng, WU Zhongyuan, ZHANG Xin, et al. Shear wave prediction method based on LSTM recurrent neural network[J]. Fault-Block Oil & Gas Field, 2021, 28(6): 829-834. [本文引用:1]
[35] 曾滨鑫, 肖晖, 郝子眉, 等. 基于VAE-BiGRU-Attention模型的储层孔隙度预测: 以中-低渗砂岩储层为例[J]. 地球物理学进展, 2025, 40(2): 658-669.
ZENG Binxin, XIAO Hui, HAO Zimei, et al. Reservoir porosity prediction using the VAE-BiGRU-Attention model: An example study of middle-low permeability sand stone reservoir[J]. Progress in Geophysics, 2025, 40(2): 658-669. [本文引用:1]