引用本文
田志山, 李景元, 王俊, 赵民, 吕鹏福, 郧国立. 基于pH和温度影响补偿的离子选择电极精确测量方法[J]. 录井工程, 2025,36(3): 72-78.
TIAN Zhishan, LI Jingyuan, WANG Jun, ZHAO Min, LYU Pengfu, YUN Guoli. Precise measurement methods for ion selective electrodes based on pH and temperature influence compensation[J]. Mud Logging Engineering, 2025,36(3): 72-78.
Doi:10.3969/j.issn.1672-9803.2025.03.011  
Permissions
Copyright©2025, 《录井工程》杂志社
《录井工程》杂志社 所有
基于pH和温度影响补偿的离子选择电极精确测量方法
田志山①, 李景元②, 王俊②, 赵民②, 吕鹏福②, 郧国立②
①中国石油大庆钻探工程有限公司
②中国石油大庆钻探地质录井公司
通讯作者：赵民 高级工程师,1986年生,2012年毕业于燕山大学油气井工程专业,主要从事录井工艺研发相关工作。通信地址：163413 黑龙江省大庆市让胡路区银海街地质录井公司9号楼。E-mail：zhaomin007@cnpc.com.cn

作者简介：田志山 高级工程师,1973年生,1994年毕业于长春地质学院能源系石油地质勘查专业,主要从事地质工程管理相关工作。通信地址：163453 黑龙江省大庆市让胡路区爱国路12号大庆钻探工程有限公司。E-mail：tianzhishan@cnpc.com.cn

收稿日期: 2025-07-17
摘要

钻井作业中钻头是否在目的层中穿行,可根据钻井液离子浓度变化判断。然而,常规人工化学滴定测量存在操作周期长、误差大、受人为因素影响大的问题;而部分实验室采用的离子选择电极法测量精度受pH值与温度的影响较大,无法满足现场需求。为此,提出了一种针对钻井液pH值与温度干扰的离子选择电极测量误差补偿方法。在总结离子选择电极的测量原理基础上,通过分析pH值与温度参数对离子选择电极的影响特性,建立氯离子浓度测量的实验方案;随后根据pH值与温度的实验数据与模型分析,在能斯特方程中引入pH和温度线性补偿项来消除待测溶液pH和温度变化对电极测量电位的干扰,建立离子选择电极的pH和温度补偿模型;最后通过实际采集的不同温度与pH值下的离子浓度参数进行模型验证,经过补偿之后的氯离子浓度测量误差均在10%以内,满足现场实际需求。

关键词: 离子选择电极; pH值影响; 温度影响; 氯离子浓度; 补偿模型
中图分类号:TE132.1 文献标志码:A
Precise measurement methods for ion selective electrodes based on pH and temperature influence compensation
TIAN Zhishan①, LI Jingyuan②, WANG Jun②, ZHAO Min②, LYU Pengfu②, YUN Guoli②
①Daqing Drilling Engineering Company Limited, CNPC, Daqing, Heilongjiang 163411, China
②Geo-Logging Company of CNPC Daqing Drilling Engineering Company Limited, Daqing, Heilongjiang 163411, China
Abstract

During drilling operations, the penetration of the drill bit into the target formation and the occurrence of formation penetration can be determined by monitoring changes in the ion concentration of the drilling fluid. However, conventional manual chemical titration measurements suffer from lengthy operation cycles, significant errors, and substantial influence from human factors. The ion selective electrodes （ISE） method employed by some laboratories suffers from significant measurement inaccuracies influenced by pH and temperature, rendering it unsuitable for field applications. This paper therefore proposes an error compensation method for ISE measurements affected by drilling fluid pH and temperature interference. Building upon an overview of ISE measurement principles, the paper analyzes the influence characteristics of pH and temperature parameters on ISE and establishes an experimental scheme for chloride ion concentration measurement. Subsequently, based on experimental data and model analysis of pH and temperature, linear compensation terms for pH and temperature are introduced into the Nernst equation to eliminate interference from pH and temperature variations in the solution to be measured. This establishes pH and temperature compensation models for ion selective electrodes. Finally, the models are validated using ion concentration parameters are actually collected at different temperatures and pH values. After compensation, the measurement errors for chloride ion concentration are consistently within 10%, meeting field requirements.

Keyword: ion selective electrodes; pH influence; temperature influence; chloride ion concentration; compensation model
0 引言

钻井过程中钻井液发挥着多种功能, 包括降温、润滑、减少钻机摩擦、调节岩层和井壁压力、获得井下信息等[1]。在复杂多变的地质勘探条件下, 稳定性较强, 且有较好润滑性和抑制性的水基钻井液可以最大限度地保护储层, 从而确保单井的产量。钻井过程中, 钻井液离子浓度的变化往往预示着井下情况的变化：钻遇溶洞地层时, 因其中的大量饱和盐水与钻井液进行置换, 进而破环钻井液性状, 降低井底压力, 从而引发溢流甚至井喷事故[2]。钻井作业中, 也可根据钻井液离子浓度变化判断钻头是否处于目的层。如果钻井液性质配比保持不变, 结合滤液中阴阳离子种类、浓度变化及其他录井数据, 可初步确定目标层界面, 为钻探提供技术支持[3, 4]。

目前, 对氯离子、钾离子、硫离子等的浓度测量主要采用标准溶液滴定滤液法, 但该方法需提取滤液和调节pH值, 耗时较长且无法及时对现场进行指导, 如果pH太高或太低都会影响离子浓度的测量结果。其他如离子色谱法、电感耦合离子质谱法等也存在测量误差大、周期长、无法实现自动在线测量等问题[5, 6]。为了避免这些问题, 迫切需要一种简单快速、价格低廉、适用于多种离子同时存在的水基钻井液离子浓度测量方法。离子选择电极法是一种更加灵活、高效的在线测量离子浓度的方法, 不受样本钻井液的色泽、混浊度、悬浮物或粘性的影响, 可以有效地检测出离子浓度, 而且这种方法的优势在于可以直接测量少量样本, 不需要进行任何破坏性的分析[7, 8], 具有设备简单、操作便捷、现场测定方便等优点, 而且不需要复杂的预处理步骤, 如稀释、过滤等, 可以最大程度地保持样本原始性质, 进而节省设备和维护成本[9, 10]。由于其响应速度极快（单次分析仅需1 min）, 电信号可直接放大采集, 可实现水基钻井液离子浓度自动化、连续测量, 且测量范围极广, 灵敏度极高, 通常可以达到多个数量级的浓度精度[11, 12]。

尽管传统离子选择电极在水基钻井液离子浓度测量中具有实时性和准确性优势, 但干扰离子的存在及相邻离子交错敏感性导致检测精度大幅下降, 严重影响了其在钻井液离子浓度测量中的应用。待测溶液的pH值对离子选择电极的定量分析有严重负面影响：既直接影响待测离子活度, 还会直接影响电极敏感膜的适用性, 一旦超出适用pH范围就会导致测定结果出现偏差, 从而直接影响测定精度。由能斯特方程可知, 离子选择电极电势值与温度常数有关, 而该常数又和离子选择电极的响应斜率有关, 如果温度发生变化, 那么离子选择电极的线性响应范围也会发生变化, 进而导致测量结果出现偏差。所以, 选择合适的温度和pH范围也是决定离子选择电极定量分析精度的重要因素。现场应用时, 水基钻井液的温度和pH值无法保持恒定, 因而本文通过实验分析建立补偿模型来改进能斯特测量模型, 去除温度和pH值对电极响应电位的影响, 构建离子选择电极的温度和pH补偿模型[13, 14, 15]。

1 离子选择电极测量原理

离子选择电极（IonSelectiveElectrode, 简称ISE）在原理上又被称作膜电极, 这是因为其结构中的敏感膜在测量过程中发挥着主要作用。

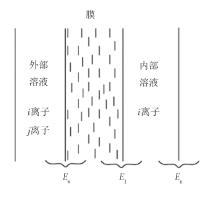
如图1所示, 当一片电化学膜将2个电解质溶液分隔开来时, 如果膜不会阻碍任何离子的通过, 而只是起到阻止2种电解质溶液快速混合的效果, 可移动的离子由浓度较高溶液向浓度较低的溶液扩散会产生一瞬间的通量, 带电荷的离子就会在膜两边形成电位差, 又称为液体接界电势。另一种情况, 如果电化学膜至少完全阻挡一类离子通过, 那么就会形成所谓的“ 唐南电势” 。

图1 电极电势模拟图

敏感膜是一种特殊的选择性透过膜, 它对不同离子的选择透过性只存在相对的大小而不会完全阻挡离子通过, 因此, 敏感膜的电势始终处于上述两种极端情况之间。

敏感膜只容许带有相同电荷的离子经过, 而不容许带有相反电荷的离子和溶剂分子经过, 所有离子通过膜选择性透过都为理想情况, 并且膜电流为零的前提下, 膜电势Em可以用统一的公式来表示：

Em=E0+RTziFlnai+∑j=1Najzi/zj（1）

式中：E0为初始电势; R为气体常数; T为绝对温度; F为法拉第常数; zi和zj为离子i与j的电荷数; ai为i离子在外部溶液中的浓度; aj为j离子在溶液中浓度。

公式（1）就是尼科尔斯基-艾森曼方程式, 是离子选择性电极分析中不可或缺的基础方程式。

如果电极能够有效地选择i离子, 则aj=0, 就能得到与能斯特公式完全一致的结果, 如公式（2）所示, 这也是工程上习惯于用能斯特关系来表述离子选择性电极响应特性的重要原因。

Em=E0+RTziFlnai（2）

离子选择电极是一种半电池, 它的电势不可独立测定, 而需要与外界参比电极结合构成一种整体的电化学电池, 以便测定电池的电动势, 这种电池的电势值可以通过多种方式来测定, 常用的方法如下：

E=Em+En-Ew-E1 （3）

式中：E为离子选择电极电势; En为内参比电极的电势; Ew与E1分别为外参比电极的电势及其液接部分的液接电势。

离子选择电极内部有一个内参比电极（通常为Ag/AgCl电极）, 浸没在内充液中。其作用是提供一个稳定的、不变的电势基准, 将膜电势传导到导线; 只要内充液的成分固定, 内参比电极电势就是恒定的。在测量时, 需要外参比电极（通常为甘汞电极或Ag/AgCl电极）浸入待测样品中, 以构成一个完整的电化学回路, 外参比电极电势同样提供一个稳定不变的电势基准, 其电势由电极自身的电对决定（如Hg2Cl2/Hg或AgCl/Ag）, 在标准条件下是已知且稳定的。液接电势为当两种不同成分或浓度的溶液接触时, 由于离子扩散速率不同, 在界面处会产生一个微小的电势差, 通常较小, 对测量精度影响不大。在正常的测量过程中, 上述三项参数可用一个常数项反映出来。

离子选择电极的量程很大, 可以达到多个数量级。按照膜电势的公式（1）, 用电势对离子浓度的对数作图, 可以得到一条直线, 其斜率为RT/ziF, 这便是标准曲线。然而, 当离子浓度较低时, 由于膜材料自身的溶解以及外界干扰离子的作用, 标准曲线出现明显的偏差。

2 离子选择电极pH补偿模型

待测溶液的pH值对离子选择电极定量分析有严重负面影响, 不仅会直接影响待测离子在待测溶液中的活度, 还会直接影响电极敏感膜的适用性, 如果超出适用的pH值范围就会导致特定离子的膜电势测定结果出现偏差, 从而直接影响测定精度。离子选择电极在实际测量流程中, 会受pH值变化的直接影响, 对待测离子的形态分布也可能产生影响, 同时, 由于电极对氢氧根离子（OH-）的电位响应, 也会导致测试结果出现偏差。因此, 选择合适的pH值是采用离子选择电极定量分析的关键。

2.1 pH补偿模型建立

经过前期研究, 根据柴佳丽等[16]提出的一种在能斯特方程式中导入基于多元线性回归的pH值线性补偿项的方法, 以此构建离子选择电极的pH补偿模型, 并将其表示为公式（4）-公式（6）：

Em=E0+2.303RTziFlgai（4）

将公式（4）代入到公式（3）可得：

E=E0+2.303RTziFlgai+En-E1-EW（5）

考虑到内参比电势、外参比电势、液接电势可用一个常数表示, 且离子选择电极经过常规实验测定后, 它们相互之间可以抵消, 因此公式（5）可以变换为下式：

E=E0+ωlgai（6）

式中：ω 为电极对离子浓度的响应斜率（ω =2.303RT/ziF）。

公式（6）中E0、ω 不是常数, 而是由多种环境因素决定的复合函数：

E= E0（ϕ 1, ϕ 2）+ω （ϕ 1, ϕ 2）lgai （7）

式中：（ϕ 1, ϕ 2）为环境因素。

假设其他外部因素恒定不变, 则pH值被视为影响离子选择电极电势的唯一环境变量, 因此：

E=E0+ω lgai+ω 0pH （8）

式中：ω 0为电极对OH-的响应斜率; pH为溶液的pH值。

2.2 实验仪器及实验设计

文中选用的电极测量范围以及适用的工作温度范围较广, 电极的适用条件较易实现, 能满足一般离子浓度测量需要, 可用于本文设计的离子浓度测量系统。氯离子电极标准参数如表1所示。分别选取5种不同氯离子浓度的溶液, 通过在溶液中加入不同量的酸、碱物质来调整溶液的pH值, 调整的pH参数值在2~12之间变化。实验过程中待测溶液的温度在5~45 ℃之间变化, 且每隔5 ℃进行一次实验采样, 从而实现氯离子浓度测量干扰因素的实验设计。

表1 氯离子电极标准参数
2.3 实验分析及数据处理

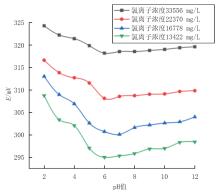
在恒定温度下, 选取磷酸作为调节待测溶液pH值的缓冲溶液, 分别调节浓度不同氯离子溶液的pH值, 并获得离子选择电极输出值, 观测被测溶液pH变化对氯离子电极输出值的影响, 结果如图2所示。保持氯离子浓度不变, 则电极的输出值随着pH值的变化而相应变化, 表明被测溶液pH值变化直接影响氯离子选择电极。

图2 不同pH时氯离子选择电极的输出曲线

图2的结果显示, 测得的氯离子浓度与pH值之间存在较好的相关性：当pH值在2.0~6.5范围内时, 氯离子电极测得的氯离子浓度会随着pH值的增加而降低; 当pH值在6.5~12.0范围内时, 氯离子浓度会随着pH值的增加而升高; 而当pH值达到6.5时, 电极的稳定性最佳。这表明OH-的存在会严重影响电极测量的准确性, 其与pH值之间的关系可以用下面的公式来表示。

EOH-=ω0pH+Em（9）

式中： EOH-为电极的响应电势。

利用图2中不同浓度梯度的氯离子溶液测定数据进行线性拟合, pH范围在2~6.5时, 得到pH对电极响应斜率为-1.212 mV/dec; pH范围在6.5~12时, 得到pH对电极响应斜率为0.232 5 mV/dec。将ω 0值作为pH的线性补偿系数代入公式（8）, 可得：

E=E0+ω lgai-1.212pH （10）

E=E0+ω lgai+0.2325pH （11）

2.4 模型验证及分析

为了验证模型的效果及准确性, 采用之前配制的氯离子的标准溶液改变其pH后进行测试, 其测量分析的结果如表2所示。

表2 不同pH值氯离子选择电极标准溶液的测定值与模型理论值对比分析

从表2可以看出, 经过pH补偿后测定氯离子的电势值最大相对误差为1.5%, 最小为0.8%, 相对误差保持在10%以内, 说明模型效果很好, 可以满足离子选择电极受pH影响的电势的补偿要求。该实验在25 ℃的室温中完成。

3 离子选择电极温度补偿模型

由能斯特方程可知, 离子选择电极的电势值与温度常数有关, 而温度常数又和离子选择电极的响应斜率有关, 如果温度发生变化, 那么离子选择电极的线性响应范围也会发生变化, 进而导致特定离子的膜电势测量结果出现偏差。所以, 温度影响的离子浓度误差补偿也是决定离子选择电极定量分析精度的重要因素。

3.1 温度补偿模型建立

如果在恒温条件下进行测量, 则根据能斯特方程得到公式（4）中的E0和电极斜率ω =2.303RT/ziF均保持不变, 输出电势值随待测离子浓度的对数值呈线性变化。如果在离子选择电极进行测量的过程中温度发生变化, 则输出电势值变为：

Em=E0（t）+ω （t）lgai （12）

令p=lgai, 则简化后的离子选择电极模型如下所示：

p=（a+bt）+（c+dt）Em （13）

假设x（t）、y（t）与温度t是线性关系, 令x（t）=a+bt, y（t）=c+dt, 则：

p=x（t）+y（t）Em （14）

式中：t为溶液温度; a、b、c、d为待定系数。

因此, 在离子选择电极的测量模型中, 以离子浓度为因变量, 输出电势和溶液温度为自变量。在一定温度下, 公式（13）中的p为离子浓度ai的对数, 与电极的输出电势呈线性关系; 随着温度的变化, 这种相关性可以表示为一系列直线, 其截距和斜率分别是温度的函数x（t）和y（t）。根据这个模型, 只需要测量电极的输出电势和溶液温度即可得到离子浓度。因此公式（13）是离子选择电极的温度补偿模型。

3.2 实验分析及数据处理

以氯离子选择电极为例, 配制4组标准溶液, 分别改变不同浓度溶液的温度, 保持pH不变, 采集输出离子电势值, 即可获得4组标准浓度下氯离子电极输出值和温度之间的关系, 如表3所示。

表3 溶液实际浓度与氯离子电极输出电势值及温度的关系

根据理论及实验研究, 将公式（13）转换为：

p=（a+bt）+（c+dt）Em=a+bt+cEm+dtEm （15）

记θ 1=（1, t, Em, tEm）, θ 2=（a, b, c, d）, 通过对不同时刻θ 1和θ 2的观测值进行估计, 并利用最小二乘法拟合, 能够得出以下结果：

a=-24.31444

b=1.06745

c=0.08022

d=-0.00339

故氯离子电极温度补偿模型为：

lgai=-24.31444+1.06745t+0.08022Em-0.00339tEm （16）

将上述公式进行变形后得到：

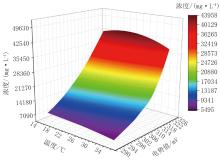
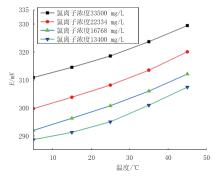
ai=10-24.31444+1.06745t+0.08022Em-0.00339tEm（17）

其测量模型三维视图如图3所示。氯离子电极测量模型可以准确地拟合样本, 对样本点的拟合如图4所示。

图3 氯离子测量模型三维视图

图4 不同温度时氯离子选择电极的输出

3.3 模型验证及分析

为了检验模型的效果和准确性, 测试不同浓度的标准溶液, 改变溶液的温度, 用离子选择电极测量输出电势值, 分析标准离子电势值和实际测量的电势值之间的相对误差值。测量分析结果如表4所示。

表4 不同温度下氯离子选择电极标准溶液测定值与模型理论值的对比分析

从表4可以看出, 温度补偿后氯离子测量的最大相对误差为6.58%, 最小为1.89%, 相对误差保持在10%以内, 表明该模型效果良好, 可以满足离子选择电极受温度影响的电势补偿要求。该实验在pH值为7的溶液环境中完成。

3.4 pH与温度综合补偿模型

利用公式（8）得到经过pH值校准之后的离子选择电极电势数值, 代入至公式（12）中的Em, 作为后续进行温度校准的离子选择电极电势, 并解算得到具体离子浓度。融合之后的公式如下所示：

E=E0（t）+ω （t）lgai+ω opH （18）

通过结合pH值的具体校准模型（10）（11）以及温度的校准模型（16）, 进行整合得到最终的离子选择电极校准模型, 如下所示。

lgai=-24.31444+1.06745t+0.08022（E-1.212pH）-0.00339t（E-1.212pH）（2pH6.5）lgai=-24.31444+1.06745t+0.08022（E+0.2325pH）-0.00339t（E+0.2325pH）（6.5≤pH12）（19）

4 现场验证

为了验证离子浓度校准模型的有效性, 将集成校准模型的钻井液氯离子浓度测量模块在X 1井水基钻井液中现场应用测试。将水基钻井液离子浓度自动化测量系统获得的数据与现场滴定的数据进行对比, 结果如表5所示。氯离子浓度测量的最大相对误差仅为6.68%, 可以满足现场水基钻井液离子浓度的测量要求。

表5 氯离子浓度测试数据

从总体应用结果来看, 水基钻井液离子浓度自动化测量系统在常规水基钻井液中应用时, 有较好的精度, 总体误差小于10%, 可以满足现场的应用要求。

5 结论

本文介绍了基于能斯特方程的线性pH补偿和温度补偿, 针对离子选择电极测量受pH和溶液温度影响的问题建立了补偿模型。实验结果表明：经过pH补偿后测定氯离子电势值的最大相对误差为1.5%, 最小相对误差为0.8%; 温度补偿后氯离子测量的电势值最大相对误差为6.58%, 最小为1.89%, 相对误差均保持在10%以内, 该补偿模型能有效消除测量过程中pH值和溶液温度的影响, 一定程度上提高了检测精度。通过结合使用两个补偿模型, 并进行现场实际测试显示, 氯离子浓度测量的最大相对误差仅为6.68%, 可以满足现场水基钻井液离子浓度的测量要求。

（编辑 郑春生）

参考文献
[1] 徐梦媛. 油基钻井液固井冲洗液配方研发及综合评价体系构建[D]. 西安: 西安建筑科技大学, 2021.
XU Mengyuan. Development of oil-based drilling fluid cementing spacer formulation and construction of comprehensive evaluation system[D]. Xi'an: Xi'an University of Architecture and Technology, 2021. [本文引用:1]
[2] 王守宴. 钻井过程中钻井液漏失及溢流的判断[J]. 西部探矿工程, 2020, 32(8): 49-52.
WANG Shouyan. Judgment of drilling fluid loss and kick during drilling process[J]. West-China Exploration Engineering, 2020, 32(8): 49-52. [本文引用:1]
[3] 田径. 钻遇盐膏层高压盐水的井控技术[D]. 成都: 西南石油大学, 2012.
TIAN Jing. Well Control Technology for drilling into high-pressure brine in salt-gypsum layers[D]. Chengdu: Southwest Petroleum University, 2012. [本文引用:1]
[4] 付顺龙. 钻井液常见污染问题分析及处理措施[J]. 中国石油和化工标准与质量, 2021, 41(12): 27-28.
FU Shunlong. Analysis of common contamination problems in drilling fluid and their treatment measures[J]. China Petroleum and Chemical Stand ard and Quality, 2021, 41(12): 27-28. [本文引用:1]
[5] 姚伦炳, 陈莲柳. 钻井液及其滤液中氯离子浓度的测定: 硝酸汞-二苯卡巴腙滴定法[J]. 油田化学, 1987(3): 43-48.
YAO Lunbing, CHEN Lianliu. Determination of chloride ion concentration in drilling fluid and Its Filtrate: Mercury nitrate-diphenylcarbazone titration method[J]. Oilfield Chemistry, 1987(3): 43-48. [本文引用:1]
[6] MAHAJAN R K, PURI R K, MARWAHA A, et al. Highly selective potentiometric determination of mercury(Ⅱ) ions using 1-furan-2-yl-4-(4-nitrophenyl)-2-phenyl-5H-imidazole-3-oxide based membrane electrodes[J]. Journal of Hazardous Materials, 2009, 167(1-3): 237-243. [本文引用:1]
[7] BUJES-GARRIDO J, ARCOS-MARTINEZ M J. Disposable sensor for electrochemical determination of chloride ions[J]. Talanta, 2016, 155: 153-157. [本文引用:1]
[8] KALISZ J, WEGRZYN K, MICHALSKA A, et al. Resolution increase of ion-selective electrodes response by using a reversed amperometric setup[J]. Electrochimica Acta, 2022, 427: 140886. [本文引用:1]
[9] SANAVI KHOSHNOOD R, AKBARI S, MASHAYEKHI CHENARBOU T. Determination of Aluminium by potentiometry using carbon paste ion selective electrode based on N, N'-bis (salicylidene)-1, 3-propanediamine ligand [J]. Journal of Analytical Chemistry, 2022, 77(8): 1057-1061. [本文引用:1]
[10] 方仲农. 离子色谱法测定工作场所中低浓度硝酸根的研究[J]. 广东化工, 2022, 49(23): 244-246, 232.
FANG Zhongnong. Study on determination of low-concentration nitrate in workplace by Ion Chromatography[J]. Guangdong Chemical Industry, 2022, 49(23): 244-246, 232. [本文引用:1]
[11] 王雅琳. 离子选择电极在化工分析检测中的应用[J]. 化工管理, 2022(2): 25-28.
WANG Yalin. Application of ion-selective electrodes in chemical analysis and detection[J]. Chemical Enterprise Management, 2022(2): 25-28. [本文引用:1]
[12] 金衍健, 应忠真, 朱剑, 等. 硝酸银滴定法测定废水中氯离子含量[J]. 山东化工, 2020, 49(19): 87-89.
JIN Yanjian, YING Zhongzhen, ZHU Jian, et al. Determination of chloride Ion content in waste water by silver nitrate titration method[J]. Shand ong Chemical Industry, 2020, 49(19): 87-89. [本文引用:1]
[13] 刘新敏, 侯捷, 李睿, 等. 应用离子选择电极直接测定离子浓度的迭代运算法[J]. 西南大学学报(自然科学版), 2010, 32(11): 124-129.
LIU Xinmin, HOU Jie, LI Rui, et al. Iterative algorithm for direct determination of ion concentration using ion selective electrodes[J]. Journal of Southwest University (Natural Science Edition), 2010, 32(11): 124-129. [本文引用:1]
[14] 郝栗涛, 雒昆利, 张湜溪, 等. 离子选择电极法测定天然水中氯离子含量[J]. 检验检疫学刊, 2019, 29(1): 25-28.
HAO Litao, LUO Kunli, ZHANG Shixi, et al. Determination of chloride ion content in natural water by ion selective electrodes Method[J]. Journal of Inspection and Quarantine, 2019, 29(1): 25-28. [本文引用:1]
[15] 周智, 苏小光, 李明, 等. 液相/气相条件漏斗型双电极氯离子浓度检测方法[J]. 传感器与微系统, 2021, 40(12): 149-152.
ZHOU Zhi, SU Xiaoguang, LI Ming, et al. Funnel-type dual-electrode chloride ion concentration detection method in liquid/gas phase conditions[J]. Transducer and Microsystem Technologies, 2021, 40(12): 149-152. [本文引用:1]
[16] 柴佳丽, 马剑琪. 以电极电势书写能斯特方程[J]. 化工设计通讯, 2020, 46(9): 140-142.
CHAI Jiali, MA Jianqi. Writing nernst equation with electrode potential[J]. Chemical Engineering Design Communications, 2020, 46(9): 140-142. [本文引用:1]