引用本文
范伟, 孙红华, 杨丹, 窦松江, 程兴春, 马丽杰. 基于CNN-LSTM混合神经网络的储层孔隙度预测模型构建及应用[J]. 录井工程, 2025,36(4): 13-20.
FAN Wei, SUN Honghua, YANG Dan, DOU Songjiang, CHENG Xingchun, MA Lijie. Construction and application of a reservoir porosity prediction model based on CNN-LSTM hybrid neural network[J]. Mud Logging Engineering, 2025,36(4): 13-20.
Doi:10.3969/j.issn.1672-9803.2025.04.003  
Permissions
Copyright©2025, 《录井工程》杂志社
《录井工程》杂志社 所有
基于CNN-LSTM混合神经网络的储层孔隙度预测模型构建及应用
范伟①, 孙红华①, 杨丹②, 窦松江③, 程兴春①, 马丽杰①
①中国石油渤海钻探第二录井公司
②中国石油大港油田公司勘探事业部/地球物理部
③中国石油大港油田公司勘探开发研究院

作者简介：范伟 工程师,1986年生,2010年毕业于西安石油大学信息管理与信息系统专业,现在中国石油渤海钻探第二录井公司从事现场地质工程一体化工作。通信地址：062550 河北省任丘市渤海钻探第二录井公司。E-mail：fan_wei@cnpc.com.cn

收稿日期: 2025-11-14
摘要

多元线性回归等传统的储层孔隙度预测方法,通常难以有效捕捉测井数据的时空特征及掌握测井数据与孔隙度间复杂的非线性关系,导致预测结果与实测数据间存在较大误差。为此,引入卷积神经网络（CNN）-长短期记忆网络（LSTM）混合神经网络方法,阐述基于测井数据的CNN-LSTM混合神经网络储层孔隙度预测原理,采用互信息法筛选出与孔隙度相关性较强的声波时差、体积密度、补偿中子和自然伽马4个测井参数作为模型输入特征,构建CNN-LSTM混合神经网络模型的预测流程,选取样本数据并划分训练集及测试集,通过缺失值处理、标准化和数据重塑对样本数据进行处理,最终建立了基于测井数据与储层孔隙度间非线性映射关系的孔隙度预测模型。模型的测试和评估结果表明：该混合神经网络模型在同井预测的误差指标 MAE和 RMSE分别降至0.2和0.25以下,比多元线性回归模型低60%以上,比循环神经网络模型低50%以上,比长短期记忆网络模型低40%以上。在未参与训练的C井的现场应用中,预测精度达到92.3%,应用效果良好。

关键词: 储层解释; 孔隙度预测; 测井资料; CNN-LSTM; 混合神经网络; 互信息
中图分类号:TE132.1 文献标志码:A
Construction and application of a reservoir porosity prediction model based on CNN-LSTM hybrid neural network
FAN Wei①, SUN Honghua①, YANG Dan②, DOU Songjiang③, CHENG Xingchun①, MA Lijie①
①No.2 Mud Logging Company, BHDC, CNPC, Renqiu, Hebei 062550, China
②Exploration Division/Geophysical Department, PetroChina Dagang Oilfield Company, Tianjin 300280, China
③Exploration and Development Research Institute, PetroChina Dagang Oilfield Company, Tianjin 300280, China
Abstract

Traditional reservoir porosity prediction methods, such as multiple linear regression, are usually difficult to capture the spatial-temporal characteristics of logging data and to grasp the complex nonlinear relationship between logging data and porosity, resulting in greater errors between predicted results and measured data. To address this, a hybrid neural network method of Convolutional Neural Network （CNN）-Long Short-Term Memory （LSTM） is introduced to expound the reservoir porosity prediction principle of CNN-LSTM hybrid neural network based on logging data. Four logging parameters with strong correlation to porosity, namely interval transit time, volume density, compensated neutron and natural gamma, were selected by mutual information method screening as the input features of the model to construct the prediction process of the CNN-LSTM hybrid neural network model. Sample data were selected and divided into train and test sets. The sample data were processed through missing value handling, standardization, and data reshaping, ultimately establishing a porosity prediction model based on the nonlinear mapping relationship between logging data and reservoir porosity. The test and assessment results of the model show that the hybrid neural network model reduces the error indices MAE and RMSE in the same well prediction to below 0.2 and 0.25 respectively, representing more than 60% lower than multiple linear regression model, more than 50% lower than recurrent neural network model, and more than 40% lower than long short-term memory network model.In the field application of well C that did not participate in training, the prediction accuracy reached 92.3%, and the application effect was good.

Keyword: reservoir interpretation; porosity prediction; logging data; CNN-LSTM; hybrid neural network; mutual information
0 引言

储层孔隙度是油气地质勘探与开发中的重要参数[1, 2], 能够直接影响储层的油气储集能力与流体流动特性, 对资源的有效评估与开发至关重要。因此, 实现储层孔隙度的精确预测对于进行储层评价及油气田经济高效开发具有重要作用[3, 4]。测井技术是地球物理测井技术的简称, 是储层开发过程中获取地层信息的有效手段。常规的储层孔隙度预测方法主要依赖于测井数据与孔隙度之间的线性回归关系, 如多元线性回归等, 然而线性回归存在以下两方面局限性：一是该方法通常依赖储层孔隙度与测井数据之间的线性关系, 对于复杂储层的孔隙度预测精度较低; 二是该方法通常无法有效捕捉测井数据局部空间特征以及孔隙度随深度变化的复杂时序特性, 导致在空间、时序变化显著的储层中, 预测误差达不到工程需求[5, 6]。鉴于此, 针对储层复杂非线性空间关系和时序变化, 亟需探索更为精准的储层孔隙度预测方法以满足实际需求。

近年来, 国内外学者基于测井资料预测储层孔隙度的研究已取得重要进展。崔学慧等[7]基于地层声波时差、自然电位、自然伽马及电阻率4种测井曲线, 采用随机森林（RF）回归算法建立了孔隙度预测模型, 其精度远高于线性回归预测。杨柳青等[8]提出基于卷积神经网络的储层物性参数预测方法, 融合地震数据和测井数据实现了储层孔隙度的预测。檀朝东等[9]提出基于深度强化学习的储层物性参数预测方法, 使用强化学习算法优化深度学习模型的结构和参数。侯贤沐等[10]采用长短期记忆网络（LSTM）方法, 通过测井数据对碳酸盐岩储层的孔隙度和渗透率进行了预测。Kalule R等[11]采用堆叠深度学习方法, 通过结合多个机器学习和深度学习模型的预测结果, 提高了碳酸盐岩孔隙度和绝对渗透率的预测精度。

尽管现有研究在基于测井数据的储层孔隙度预测领域已取得显著进展, 但仍存在一定的局限性：一是多数研究集中于单一神经网络的预测模型, 难以有效处理测井数据的时空特性; 二是多数方法仍局限于对测井数据的局部特征提取, 忽视了长时间序列特征对储层孔隙度预测的影响[12, 13, 14]。针对上述问题, 笔者提出了一种基于卷积神经网络（CNN）-长短期记忆网络（LSTM）混合神经网络的储层孔隙度预测模型, 结合CNN在空间特征提取和LSTM在时序数据处理方面的优势, 同时捕捉孔隙度与测井数据间的非线性时空关联, 提高预测精度, 为储层孔隙度的预测提供了一种新的思路[15, 16]。

1 CNN-LSTM储层孔隙度预测模型原理
1.1 CNN-LSTM混合神经网络简介

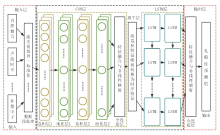
CNN-LSTM混合神经网络模型是一种结合了卷积神经网络（CNN）和长短期记忆网络（LSTM）的深度学习模型, 主要用于处理具有空间和时间特征的复杂预测任务[17, 18]。该模型通过整合CNN和LSTM的优势, 构建了一个强大的混合神经网络架构：CNN能够有效提取输入数据的局部序列特征, LSTM则能有效捕捉时间序列数据中的长期依赖关系, 进而建立不同深度点之间的动态关联。这种组合架构使其适用于储层孔隙度预测等需要综合分析时空动态的任务[19, 20, 21], CNN-LSTM混合神经网络模型包括输入层、CNN层、展平层、LSTM层和输出层, 结构如图1所示。

图1 CNN-LSTM混合神经网络模型结构

1.2 CNN-LSTM混合神经网络模型各层功能

CNN-LSTM混合神经网络模型通过建立测井参数与储层孔隙度之间的非线性映射实现孔隙度的预测。其各层功能描述如下：①输入层将完成预处理的测井数据作为预测模型的输入; ②CNN层通过一维卷积核对测井数据序列进行卷积操作, 提取深度方向上的局部特征, 并通过池化层对特征图进行降维并保留关键信息, 然后通过全连接层对卷积提取的空间特征进行融合与降维, 将局部特征映射为更紧凑的特征向量, 为后续的序列建模提供高效输入; ③展平层将CNN层输出的多维特征图展开为一维向量, 实现空间特征到时序特征输入的结构转换; ④LSTM层接收展平层输出的特征序列, 通过两层LSTM结构捕捉深度序列中的时序依赖关系, 提炼出与储层孔隙度相关的时序特征; ⑤输出层在接收LSTM层输出结果的基础上, 通过全连接层进行特征融合与非线性映射, 实现对提取特征的加权映射, 通过激活函数生成储层孔隙度的最终预测值[22, 23, 24, 25]。

2 储层孔隙度预测模型的构建
2.1 模型输入特征选取

在构建CNN-LSTM混合神经网络模型以预测地层孔隙度的过程中, 输入特征的选择对模型的预测性能具有重要影响。为确保输入变量与目标变量之间具有较强的相关性, 本文采用互信息（Mutual Information, MI）法对测井参数进行特征筛选。互信息法能够同时刻画变量之间的线性与非线性依赖关系, 相较于传统的皮尔逊相关系数等线性度量方法, 其在处理复杂地质参数关系时具有更高的适用性与鲁棒性。

首先, 收集测井参数与孔隙度实测数据, 设输入特征集合为X={X1, X2, X3, X4, X5}={AC, DEN, GR, CNL, RT}（其中AC为声波时差、DEN为体积密度、GR为自然伽马、CNL为补偿中子、RT为地层电阻率）, 目标变量为孔隙度。为消除不同量纲及量级差异对计算结果的影响, 对所有特征变量与目标变量进行归一化或标准化处理。

互信息用于衡量两个随机变量X与Y之间的统计依赖程度, 当X与Y（目标变量）相互独立时, 互信息值为0; 互信息值越大, 说明二者的依赖关系越强, 即该特征对目标变量的信息贡献越大。互信息值计算公式如下：

$I(X ; Y)=\sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)}$ （1）

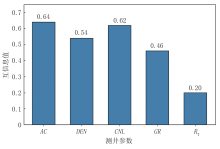
式中：I（X; Y）为互信息值; p（x，y）为X与Y的联合概率分布; p（x）和p（y）分别为X与Y的边缘概率分布。

由于测井参数与孔隙度均为连续型变量, 可采用基于k近邻非参数估计方法的互信息计算方式, 通过局部邻域统计实现联合概率与边缘概率的估计, 获得每个测井参数与孔隙度之间的互信息值。根据测井参数互信息值计算结果（图2）可见, 声波时差、体积密度、补偿中子和自然伽马4个参数与孔隙度的互信息值较高, 表明其与目标变量存在较强的相关性。结合地质意义与互信息值分析结果, 最终选择上述4个参数作为CNN-LSTM模型的输入特征, 为后续提高模型在孔隙度预测任务中的泛化能力与预测精度提供了更加合理的输入基础, 有效保留了对目标变量具有显著解释能力的特征信息。

图2 测井参数互信息值计算结果

2.2 模型预测流程

在完成输入特征的选取后, 构建基于CNN-LSTM混合神经网络的储层孔隙度预测模型, 实现由测井数据到孔隙度的非线性映射预测, 具体预测流程如下。

（1）将经过数据预处理的声波时差、体积密度等4项测井参数序列输入至卷积神经网络（CNN）层。CNN层通过卷积核在深度方向滑动, 对测井数据进行局部特征提取, 能够有效识别地层参数的空间变化模式。同时, 通过池化操作对特征图进行降维, 保留关键空间特征并减少计算量。

（2）CNN层输出的特征序列经展平层后输入至长短期记忆网络（LSTM）层。LSTM层通过门控机制（输入门、遗忘门和输出门）对时间序列特征进行建模, 捕捉地层测井数据在深度方向上的时序依赖关系, 从而提取与孔隙度变化密切相关的动态特征。

（3）将LSTM层提取的高阶时序特征输入全连接层, 由其对空间与时序特征进行整合与非线性变换, 最终生成储层孔隙度的预测值。

在模型训练过程中, 为确保训练的稳定性与预测效果, 选取合适的激活函数、损失函数及优化器, 并通过回调函数对训练过程进行动态优化; 同时采用早停法与学习率衰减策略, 以提升模型的收敛效率与泛化性能。该预测流程充分发挥了CNN在空间特征提取方面的优势与LSTM在时序建模方面的能力, 使CNN-LSTM混合神经网络模型能够更准确地刻画测井数据与储层孔隙度之间的复杂非线性关系, 得到更高的储层孔隙度预测精度。

3 样本数据处理与模型测试评估
3.1 样本数据选取

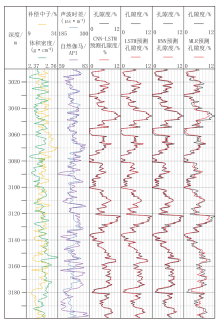
选取西南某探区地质条件相对近似、测井参数特征相近的A井和B井作为研究对象, 两口井的研究井段分别为2 075~2 940 m和2 250~3 200 m。两口井均包含声波时差、自然伽马、补偿中子和体积密度4条测井曲线。为了评估所构建混合神经网络模型的精度, 同步采用其他模型开展了对比实验。在A井和B井中, 均选择80%的数据作为训练集, 20%的数据作为测试集, 详细的样本数据集划分如表1所示。

表1 样本数据集划分
3.2 样本数据处理

在完成样本数据集划分后, 对样本数据进行预处理, 其中包括缺失值处理、标准化和数据重塑, 以确保模型输入数据的一致性。

（1）采用线性插值法来填充训练集的缺失值, 其计算公式如下：

ymissing=yi+（yj-yi）（xmissing-xi）xj-xi（2）

式中： ymissing为缺失值; yi、yj为相邻非缺失数据点; xi、xj为yi与yj对应的深度值; xmissing为缺失点对应的深度值。

（2）为消除不同测井参数在数值范围和量纲上的差异, 避免特征尺度不一致对模型训练产生影响, 对输入特征进行标准化处理。经标准化后, 各输入变量在模型训练中具有相同的数值尺度, 有助于提高模型的收敛效率与稳定性。本文采用z-score标准化方法, 将各测井参数转换为零均值、单位方差的分布形式, 计算公式如下：

z'=z-μσ（3）

式中： z'为标准化后的特征值; z为原始特征值; μ为该特征的均值; σ为标准差。

（3）为满足CNN-LSTM模型的输入结构要求, 对预处理后的样本数据进行数据重塑, 将连续测井数据按照深度方向划分为固定长度的样本窗口, 并重塑为三维张量形式。此过程保证了数据在样本、时间及特征维度上的一致性, 使CNN层能够提取空间局部特征, 而LSTM层能够捕捉深度方向的时序依赖关系, 从而提升孔隙度预测的精度与鲁棒性。其计算公式如下：

u∈RN×T×F（4）

式中：u为输入样本数据的张量表示; R为实数域; N为样本数量; T为时间步长（或深度窗口长度）; F为每个样本的特征数。

3.3 模型参数设置

基于CNN-LSTM混合神经网络的储层孔隙度预测模型是含有两层CNN和两层LSTM的混合架构, 通过联合全连接层完成孔隙度的端到端预测。该模型以经过预处理的测井数据作为输入, 以孔隙度预测结果作为输出。CNN层通过一维卷积核提取测井数据的局部特征, LSTM层捕捉深度序列的时序依赖, 全连接层整合特征并输出最终预测结果。CNN-LSTM混合神经网络储层孔隙度预测模型的具体参数配置如下：输入层设置4个输入特征; CNN 层由2个卷积层构成, 每层均配置64个卷积核, 激活函数选用ReLU（线性整流函数）, 同时设置0.2的Dropout（随机失活）率, 并采用MaxPooling1D（一维最大池化）的池化方式; LSTM层包含2层网络层, 每层设置50个神经元, 激活函数采用tanh（双曲正切函数）, Dropout（随机失活）率设定为0.3; 全连接层依次配置128、64个神经元; 最终通过单输出层输出孔隙度预测结果。在模型训练超参数配置层面, 优化器选用 Adam（自适应矩估计优化器）, 损失函数采用均方误差（MSE）; 同时将学习率衰减因子、时间步长及早停耐心值分别设定为 0.2、5 和 10。

激活函数是神经网络中引入非线性映射关系的关键组成部分, 它决定了神经元对输入信号的响应形式, 对模型的特征提取能力和训练稳定性具有重要影响。模型中采用的ReLU函数与tanh函数在不同层中发挥互补作用。

ReLU函数、tanh函数的表达式分别如下：

$f(x)=\max (0, x)$（5）

$f(x)=\tanh (x)=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}}$（6）

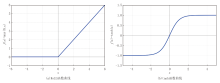
ReLU函数曲线如图3a所示, 该函数在输入为正时保持线性输出, 在输入为负时输出0, 这有效避免了梯度消失问题, 进而增强了CNN层对测井曲线局部非线性特征的提取能力。tanh函数曲线如图3b所示, 该函数将输入值映射至 [-1，1区间, 具有良好的平滑性与对称性, 有助于LSTM单元在时间序列建模中保持信息的连续传递与稳定更新, 防止数值在长序列传播中出现过度放大或衰减。

图3 CNN-LSTM混合神经网络模型函数曲线

通过结合ReLU函数和tanh函数, 本模型能够在时序数据中同时提取空间特征和时间特征, 显著提高了孔隙度预测的准确性。

3.4 模型测试

分别将A井和B井的训练与测试样本数据集输入CNN-LSTM混合神经网络模型中, 进行储层孔隙度预测。为展现CNN-LSTM模型的预测精度, 将该模型的预测结果与多元线性回归（MLR）、循环神经网络（RNN）和长短期记忆网络（LSTM）模型的预测结果进行了比较。A井和B井的测试集孔隙度预测结果对比分别如图4和图5所示。

图4 A井测试集4种模型的预测结果

图5 B井测试集4种模型的预测结果

预测结果表明, CNN-LSTM模型在预测精度上优于LSTM、RNN和MLR模型。CNN-LSTM模型能够更准确地捕捉数据的细微变化, 特别是在复杂的储层区段; 相比之下LSTM模型的预测结果出现了一些波动, 难以精准捕捉测井数据中的局部空间特征; 尽管RNN模型能够较好地捕捉时序特征, 但其在处理地层中复杂时空关系时表现不及LSTM模型, 并且无法像CNN-LSTM模型那样有效地提取空间特征, 导致其孔隙度预测精度低于二者; 而MLR模型存在较大的偏差, 无法准确反映测井参数变化对孔隙度的影响。总体而言, CNN-LSTM模型在两口井不同深度区间的孔隙度预测中均表现更加精准, 明显优于LSTM、RNN和MLR模型。

3.5 模型评估

为了全面评估所构建模型的预测精度, 选择了均方根误差（RMSE）和平均绝对误差（MAE）作为评价指标进行分析, 二者的值越低, 表明模型预测精度越高。RMSE和MAE的计算公式如下：

RMSE=1N∑i=1N（yi-ŷi）2（7）

MAE=1N∑i=1Nyi-ŷi（8）

式中：RMSE为均方根误差; MAE为平均绝对误差; yi为实际值; ŷi为预测值; N为样本总数。

CNN-LSTM、LSTM、RNN、MLR模型的预测误差如表2所示。从表中可看出, 在RMSE和MAE评价指标下, CNN-LSTM模型的预测精度最佳, 优于其他3种模型。特别是CNN-LSTM模型对A井预测的RMSE和MAE指标, 分别比LSTM模型低约50.01%和54.14%, 比RNN模型低约58.47%和60.10%, 比MLR模型低约70.70%和75.19%; 对B井预测的RMSE和MAE指标, 分别比LSTM模型低约47.50%和42.97%, 比RNN模型低约54.44%和53.68%, 比MLR模型低约70.74%和69.99%。分析结果表明, CNN-LSTM模型在储层孔隙度预测方面的应用效果良好。

表2 不同模型的预测误差

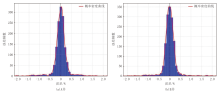
为了进一步验证CNN-LSTM模型的预测精度, 使用直方图直观展示A、B井测试集的预测孔隙度与实际孔隙度之间误差的分布（图6）。从误差分布图可知, 预测误差主要集中于-0.5%~0.5%的区间内, 呈近似正态分布的特征, 概率密度曲线在0处达到峰值, 表明预测值与实际值之间的偏差在大多数样本中较小。误差分布的集中性反映了CNN-LSTM模型对两口井预测孔隙度的高精度, 而分布的对称性则表明模型预测不存在显著的系统性偏差, 整体预测精度稳定, 验证了其在储层孔隙度预测中的适用性和可靠性。

图6 A、B井测试集误差分布直方图

4 模型应用效果

为进一步验证所构建CNN-LSTM混合神经网络储层孔隙度预测模型的泛化能力与跨井适用性, 利用A、B井的测井数据联合训练模型, 以充分学习不同井段的测井响应特征与孔隙度之间的非线性关系, 从而提升模型对地层非均质性的适应能力。

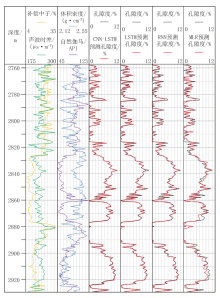
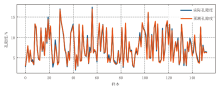
训练完成后, 将模型应用于C井的孔隙度预测, C井未参与模型训练, 作为独立测试集用于验证模型的泛化性能。C井与A、B井同属一个探区, 在其测深2 450~2 900 m井段选取样本数量155组, 测井曲线类型与训练井保持一致, 模型在C井上的预测应用结果如图7所示。

图7 CNN-LSTM模型在C井上的预测应用结果

由图7可以看出, CNN-LSTM模型能够较好地捕捉C井孔隙度的整体变化趋势, 预测曲线与实测曲线在主干趋势及峰谷位置上具有较高一致性。尽管在局部薄层或高非均质区间存在一定偏差, 但整体误差较小, 说明模型具备较强的跨井推广能力。定量评估的结果表明：模型在C井上的RMSE为0.326 3, MAE为0.233 2, 预测精度为92.3%。与A、B井训练测试的预测结果相比, 误差指标略有增加, 但仍能保持较高的预测精度与稳定性, 验证了基于多井联合训练的CNN-LSTM模型用于未知井数据的有效性与泛化能力。

5 结论

（1）多元线性回归等传统基于测井数据的储层孔隙度预测方法, 通常难以有效捕捉测井数据的时空特征及测井数据与孔隙度复杂的非线性关系, 导致预测结果常与实际孔隙度间存在较大误差。针对这一问题, 引入CNN-LSTM混合神经网络方法, 建立基于测井数据的储层孔隙度非线性时空关联预测模型。

（2）CNN-LSTM模型在A、B井的测试评估结果表明, 其预测误差显著低于传统的LSTM、RNN和MLR模型。CNN-LSTM模型对A、B井孔隙度预测的RMSE和MAE指标分别比LSTM模型低40%以上, 比RNN模型低50%以上, 比MLR模型低60%以上。

（3）CNN-LSTM模型经A、B井训练后, 跨井应用于C井孔隙度预测, 预测精度达到92.3%。实验结果验证了CNN-LSTM模型能够有效提高孔隙度预测精度, 满足工程需求。

（编辑 唐艳军）

参考文献
[1] 安鹏, 曹丹平, 赵宝银, 等. 基于LSTM循环神经网络的储层物性参数预测方法研究[J]. 地球物理学进展, 2019, 34(5): 1849-1858.
AN Peng, CAO Danping, ZHAO Baoyin, et al. Reservoir physical parameters prediction based on LSTM recurrent neural network[J]. Progress in Geophysics, 2019, 34(5): 1849-1858. [本文引用:1]
[2] 段燕玲. 现代测井技术在油田开发中的应用研究[J]. 石化技术, 2025, 32(1): 272-274.
DUAN Yanling. Study on the application of modern well logging technology in oilfield development[J]. Petrochemical Industry Technology, 2025, 32(1): 272-274. [本文引用:1]
[3] 李奎周, 王团, 赵海波, 等. 基于深度前馈神经网络的致密砂岩储层孔隙度预测[J]. 大庆石油地质与开发, 2023, 42(5): 140-146.
LI Kuizhou, WANG Tuan, ZHAO Haibo, et al. Porosity prediction of tight sand stone reservoir based on deep feedforward neural network[J]. Petroleum Geology & Oilfield Development in Daqing, 2023, 42(5): 140-146. [本文引用:1]
[4] 张宇航, 时保宏, 张曰静, 等. 机器学习方法在浅层滩坝相薄储层孔隙度预测中的应用: 以准噶尔盆地车排子地区白垩系为例[J]. 沉积学报, 2023, 41(5): 1559-1567.
ZHANG Yuhang, SHI Baohong, ZHANG Yuejing, et al. Application of machine learning for porosity estimation of beach and bar sand bodies in a lacustrine basin: A case study of the Lower Cretaceous strata in Chepaizi area, Junggar Basin, NW China[J]. Acta Sedimentologica Sinica, 2023, 41(5): 1559-1567. [本文引用:1]
[5] 陈康, 狄贵东, 张佳佳, 等. 基于改进U-Net卷积神经网络的储层预测[J]. CT理论与应用研究, 2021, 30(4): 403-415.
CHEN Kang, DI Guidong, ZHANG Jiajia, et al. Reservoir prediction based on improved U-net Convolutional Neural Network[J]. CT Theory and Application, 2021, 30(4): 403-415. [本文引用:1]
[6] MANSOOR M I, TUAMA H M, HUMAIDI A J. Application of correlation-based recurrent neural network in porosity prediction for petroleum exploration[J]. Engineering Research Express, 2025, 7(1): 15241. [本文引用:1]
[7] 崔学慧, 刘长江, 薛亮, 等. 基于随机森林回归算法预测孔隙度的研究[J]. 西部探矿工程, 2019, 31(11): 99-102, 105.
CUI Xuehui, LIU Changjiang, XUE Liang, et al. Study on predicting porosity based on rand om forest regression algorithm[J]. West-China Exploration Engineering, 2019, 31(11): 99-102, 105. [本文引用:1]
[8] 杨柳青, 陈伟, 查蓓. 利用卷积神经网络对储层孔隙度的预测研究与应用[J]. 地球物理学进展, 2019, 34(4): 1548-1555.
YANG Liuqing, CHEN Wei, ZHA Bei. Prediction and application of reservoir porosity by convolutional neural network[J]. Progress in Geophysics, 2019, 34(4): 1548-1555. [本文引用:1]
[9] 檀朝东, 蔡振华, 邓涵文, 等. 基于强化学习的煤层气井螺杆泵排采参数智能决策[J]. 石油钻采工艺, 2020, 42(1): 62-69.
TAN Chaodong, CAI Zhenhua, DENG Hanwen, et al. Intelligent decision making on PCP production parameters of CBM wells based on reinforcement learning[J]. Oil Drilling & Production Technology, 2020, 42(1): 62-69. [本文引用:1]
[10] 侯贤沐, 王付勇, 宰芸, 等. 基于机器学习和测井数据的碳酸盐岩孔隙度与渗透率预测[J]. 吉林大学学报(地球科学版), 2022, 52(2): 644-653.
HOU Xianmu, WANG Fuyong, ZAI Yun, et al. Prediction of carbonate porosity and permeability based on machine learning and logging data[J]. Journal of Jilin University (Earth Science Edition), 2022, 52(2): 644-653. [本文引用:1]
[11] KALULE R, ABDERRAHMANE H A, ALAMERI W, et al. Stacked ensemble machine learning for porosity and absolute permeability prediction of carbonate rock plugs[J]. Scientific Reports, 2023, 13(1): 9855. [本文引用:1]
[12] 程希, 程宇雪, 程佳豪, 等. 基于机器学习与大数据技术的地球物理测井系统[J]. 西安石油大学学报(自然科学版), 2019, 34(6): 108-116.
CHENG Xi, CHENG Yuxue, CHENG Jiahao, et al. Geophysical logging system based on machine learning and big data technology[J]. Journal of Xi′an Shiyou University(Natural Science Edition), 2019, 34(6): 108-116. [本文引用:1]
[13] 段友祥, 李根田, 孙歧峰. 卷积神经网络在储层预测中的应用研究[J]. 通信学报, 2016, 37(增刊1): 1-9.
DUAN Youxiang, LI Gentian, SUN Qifeng. Research on convolutional neural network for reservoir parameter prediction[J]. Journal on Communications, 2016, 37(S1): 1-9. [本文引用:1]
[14] 史长林, 魏莉, 张剑, 等. 基于机器学习的储层预测方法[J]. 油气地质与采收率, 2022, 29(1): 90-97.
SHI Changlin, WEI Li, ZHANG Jian, et al. Reservoir prediction method based on machine learning[J]. Petroleum Geology and Recovery Efficiency, 2022, 29(1): 90-97. [本文引用:1]
[15] ONALO D, OLORUNTOBI O, ADEDIGBA S, et al. Dynamic data driven sonic well log model for formation evaluation[J]. Journal of Petroleum Science and Engineering, 2019, 175: 1049-1062. [本文引用:1]
[16] MAHMOUDABADI H, IZADI M, MENHAJ M B. A hybrid method for grade estimation using genetic algorithm and neural networks[J]. Computational Geosciences, 2009, 13: 91-101. [本文引用:1]
[17] 张东晓, 陈云天, 孟晋. 基于循环神经网络的测井曲线生成方法[J]. 石油勘探与开发, 2018, 45(4): 598-607.
ZHANG Dongxiao, CHEN Yuntian, MENG Jin. Synthetic well logs generation via Recurrent Neural Networks[J]. Petroleum Exploration and Development, 2018, 45(4): 598-607. [本文引用:1]
[18] 刘军, 钟洁, 倪振, 等. 基于机器学习的低含油饱和度砂岩储层参数预测: 以准噶尔盆地夏子街油田夏77井区下克拉玛依组为例[J]. 石油实验地质, 2024, 46(5): 1123-1134.
LIU Jun, ZHONG Jie, NI Zhen, et al. Machine learning-based prediction of low oil saturation sand stone reservoir parameters: a case study of Lower Karamay Formation in Xia 77 well block of Xiazijie Oilfield, Junggar Basin[J]. Petroleum Geology & Experiment, 2024, 46(5): 1123-1134. [本文引用:1]
[19] PUTRA M H R, Hermana M, SUANANDA YOGI I B, et al. Reservoir porosity assessment and anomaly identification from seismic attributes using Gaussian process machine learning[J]. Earth Science Informatics, 2024, 17(12): 1315-1327. [本文引用:1]
[20] HUSSAIN M, LIU S, HUSSAIN W, et al. Application of deep learning for reservoir porosity prediction and self organizing map for lithofacies prediction[J]. Journal of Applied Geophysics, 2024, 230(1): 105502. [本文引用:1]
[21] ZHOU H F, WANG X Q, ZHU R R. Feature selection based on mutual information with correlation coefficient[J]. Applied Intelligence, 2022, 52(5): 5457-5474. [本文引用:1]
[22] 邵蓉波, 肖立志, 廖广志, 等. 基于迁移学习的地球物理测井储层参数预测方法研究[J]. 地球物理学报, 2022, 65(2): 796-808.
SHAO Rongbo, XIAO Lizhi, LIAO Guangzhi, et al. A reservoir parameters prediction method for geophysical logs based on transfer learning[J]. Chinese Journal of Geophysics, 2022, 65(2): 796-808. [本文引用:1]
[23] SATTARZADEH A R, KUTADINATA R J, PATHIRANA P N, et al. A novel hybrid deep learning model with ARIMA Conv-LSTM networks and shuffle attention layer for short-term traffic flow prediction[J]. Transportmetrica A: Transport Science, 2025, 21(1, 2): 388-410. [本文引用:1]
[24] 白薷, 王世玉, 张璐, 等. 基于MAE神经网络的测井曲线地层自动识别方法[J]. 天然气勘探与开发, 2024, 47(4): 63-71.
BAI Ru, WANG Shiyu, ZHANG Lu, et al. An automatic identifying method for strata via logging curves based on MAE neural network[J]. Natural Gas Exploration and Development, 2024, 47(4): 63-71. [本文引用:1]
[25] 张益明, 张繁昌, 丁继才, 等. 基于混合深度学习网络的致密砂岩甜点预测[J]. 石油物探, 2021, 60(6): 995-1002.
ZHANG Yiming, ZHANG Fanchang, DING Jicai, et al. Sweet spot prediction in tight sand reservoirs by a hybrid deep-learning network[J]. Geophysical Prospecting for Petroleum, 2021, 60(6): 995-1002. [本文引用:1]