引用本文
张文颖, 毛敏, 袁胜斌. 基于蒙特卡洛半监督学习的录、测井流体识别方法[J]. 录井工程, 2025,36(4): 29-35.
ZHANG Wenying, MAO Min, YUAN Shengbin. Fluid identification method based on Monte Carlo semi-supervised learning for mud logging and well logging data[J]. Mud Logging Engineering, 2025,36(4): 29-35.
Doi:10.3969/j.issn.1672-9803.2025.04.005  
Permissions
Copyright©2025, 《录井工程》杂志社
《录井工程》杂志社 所有
基于蒙特卡洛半监督学习的录、测井流体识别方法
张文颖, 毛敏, 袁胜斌
中法渤海地质服务有限公司

作者简介：张文颖 工程师,1987年生,2011年毕业于中国石油大学（华东）固体地球物理学专业,现在中法渤海地质服务有限公司从事综合录井解释工作。通信地址：300457 天津市滨海新区开发区信环西路19号天河科技园1号楼7楼。E-mail：zhangwy@cfbgc.com

收稿日期: 2025-11-11
摘要

录、测井数据在储层流体识别,尤其是随钻阶段的流体识别中起着重要作用。录、测井数据体依赖于区域内井的数量,海上油气勘探在大数据维度上来说样本相对较少,导致在利用机器学习对储层流体进行识别时受限于有标签数据量太小,存在过拟合及泛化能力差等问题。针对上述问题,提出一种融合半监督学习（Self-Train）与马尔科夫链蒙特卡洛（MCMC）算法的流体识别方法。利用少量有标签数据初步训练神经网络模型;结合半监督学习算法为无标签数据生成机器标签（伪标签）,然后使用马尔科夫链蒙特卡洛法随机采样量化模型预测的不确定性,筛选置信度高的机器标签,以扩充高质量训练数据集,最终结合筛选后的机器标签与原有标签数据,采用自适应训练方法调整利用有标签数据建立的神经网络模型,构建适用于小样本条件的录、测井数据储层流体识别模型。对新钻井进行模型验证,符合率达到85%以上,应用效果较好。MCMC方法筛选机器标签后建立的储层识别模型,提升了随钻流体解释模型的准确率与泛化能力,为井场快速识别随钻流体提供了有效的技术支撑。

关键词: 马尔科夫链蒙特卡洛; 半监督学习; 小样本; 神经网络; 流体识别
中图分类号:TE132.1 文献标志码:A
Fluid identification method based on Monte Carlo semi-supervised learning for mud logging and well logging data
ZHANG Wenying, MAO Min, YUAN Shengbin
China France Bohai Geoservices Co., Ltd., Tianjin 300457, China
Abstract

Mud logging and well logging data play an important role in reservoir fluid identification, especially during the drilling stage. The data volumes of mud logging and well logging data depend on the number of wells in the area, and the number of samples is relatively small in terms of big data dimensions of offshore oil and gas exploration, which limits the machine learning of reservoir fluid identification due to the small amount of labeled data and leads to overfitting and poor generalization ability issues. To address the above problems, this paper proposes a fluid identification method that combines semi-supervised learning （Self-Train） with Markov Chain Monte Carlo （MCMC）. First, train the neural network model using a small amount of labeled data. Second, combining semi-supervised self learning algorithms to generate machine labels （pseudo labels） for unlabeled data. Then, using MCMC method to randomly sample and quantify the uncertainty predicted by the model, machine labels with high confidence coefficient are selected to expand the high-quality training dataset. Finally, by combining the screened machine tag with the original label data, and adopting adaptive training method to adjust and use the neural network model that is established with labeled data, a reservoir fluid identification model is created for mud logging and well logging data suitable for few-shot conditions. The model validation for new drilling wells achieved a coincidence rate of over 85%, demonstrating well application results. The reservoir identification model established after screening machine tags using the MCMC method improved the accuracy and generalization ability of the fluid interpretation model while drilling, providing effective technical support for rapid identification of fluids while drilling at the well site.

Keyword: Markov Chain Monte Carlo; semi-supervised learning; few-shot; neural network; fluid identification
0 引言

海上油气勘探受作业成本与施工难度制约, 油气钻井数量较少, 相对于大数据而言, 所获取的录、测井数据都属于小样本数据。随着勘探目标日趋复杂与勘探节奏不断加快, 对储层流体识别技术的智能化与实时性提出了更高要求。

传统的录、测井流体识别方法主要依赖气测、三维荧光、地化热解、电阻率、中子孔隙度等机理参数及其衍生参数, 通过建立区域评价图板与标准进行流体性质判定。然而, 此类常规方法对录、测井数据在多维空间中的复杂关联性考虑不足, 难以充分挖掘数据潜力。尽管神经网络在诸多领域取得显著成效, 但其依赖大数据, 应用效果取决于大量带类标签的训练样本。在录、测井流体识别领域, 由于数据匮乏, 没有足够的类标签训练, 容易导致神经网络模型在训练过程中出现过拟合、泛化能力弱的问题, 往往模型准确率高, 但是应用效果差, 制约了神经网络的广泛应用。

半监督学习作为一种能够同时利用少量标签数据与大量无标签数据的技术, 已成为当前研究的热点, 其核心在于通过算法为无标签数据生成机器标签（伪标签）, 以扩充训练集。如何评估并筛选出高置信度的伪标签, 是提升模型性能的关键。与此同时, 马尔科夫链蒙特卡洛（MCMC）法在量化预测不确定性方面展现出强大能力, 在石油勘探领域已被广泛应用于岩石物理反演与地质建模, 以解决反演的不确定性问题。赵林[1]利用MCMC方法的全局最优化技术进行地质统计学求解, 用稳定的模型反演出空间上的波阻抗体及岩性体; 王丹阳[2]利用MCMC方法反演得到大量来自于后验概率分布的样本, 获得每个未知参数的估计值和与之相关的各种不确定性信息; 潘新朋[3]、周爽爽等[4]、Zhang等[5]都利用MCMC方法对岩石物理反演进行优化和改进; 张新生等[6]将MCMC方法应用到数据融合, 预测腐蚀油气管道剩余寿命; Luu等[7]用自适应核密度估计法建立与深度相关的钻井周期概率模型, 结合MCMC方法模拟得出钻完井总周期的概率分布; 王丽芳等[8]采用基于贝叶斯-马尔科夫链MCMC方法的三维地质模型概率性推断框架, 嵌入已有地质知识或地球物理勘探数据, 实现数据和知识融合的三维地质建模; 冉飞飞等[9]将MCMC方法应用到海上井光纤监测中, 构建海上大位移注水井DTS数据反演模型, 实现了注水剖面的定量解释。

探索一种有效结合不确定性量化的半监督学习框架, 对于解决实际生产中的小样本流体识别难题具有重要意义。本文充分利用无标签数据, 结合半监督学习算法生成初始机器标签, 再利用蒙特卡洛随机采样量化模型预测的不确定性筛选置信度高的机器标签, 利用有标签数据和筛选出来的机器标签调整初始神经网络模型, 以期得到更准确的解释模型, 增强模型的泛化能力, 为海上油气田的随钻解释与快速决策提供可靠的技术支持。

1 录、测井解释学习算法
1.1 半监督学习算法

半监督学习是一种机器学习方法, 与有标签和无标签数据的学习过程结合, 特别适用于有标签数据稀缺但无标签数据丰富的情况。本研究采用的半监督学习旨在解决录、测井解释中有标签数据稀缺的核心难题。

在初期阶段使用研究区内有限的、带有准确流体结论（如油层、气层、水层等）的有标签数据, 通过训练一个初始神经网络模型, 利用这些有标签数据中的已知信息来捕捉关键的地质特征和录、测井响应模式。在基础模型的初步训练完成后, 将大量无标签的录、测井数据输入到上述模型中, 通过半监督学习机制来扩展模型的学习范围, 并为这些数据打上机器标签（即伪标签）。然而, 由初始模型生成的伪标签不可避免地包含噪声, 直接将其加入训练集可能误导模型, 导致性能下降。为此, 引入马尔科夫链蒙特卡洛法对伪标签进行不确定性量化与筛选。

1.2 马尔科夫链蒙特卡洛法

马尔科夫链蒙特卡洛法是一种基于贝叶斯理论的随机采样方法, 其核心思想是构建平稳分布的马尔科夫链, 然后基于该链进行随机游走而产生样本的序列（也就是抽样）, 再进行近似数值计算不确定性, 最终通过链的遍历样本进行蒙特卡洛积分[10]。在实际应用中, 由于权重空间通常非常大, 该积分无法直接计算。蒙特卡洛丢弃（MC dropout）法通常用于处理解析解难以求取或者无法求得的复杂积分问题, 采用丢弃的方式来避免过拟合, 是实现贝叶斯神经网络不确定性估计的一种高效近似方法[11]。该方法将权重应用于输入层, 以概率方式将部分神经元从隐藏层中丢弃, 可降低模型的复杂度, 因而蒙特卡洛丢弃法更容易应对未见过的输入, 在半监督学习过程中能更好地泛化模型。

蒙特卡洛丢弃法的核心是预测分布, 公式如下：

q（y* x* ）=∫p（y* x* ，ω）q（ω）dω（1）

式中：x* 为需要进行预测的数据集; y* 为期望得到的输出; ω 为权重（是随机变量）; q（y* x* ）为输入x* 后y* 的概率分布; 右侧积分表示对所有可能的权重ω 分布 q（ω）进行积分, 计算条件概率 p（y* x* ，ω）的期望; p（y* x* ，ω）为条件概率, 表示输入x* 在模型权重为ω 的情况下输出y* 的分布。

蒙特卡洛丢弃法通过对初期建立的神经网络模型进行多次正向传播, 每次传播时随机丢弃网络中的一些神经元, 模拟 q（ω）并得到不同的输出结果, 然后用多次传播的结果求平均来近似这个积分, 进而得到y* 的预测分布。近似计算预测输出的期望 Eq（y* x* ）（y* ）如下：

Eq（y* x* ）（y* ）≈1T∑t=1Tŷ* （x* ，W1t，W2t，…，WLt）（2）

式中：T为采样次数, 即正向传播次数; t为第t次正向传播, t=1, 2, …, T; L为数据集参数的个数; WLt为第t次正向传播时, 第L个参数由于丢弃而随机生成的权重矩阵; 公式右侧表示T次不同的丢弃实验结果 ŷ* （x* ，W1t，W2t，…，WLt）的平均值, 其中每一项表示在第t次正向预测时, 丢弃权重过后对x* 的预测输出, 对这些结果求平均得到对应的期望。

蒙特卡洛丢弃法通过多次随机关闭神经网络的单元（丢弃部分神经元）模拟不确定性, 多次采样平均近似得到输出的预测分布, 最终以其与预测结果的偏差来量化模型对数据预测的不确定性。MCMC方法可以对一个数据（机器标签）反复预测多次, 每一次预测都会对每个机器标签有一个置信度的分数, 多次置信度分数方差小或者多次预测结论一致的机器标签即为确信的机器标签。有效的标签数据扩充后, 有足够的样本进行机器学习, 提升模型的准确性与泛化能力。

2 利用BP神经网络建立随钻流体识别模型

BP神经网络通过模拟人脑神经元的连接模式, 对已有数据进行多次训练, 建立特定的学习规则, 得到神经网络模型。输入新的数据时通过模型可以预测出最接近期望的输出值[12]。本研究基于西湖凹陷区域录、测井资料, 采用无标签数据扩充方式, 结合神经网络理论, 建立录、测井流体识别模型。从扩充后的标签数据中优选了包括气测组分、电阻率、孔隙度等在内的28个对流体响应敏感的录、测井参数作为模型输入, 输出结果为5类流体类型, 即油层、气层、气水同层、含气水层、水干层。

BP神经网络基于梯度下降法, 利用梯度搜索技术, 使网络的实际输出值和期望输出值的均方差误差为最小。BP神经网络模型包含输入层、隐藏层和输出层, 计算过程包括正向计算和反向计算[13]。正向传播是从输入层经隐藏层逐层处理, 并转向输出层, 每一层神经元的状态只影响下一层神经元的状态。如果输出层没有达到期望的输出, 则误差信号沿原来的连接通路返回, 转入到反向传播, 进而修改各神经元的权值, 将误差降低到最小。为了用矩阵乘法更清晰地表示该网络的预测过程, 设输入数据为X, 权重矩阵分别为W1、W2, 偏置向量为b1、b2, 激活函数为f, 最终预测输出为y。对于研究数据来说, 输入数据的维度为28, 输出数据的维度为5。

第一层（输入层到隐藏层）：输入维度28, 输出维度25, 即权重矩阵W1维度为28× 25; 运算表示h1=f（W1TX+b1）, 其中h1为第一层输出, 维度为1× 25;

第二层（隐藏层到输出层）：输入维度25, 输出维度5, 即权重矩阵W2维度为25× 5; 运算表示为y=W2Th1+b2, 其中y为第二层输出, 维度为1× 5。

整个神经网络预测过程为y=W2T[f（W1TX+b1）]+b2, 其中激活函数为f=max（x, 0）。

训练过程中, 使用标签扩充后的数据, 将录、测井参数作为模型输入, 并将有标签数据解释结论与1.2节中筛选后的机器标签解释结论作为模型输出（即5种流体类型）, 进行BP神经网络训练。多次训练后, 最终选取均方差误差小、预测结果与原结果相似系数最高的模型作为随钻录、测井数据储层流体识别模型。

3 实钻井应用效果
3.1 训练模型验证效果

西湖凹陷中深层录、测井数据及解释结论的有标签数据271条, 无标签数据61条, 为验证上述方法的有效性, 随机抽取有标签数据80%的数据作为训练集, 其余20%作为测试集, 分别建立基础神经网络模型与引入经MCMC标签增强的模型并进行对比, 最终将模型应用到全集数据中。表1展示了部分井模型输入的录、测井数据, 直接机器标签（仅使用原始有标签数据训练神经网络得到）和MCMC筛选后的机器标签（经无标签数据扩充后得到）, 结果显示, 直接机器标签在的解释结论一致率为75.65%（205/271）, 而引入经MCMC筛选的高置信度机器标签后, MCMC标签增强后模型的一致率显著提升至85.61%（232/271）。充分证明了MCMC筛选对于提升伪标签质量、增强模型泛化能力的关键作用。

表1 模型录测数据、直接机器标签和MCMC筛选后机器标签对比（部分井数据）

为直观对比传统方法、基础神经网络模型、MCMC标签增强模型的流体识别效果, 将高维空间数据降维转换成二维图板（降维后横、纵坐标没有对应的物理量, 以特征值进行标注）。传统解释图板是基于优选的关键录、测井参数直接绘制的二维图板, 如图1a所示, 5种流体类型数据点相互混杂, 很难区分。采用基础神经网络模型后水干层、含气水层和气水同层能够大致区分, 但是油层、气层叠置较多（图1b）, 与测井解释结论符合率达到75.65%。通过MCMC随机采样量化模型增强训练后, 能够区分水干层、含气水层和气水同层, 气层和油层叠置情况也有所改善, 与测井解释结论符合率达到85.61%（图1c）。通过图板对比可以看出, MCMC标签增强后的模型, 油层、气层和含气水层解释结论更聚焦, 与测井解释一致率得到提高, 便于后续新井随钻解释进行流体识别。

图1 西湖凹陷流体识别解释图板效果对比

3.2 新钻井应用效果

为检验模型的泛化能力, 分别对西湖凹陷和黄河口凹陷两口新钻井（A、B井）进行了验证。

3.2.1 A井验证

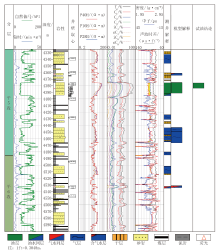
在西湖凹陷新钻井A井的验证中（图2）, 模型对平湖组共计14个解释层段进行了预测, 其中12个层段的解释结论与测井解释一致, 符合率达到86%。平湖组平5段4 375~4 395 m砂岩段, 测井解释为油层, 模型解释为油层, 试油结论证实为油层, 与试油结论完全符合; 平5段4 442~4 466 m井段, 测井解释为水层（扣除两个薄层干层）, 模型解释为水层; 平6段4 532~4 534 m井段, 测井解释为气水同层, 模型解释结果一致, 证实了其实际应用的有效性。

图2 西湖凹陷新钻井A井验证

3.2.2 B井验证

在黄河口凹陷新钻井B井验证中（图3）, 模型对沙河街组 9个解释层段进行了预测, 与测井解释一致的层段为8个, 符合率高达89%。沙河街组沙二段3 727~3 729 m测井解释为干层, 模型解释为干层; 沙三段3 790~3 793 m、3 813~3 813.8 m、3 823~3 824 m、3 835~3 837 m四处薄层测井与模型均解释为干层; 沙三段3 850~3 855 m砂岩段, 测井解释为油层（底部为干层）, 模型解释为油层, 电缆测试为油层, 与电缆测试结论一致, 证实了其实际应用的有效性。

图3 黄河口凹陷新钻井B井验证

4 结论

（1）本文先利用已有标签数据集训练, 建立神经网络模型, 结合半监督学习算法为无标签数据打上机器标签, 进一步应用蒙特卡洛方法从机器标签数据中筛选出置信度高的标签, 样本数增加后再进行神经网络学习, 准确率得到有效提升, 从最初的75.65%提升到85.61%。对西湖凹陷和黄河口凹陷两口新钻井验证, 与试油结论或电缆测试结果完全一致, 与测井解释一致率达到85%以上。

（2）MCMC方法结合神经网络学习针对无标签数据可以提升标签数据样本量, 在一定程度上解决了录、测井小样本数据的难题, 增强了最终模型的泛化能力, 在随钻过程中取得了较好的应用效果。

（3）半监督学习建立的解释模型可移植性强, 减少人工分析和干预, 依据不同的样本集可以快速建立目标区域的解释模型。

（4）由于机器学习严重依赖于样本数量, 当勘探井数增加、样本数量增多时, 可将数据加入并更新模型, 增强机器学习的能力。

（编辑 卜丽媛）

参考文献
[1] 赵林. 马尔可夫链蒙特卡罗模拟在储层反演中的应用[J]. 石油与天然气学报, 2010, 32(2): 249-252, 266.
ZHAO Lin. Application of Monte Carlo simulation of Markov Chain in seismic inversion[J]. Journal of Oil and Gas Technology, 2010, 32(2): 249-252, 266. [本文引用:1]
[2] 王丹阳. 基于MCMC方法的叠前反演方法研究[D]. 青岛: 中国石油大学(华东), 2012.
WANG Danyang. Research on pre-stack inversion method based on MCMC method[D]. Qingdao: China University of Petroleum (East China), 2012. [本文引用:1]
[3] 潘新朋. 优化MCMC方法在地震反演中的应用研究[D]. 青岛: 中国石油大学(华东), 2016.
PAN Xinpeng. Application of optimized MCMC method in seismic inversion[D]. Qingdao: China University of Petroleum (East China), 2016. [本文引用:1]
[4] 周爽爽, 印兴耀, 裴松, 等. 地震波形约束的蒙特卡洛-马尔科夫链随机反演方法[J]. 石油地球物理勘探, 2021, 56(3): 543-554.
ZHOU Shuangshuang, YIN Xingyao, PEI Song, et al. A Monte Carlo-Markov chain stochastic inversion method with seismic waveform constraints[J]. Oil Geophysical Prospecting, 2021, 56(3): 543-554. [本文引用:1]
[5] ZHANG J J, LI H B, ZHANG G Z, et al. Rock physics invervsion based on an optimized MCMC method[J]. Applied Geophysics, 2021, 18(3): 288-298. [本文引用:1]
[6] 张新生, 吕品品, 王明虎, 等. 数据融合下的腐蚀油气管道剩余寿命预测[J]. 材料保护, 2018, 51(10): 59-65.
ZHANG Xinsheng, LYU Pinpin, WANG Minghu, et al. Residual lifetime prediction of corroded pipelines based on data fusion[J]. Materials Protection, 2018, 51(10): 59-65. [本文引用:1]
[7] LUU Quang Hung, LAU Man Fai, NG Sebastian P. H. , 等. 基于多变量概率模型的钻井周期预测方法[J]. 石油勘探与开发, 2021, 48(4): 851-860.
LUU Quang Hung, LAU Man Fai, NG Sebastian P. H. , et al. Predictability of well construction time with multivariate probabilistic approach[J]. Petroleum Exploration and Development, 2021, 48(4): 851-860. [本文引用:1]
[8] 王丽芳, 刘肖莉, 徐坤, 等. 数据和知识融合的Bayesian-MCMC三维地质建模[J]. 地球科学, 2024, 49(8): 3056-3070.
WANG Lifang, LIU Xiaoli, XU Kun, et al. Bayesian-MCMC(Markov Chain Monte Carlo)Based three-dimensional geological model optimization by data and knowledge fusion[J]. Earth Science, 2024, 49(8): 3056-3070. [本文引用:1]
[9] 冉飞飞, 罗红文, 李颖, 等. 海上大位移井注水剖面光纤监测反演方法[J]. 测井技术, 2025, 49(4): 519-530.
RAN Feifei, LUO Hongwen, LI Ying, et al. Inversion method for fiber-optic monitoring of water injection profiles in offshore extended-reach wells[J]. Well Logging Technology, 2025, 49(4): 519-530. [本文引用:1]
[10] 朱新玲. 马尔科夫链蒙特卡罗方法研究综述[J]. 统计与决策, 2009(21): 151-153.
ZHU Xinling. A review of research on Markov Chain Monte Carlo method[J]. Statistics & Decision, 2009(21): 151-153. [本文引用:1]
[11] 史会峰, 谷根代, 姜波. 基于MCMC算法贝叶斯网络的学习[J]. 华北电力大学学报, 2004, 31(4): 109-112.
SHI Huifeng, GU Gendai, JIANG Bo. Learning of Bayesian network based on MCMC algorithm[J]. Journal of North China Electric Power University, 2004, 31(4): 109-112. [本文引用:1]
[12] 张文颖, 袁胜斌, 陈伟, 等. BP神经网络模型在元素-矿物转换中的应用[J]. 录井工程, 2023, 34(3): 1-6.
ZHANG Wenying, YUAN Shengbin, CHEN Wei, et al. Application of BP neural network model in element-mineral conversion[J]. Mud Logging Engineering, 2023, 34(3): 1-6. [本文引用:1]
[13] 王娜娜. 神经网络在测井岩性识别中的应用[D]. 北京: 北京化工大学, 2009.
WANG Nana. Application of neural network in logging lithology identification[D]. Beijing: Beijing University of Chemical Technology, 2009. [本文引用:1]